Menu Close

Question-43699

Tinku Tara 0 Comments
Pin




Question Number 43699 by Meritguide1234 last updated on 14/Sep/18
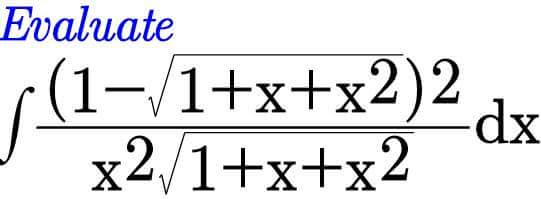
Commented by Meritguide1234 last updated on 14/Sep/18
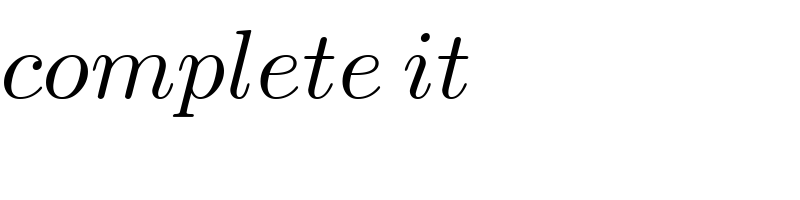
complete it
$${complete}\:{it} \\ $$
Commented by maxmathsup by imad last updated on 14/Sep/18
let I = ∫ (((1−(√(1+x+x^2 )))^2 )/(x^2 (√(1+x+x^2 ))))dx we have I= ∫ ((1−2(√(1+x+x^2 ))+1+x+x^2 )/(x^2 (√(1+x+x^2 ))))dx = ∫ (dx/(x^2 (√(1+x+x^2 ))))dx −2 ∫ (dx/x^2 ) + ∫ ((√(1+x+x^2 ))/x^2 )dx but −2 ∫ (dx/x^2 ) =(2/x) +c and ∫ (dx/(x^2 (√(1+x+x^2 )))) = ∫ (dx/(x^2 (√((x+(1/2))^2 +(3/4))))) =_(x+(1/2)=((√3)/2)sh(t)) ∫ (1/((((√3)/2)sh(t)−(1/2))^2 ((√3)/2)ch(t))) ((√3)/2) ch(t)dt = ∫ ((4dt)/(((√3)sh(t)−1)^2 )) = ∫ ((4dt)/(3sh^2 (t)−2(√3)sh(t) +1)) = ∫ ((4dt)/(3((1+ch(2t))/2)−2(√3)sh(t)+1)) =8 ∫ (dt/(3 +3ch(2t)−4(√3)sh(t) +2)) =8 ∫ (dt/(3 +3 ((e^(2t) +e^(−2t) )/2) −4(√3)((e^t −e^(−t) )/2)+2)) =16 ∫ (dt/(6 +3 e^(2t) +3e^(−2t) −4(√3)e^t +4(√3)e^(−t) +4)) =_(e^t =u) 16 ∫ (du/(u{ 10 +3u^2 +3u^(−2) −4(√3)u +4(√3)u^(−1) })) =16 ∫ (du/(10u +3u^3 +3u^(−1) −4(√3)u^2 +4(√3))) =16 ∫ ((udu)/(10u^2 +3u^(4 ) +3 −4(√3)u^3 +4(√3)u )) let decompose F(u) = (u/(3u^4 −4(√3)u^3 +10u^2 +4(√3)u +3)) ...be continued...
$${let}\:{I}\:=\:\int\:\:\frac{\left(\mathrm{1}−\sqrt{\mathrm{1}+{x}+{x}^{\mathrm{2}} }\right)^{\mathrm{2}} }{{x}^{\mathrm{2}} \sqrt{\mathrm{1}+{x}+{x}^{\mathrm{2}} }}{dx}\:\:{we}\:{have}\:\:{I}=\:\int\:\frac{\mathrm{1}−\mathrm{2}\sqrt{\mathrm{1}+{x}+{x}^{\mathrm{2}} }+\mathrm{1}+{x}+{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} \sqrt{\mathrm{1}+{x}+{x}^{\mathrm{2}} }}{dx} \\ $$$$=\:\int\:\:\:\frac{{dx}}{{x}^{\mathrm{2}} \sqrt{\mathrm{1}+{x}+{x}^{\mathrm{2}} }}{dx}\:−\mathrm{2}\:\int\:\:\frac{{dx}}{{x}^{\mathrm{2}} }\:\:\:+\:\int\:\:\:\frac{\sqrt{\mathrm{1}+{x}+{x}^{\mathrm{2}} }}{{x}^{\mathrm{2}} }{dx}\:\:{but} \\ $$$$−\mathrm{2}\:\int\:\frac{{dx}}{{x}^{\mathrm{2}} }\:=\frac{\mathrm{2}}{{x}}\:+{c}\:\:\:{and}\:\:\int\:\:\:\:\:\frac{{dx}}{{x}^{\mathrm{2}} \sqrt{\mathrm{1}+{x}+{x}^{\mathrm{2}} }}\:=\:\int\:\:\:\frac{{dx}}{{x}^{\mathrm{2}} \sqrt{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{4}}}} \\ $$$$=_{{x}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{sh}\left({t}\right)} \:\:\:\:\int\:\:\:\:\:\frac{\mathrm{1}}{\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{sh}\left({t}\right)−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{ch}\left({t}\right)}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:{ch}\left({t}\right){dt} \\ $$$$=\:\int\:\:\:\:\:\frac{\mathrm{4}{dt}}{\left(\sqrt{\mathrm{3}}{sh}\left({t}\right)−\mathrm{1}\right)^{\mathrm{2}} }\:=\:\int\:\:\:\:\:\frac{\mathrm{4}{dt}}{\mathrm{3}{sh}^{\mathrm{2}} \left({t}\right)−\mathrm{2}\sqrt{\mathrm{3}}{sh}\left({t}\right)\:+\mathrm{1}} \\ $$$$=\:\int\:\:\:\:\:\frac{\mathrm{4}{dt}}{\mathrm{3}\frac{\mathrm{1}+{ch}\left(\mathrm{2}{t}\right)}{\mathrm{2}}−\mathrm{2}\sqrt{\mathrm{3}}{sh}\left({t}\right)+\mathrm{1}}\:=\mathrm{8}\:\int\:\:\:\:\frac{{dt}}{\mathrm{3}\:+\mathrm{3}{ch}\left(\mathrm{2}{t}\right)−\mathrm{4}\sqrt{\mathrm{3}}{sh}\left({t}\right)\:+\mathrm{2}} \\ $$$$=\mathrm{8}\:\int\:\:\:\:\frac{{dt}}{\mathrm{3}\:+\mathrm{3}\:\frac{{e}^{\mathrm{2}{t}} \:+{e}^{−\mathrm{2}{t}} }{\mathrm{2}}\:−\mathrm{4}\sqrt{\mathrm{3}}\frac{{e}^{{t}} \:−{e}^{−{t}} }{\mathrm{2}}+\mathrm{2}}\:=\mathrm{16}\:\int\:\:\:\:\:\frac{{dt}}{\mathrm{6}\:+\mathrm{3}\:{e}^{\mathrm{2}{t}} \:+\mathrm{3}{e}^{−\mathrm{2}{t}} \:−\mathrm{4}\sqrt{\mathrm{3}}{e}^{{t}} +\mathrm{4}\sqrt{\mathrm{3}}{e}^{−{t}} +\mathrm{4}} \\ $$$$=_{{e}^{{t}} \:={u}} \:\:\:\:\mathrm{16}\:\:\int\:\:\:\:\:\:\:\frac{{du}}{{u}\left\{\:\mathrm{10}\:+\mathrm{3}{u}^{\mathrm{2}} \:+\mathrm{3}{u}^{−\mathrm{2}} \:−\mathrm{4}\sqrt{\mathrm{3}}{u}\:+\mathrm{4}\sqrt{\mathrm{3}}{u}^{−\mathrm{1}} \right\}} \\ $$$$=\mathrm{16}\:\int\:\:\frac{{du}}{\mathrm{10}{u}\:+\mathrm{3}{u}^{\mathrm{3}} \:+\mathrm{3}{u}^{−\mathrm{1}} \:−\mathrm{4}\sqrt{\mathrm{3}}{u}^{\mathrm{2}} \:+\mathrm{4}\sqrt{\mathrm{3}}} \\ $$$$=\mathrm{16}\:\int\:\:\:\frac{{udu}}{\mathrm{10}{u}^{\mathrm{2}} \:+\mathrm{3}{u}^{\mathrm{4}\:} \:+\mathrm{3}\:−\mathrm{4}\sqrt{\mathrm{3}}{u}^{\mathrm{3}} \:+\mathrm{4}\sqrt{\mathrm{3}}{u}\:}\:\:{let}\:{decompose} \\ $$$${F}\left({u}\right)\:=\:\frac{{u}}{\mathrm{3}{u}^{\mathrm{4}} \:−\mathrm{4}\sqrt{\mathrm{3}}{u}^{\mathrm{3}} \:+\mathrm{10}{u}^{\mathrm{2}} \:+\mathrm{4}\sqrt{\mathrm{3}}{u}\:+\mathrm{3}}\:\:…{be}\:{continued}… \\ $$
Commented by MJS last updated on 14/Sep/18
there′s a magic word and I seem to remember it starts with “p”.
$$\mathrm{there}'\mathrm{s}\:\mathrm{a}\:\mathrm{magic}\:\mathrm{word}\:\mathrm{and}\:\mathrm{I}\:\mathrm{seem}\:\mathrm{to}\:\mathrm{remember} \\ $$$$\mathrm{it}\:\mathrm{starts}\:\mathrm{with}\:“\mathrm{p}''. \\ $$
Commented by Meritguide1234 last updated on 15/Sep/18
Answered by tanmay.chaudhury50@gmail.com last updated on 14/Sep/18
∫((1−2(√(1+x+x^2 )) +1+x+x^2 )/(x^2 (√(1+x+x^2 )) ))dx ∫(dx/(x^2 (√(1+x+x^2 )) ))−2∫(dx/x^2 )+∫(((√(1+x+x^2 )) )/x^2 )dx I=I_1 −2I_2 +I_3 I_1 =∫(dx/(x^2 (√(1+x+x^2 )) )) t=(1/x)dx dt=−(dx/x^2 ) ∫((−dt)/( (√(1+(1/t)+(1/t^2 ))))) ∫((−tdt)/( (√(t^2 +t+1))))(/) ((−1)/2)∫((2t+1−1)/( (√(t^2 +t+1))))dt =(1/2)∫(dt/( (√(t^2 +t+1))))−(1/2)∫((d(t^2 +t+1))/( (√(t^2 +t+1)))) =(1/2)∫(dt/( (√(t^2 +2.t.(1/2)+(1/4)+1−(1/4)))))−(1/2)∫((d(t^2 +t+1))/( (√(t^2 +t+1))))dt =(1/2)∫(dt/( (√((t+(1/2))^2 +((((√3) )/2))^2 ))))−(1/2)∫((d(t^2 +t+1))/( (√(t^2 +t+1)))) =(1/2)ln{(t+(1/2))+(√(t^2 +t+1)) }−(1/2)×((√(t^2 +t+1))/(1/2)) =(1/2)ln{(t+(1/2))+(√(t^2 +t+1)) }−(√(t^2 +t+1)) =(1/2)ln{((1/x)+(1/2))+(√((1/x^2 )+(1/x)+1)) }−(√((1/x^2 )+(1/x)+1)) I_2 =∫(dx/x^2 )=(x^(−1) /(−1))=((−1)/x) I_3 =∫((√(1+x+x^2 ))/x^2 ) =∫((1+x+x^2 )/(x^2 (√(1+x+x^2 ))))dx =∫(dx/(x^2 (√(1+x+x^2 ))))+∫(dx/(x(√(1+x+x^2 )) ))+∫(dx/( (√(1+x+x^2 )))) =same as I_1 +∫(dx/(x(√(1+x+x^2 ))))+∫(dx/( (√((x+(1/2))^2 +(((√3)/2))^2 )))) =same as I_1 +ln{(x+(1/2))+(√(x^2 +x+1)) }+∫(dx/(x(√(1+x+x^2 )))) =(1/2)ln{((1/x)+(1/2))+(√((1/x^2 )+(1/x)+1)) }−(√((1/x^2 )+(1/x)+1)) + ln{(x+(1/2)+(√(x^2 +x+1)) }+∫(dx/(x(√(1+x+x^2 )))) ∫(dx/(x(√(1+x+x^2 )))) x=(1/t) dx=((−1)/t^2 )dt ∫((−dt)/(t^2 ×(1/t)×(√(1+(1/t)+(1/t^2 ))))) ∫((−dt)/( (√(t^2 +t+1)))) =−ln{t+(1/2))+(√(t^2 +t+1)) } =−ln[((1/x)+(1/2))+{(√((1/x^2 )+(1/x)+1))}] NOW PLS put the value of I_1 −2I_2 +I_3
$$\int\frac{\mathrm{1}−\mathrm{2}\sqrt{\mathrm{1}+{x}+{x}^{\mathrm{2}} }\:\:+\mathrm{1}+{x}+{x}^{\mathrm{2}} \:}{{x}^{\mathrm{2}} \sqrt{\mathrm{1}+{x}+{x}^{\mathrm{2}} }\:}{dx} \\ $$$$\int\frac{{dx}}{{x}^{\mathrm{2}} \sqrt{\mathrm{1}+{x}+{x}^{\mathrm{2}} }\:}−\mathrm{2}\int\frac{{dx}}{{x}^{\mathrm{2}} }+\int\frac{\sqrt{\mathrm{1}+{x}+{x}^{\mathrm{2}} }\:}{{x}^{\mathrm{2}} }{dx} \\ $$$${I}={I}_{\mathrm{1}} −\mathrm{2}{I}_{\mathrm{2}} +{I}_{\mathrm{3}} \\ $$$${I}_{\mathrm{1}} =\int\frac{{dx}}{{x}^{\mathrm{2}} \sqrt{\mathrm{1}+{x}+{x}^{\mathrm{2}} }\:} \\ $$$${t}=\frac{\mathrm{1}}{{x}}{dx} \\ $$$${dt}=−\frac{{dx}}{{x}^{\mathrm{2}} } \\ $$$$\int\frac{−{dt}}{\:\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{t}}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}} \\ $$$$\int\frac{−{tdt}}{\:\sqrt{{t}^{\mathrm{2}} +{t}+\mathrm{1}}}\frac{}{} \\ $$$$\frac{−\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{t}+\mathrm{1}−\mathrm{1}}{\:\sqrt{{t}^{\mathrm{2}} +{t}+\mathrm{1}}}{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dt}}{\:\sqrt{{t}^{\mathrm{2}} +{t}+\mathrm{1}}}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({t}^{\mathrm{2}} +{t}+\mathrm{1}\right)}{\:\sqrt{{t}^{\mathrm{2}} +{t}+\mathrm{1}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dt}}{\:\sqrt{{t}^{\mathrm{2}} +\mathrm{2}.{t}.\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}}}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({t}^{\mathrm{2}} +{t}+\mathrm{1}\right)}{\:\sqrt{{t}^{\mathrm{2}} +{t}+\mathrm{1}}}{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dt}}{\:\sqrt{\left({t}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}\:}{\mathrm{2}}\right)^{\mathrm{2}} }}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({t}^{\mathrm{2}} +{t}+\mathrm{1}\right)}{\:\sqrt{{t}^{\mathrm{2}} +{t}+\mathrm{1}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left\{\left({t}+\frac{\mathrm{1}}{\mathrm{2}}\right)+\sqrt{{t}^{\mathrm{2}} +{t}+\mathrm{1}}\:\right\}−\frac{\mathrm{1}}{\mathrm{2}}×\frac{\sqrt{{t}^{\mathrm{2}} +{t}+\mathrm{1}}}{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left\{\left({t}+\frac{\mathrm{1}}{\mathrm{2}}\right)+\sqrt{{t}^{\mathrm{2}} +{t}+\mathrm{1}}\:\right\}−\sqrt{{t}^{\mathrm{2}} +{t}+\mathrm{1}}\: \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left\{\left(\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{\mathrm{2}}\right)+\sqrt{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{{x}}+\mathrm{1}}\:\:\right\}−\sqrt{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{{x}}+\mathrm{1}}\: \\ $$$${I}_{\mathrm{2}} =\int\frac{{dx}}{{x}^{\mathrm{2}} }=\frac{{x}^{−\mathrm{1}} }{−\mathrm{1}}=\frac{−\mathrm{1}}{{x}} \\ $$$${I}_{\mathrm{3}} =\int\frac{\sqrt{\mathrm{1}+{x}+{x}^{\mathrm{2}} }}{{x}^{\mathrm{2}} } \\ $$$$=\int\frac{\mathrm{1}+{x}+{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} \sqrt{\mathrm{1}+{x}+{x}^{\mathrm{2}} }}{dx} \\ $$$$=\int\frac{{dx}}{{x}^{\mathrm{2}} \sqrt{\mathrm{1}+{x}+{x}^{\mathrm{2}} \:}}+\int\frac{{dx}}{{x}\sqrt{\mathrm{1}+{x}+{x}^{\mathrm{2}} }\:}+\int\frac{{dx}}{\:\sqrt{\mathrm{1}+{x}+{x}^{\mathrm{2}} }} \\ $$$$={same}\:{as}\:{I}_{\mathrm{1}} +\int\frac{{dx}}{{x}\sqrt{\mathrm{1}+{x}+{x}^{\mathrm{2}} }}+\int\frac{{dx}}{\:\sqrt{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} }} \\ $$$$={same}\:{as}\:{I}_{\mathrm{1}} +{ln}\left\{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)+\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\:\right\}+\int\frac{{dx}}{{x}\sqrt{\mathrm{1}+{x}+{x}^{\mathrm{2}} }} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left\{\left(\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{\mathrm{2}}\right)+\sqrt{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{{x}}+\mathrm{1}}\:\:\right\}−\sqrt{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{{x}}+\mathrm{1}}\:+ \\ $$$${ln}\left\{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\:\right\}+\int\frac{{dx}}{{x}\sqrt{\mathrm{1}+{x}+{x}^{\mathrm{2}} }}\right. \\ $$$$\int\frac{{dx}}{{x}\sqrt{\mathrm{1}+{x}+{x}^{\mathrm{2}} \:}} \\ $$$${x}=\frac{\mathrm{1}}{{t}}\:\:{dx}=\frac{−\mathrm{1}}{{t}^{\mathrm{2}} }{dt} \\ $$$$\int\frac{−{dt}}{{t}^{\mathrm{2}} ×\frac{\mathrm{1}}{{t}}×\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{t}}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}} \\ $$$$\int\frac{−{dt}}{\:\sqrt{{t}^{\mathrm{2}} +{t}+\mathrm{1}}} \\ $$$$\left.=−{ln}\left\{{t}+\frac{\mathrm{1}}{\mathrm{2}}\right)+\sqrt{{t}^{\mathrm{2}} +{t}+\mathrm{1}}\:\right\} \\ $$$$=−{ln}\left[\left(\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{\mathrm{2}}\right)+\left\{\sqrt{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{{x}}+\mathrm{1}}\right\}\right] \\ $$$$\boldsymbol{{N}}{OW}\:{PLS}\:{put}\:{the}\:{value}\:{of}\:{I}_{\mathrm{1}} −\mathrm{2}{I}_{\mathrm{2}} +{I}_{\mathrm{3}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *