Question Number 43728 by Cheyboy last updated on 14/Sep/18
Commented by A.Haq.Soomro last updated on 15/Sep/18

$$\mathrm{See}\:\mathrm{Q}#\mathrm{6852} \\ $$
Answered by MrW3 last updated on 16/Sep/18
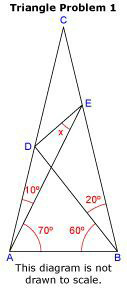
![let AB=1 ((AE)/(sin 80°))=((AB)/(sin 30°)) ⇒AE=((sin 80°)/(sin 30°))×AB=2 sin 80°=2 cos 10° ((BD)/(sin 80°))=((AB)/(sin 40°)) ⇒BD=((sin 80°)/(sin 40°))×AB=2 cos 40° ((BE)/(sin 70°))=((AB)/(sin 30°)) ⇒BE=((sin 70°)/(sin 30°))×AB=2 sin 70°=2 cos 20° DE^2 =BD^2 +BE^2 −2×BD×BE×cos 20° =4 cos^2 40°+ 4 cos^2 20°−8 cos 40° cos 20° cos 20^2 =4 (cos^2 40°+ cos^2 20°−2 cos 40° cos^2 20°) =4 [(2 cos^2 20°−1)^2 + cos^2 20°−2 (2×cos^2 20°−1) cos^2 20°] =4 [4 cos^4 20°−4 cos^2 20°+1+ cos^2 20°−4 cos^4 20°+2 cos^2 20°] =4(1−cos^2 20°)=4 sin^2 20° ⇒DE=2 sin 20° ((CE)/(sin 10°))=((AE)/(sin 20°)) ⇒CE=((sin 10°)/(sin 20°))×AE=((sin 10°)/(sin 20°))×2 cos 10°=((sin 20°)/(sin 20°))=1 ((CE)/(sin ∠CDE))=((DE)/(sin 20°)) ⇒sin ∠CDE=((CE)/(DE))×sin 20°=((1×sin 20°)/(2 sin 20°))=(1/2) ⇒∠CDE=30° ⇒x=∠CDE−10°=30°−10°=20° For this result one doesn′t need to use a calculator.](https://www.tinkutara.com/question/Q43831.png)
$${let}\:{AB}=\mathrm{1} \\ $$$$ \\ $$$$\frac{{AE}}{\mathrm{sin}\:\mathrm{80}°}=\frac{{AB}}{\mathrm{sin}\:\mathrm{30}°} \\ $$$$\Rightarrow{AE}=\frac{\mathrm{sin}\:\mathrm{80}°}{\mathrm{sin}\:\mathrm{30}°}×{AB}=\mathrm{2}\:\mathrm{sin}\:\mathrm{80}°=\mathrm{2}\:\mathrm{cos}\:\mathrm{10}° \\ $$$$ \\ $$$$\frac{{BD}}{\mathrm{sin}\:\mathrm{80}°}=\frac{{AB}}{\mathrm{sin}\:\mathrm{40}°} \\ $$$$\Rightarrow{BD}=\frac{\mathrm{sin}\:\mathrm{80}°}{\mathrm{sin}\:\mathrm{40}°}×{AB}=\mathrm{2}\:\mathrm{cos}\:\mathrm{40}° \\ $$$$ \\ $$$$\frac{{BE}}{\mathrm{sin}\:\mathrm{70}°}=\frac{{AB}}{\mathrm{sin}\:\mathrm{30}°} \\ $$$$\Rightarrow{BE}=\frac{\mathrm{sin}\:\mathrm{70}°}{\mathrm{sin}\:\mathrm{30}°}×{AB}=\mathrm{2}\:\mathrm{sin}\:\mathrm{70}°=\mathrm{2}\:\mathrm{cos}\:\mathrm{20}° \\ $$$$ \\ $$$${DE}^{\mathrm{2}} ={BD}^{\mathrm{2}} +{BE}^{\mathrm{2}} −\mathrm{2}×{BD}×{BE}×\mathrm{cos}\:\mathrm{20}° \\ $$$$=\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\mathrm{40}°+\:\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\mathrm{20}°−\mathrm{8}\:\mathrm{cos}\:\mathrm{40}°\:\mathrm{cos}\:\mathrm{20}°\:\mathrm{cos}\:\mathrm{20}^{\mathrm{2}} \\ $$$$=\mathrm{4}\:\left(\mathrm{cos}^{\mathrm{2}} \:\mathrm{40}°+\:\mathrm{cos}^{\mathrm{2}} \:\mathrm{20}°−\mathrm{2}\:\mathrm{cos}\:\mathrm{40}°\:\mathrm{cos}^{\mathrm{2}} \:\mathrm{20}°\right) \\ $$$$=\mathrm{4}\:\left[\left(\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:\mathrm{20}°−\mathrm{1}\right)^{\mathrm{2}} +\:\mathrm{cos}^{\mathrm{2}} \:\mathrm{20}°−\mathrm{2}\:\left(\mathrm{2}×\mathrm{cos}^{\mathrm{2}} \:\mathrm{20}°−\mathrm{1}\right)\:\mathrm{cos}^{\mathrm{2}} \:\mathrm{20}°\right] \\ $$$$=\mathrm{4}\:\left[\mathrm{4}\:\mathrm{cos}^{\mathrm{4}} \:\mathrm{20}°−\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\mathrm{20}°+\mathrm{1}+\:\mathrm{cos}^{\mathrm{2}} \:\mathrm{20}°−\mathrm{4}\:\mathrm{cos}^{\mathrm{4}} \:\mathrm{20}°+\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:\mathrm{20}°\right] \\ $$$$=\mathrm{4}\left(\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:\mathrm{20}°\right)=\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:\mathrm{20}° \\ $$$$\Rightarrow{DE}=\mathrm{2}\:\mathrm{sin}\:\mathrm{20}° \\ $$$$ \\ $$$$\frac{{CE}}{\mathrm{sin}\:\mathrm{10}°}=\frac{{AE}}{\mathrm{sin}\:\mathrm{20}°} \\ $$$$\Rightarrow{CE}=\frac{\mathrm{sin}\:\mathrm{10}°}{\mathrm{sin}\:\mathrm{20}°}×{AE}=\frac{\mathrm{sin}\:\mathrm{10}°}{\mathrm{sin}\:\mathrm{20}°}×\mathrm{2}\:\mathrm{cos}\:\mathrm{10}°=\frac{\mathrm{sin}\:\mathrm{20}°}{\mathrm{sin}\:\mathrm{20}°}=\mathrm{1} \\ $$$$ \\ $$$$\frac{{CE}}{\mathrm{sin}\:\angle{CDE}}=\frac{{DE}}{\mathrm{sin}\:\mathrm{20}°} \\ $$$$\Rightarrow\mathrm{sin}\:\angle{CDE}=\frac{{CE}}{{DE}}×\mathrm{sin}\:\mathrm{20}°=\frac{\mathrm{1}×\mathrm{sin}\:\mathrm{20}°}{\mathrm{2}\:\mathrm{sin}\:\mathrm{20}°}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\angle{CDE}=\mathrm{30}° \\ $$$$ \\ $$$$\Rightarrow{x}=\angle{CDE}−\mathrm{10}°=\mathrm{30}°−\mathrm{10}°=\mathrm{20}° \\ $$$$ \\ $$$${For}\:{this}\:{result}\:{one}\:{doesn}'{t}\:{need}\:{to}\:{use} \\ $$$${a}\:{calculator}. \\ $$
Commented by peter frank last updated on 22/Apr/20

$${thank}\:{you} \\ $$
Commented by peter frank last updated on 22/Apr/20

$${thank}\:{you} \\ $$
