Question-43731

Question Number 43731 by Meritguide1234 last updated on 14/Sep/18

Answered by MJS last updated on 14/Sep/18

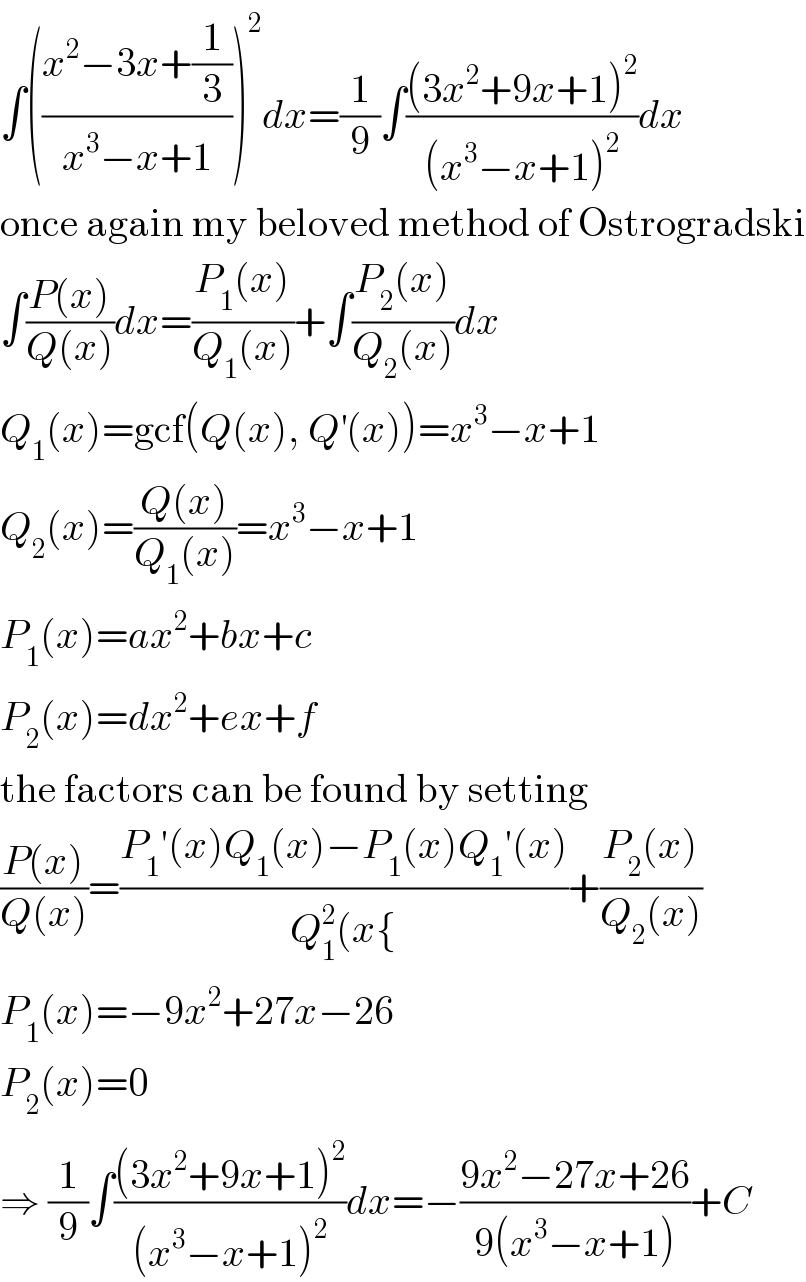
∫(((x^2 −3x+(1/3))/(x^3 −x+1)))^2 dx=(1/9)∫(((3x^2 +9x+1)^2 )/((x^3 −x+1)^2 ))dx once again my beloved method of Ostrogradski ∫((P(x))/(Q(x)))dx=((P_1 (x))/(Q_1 (x)))+∫((P_2 (x))/(Q_2 (x)))dx Q_1 (x)=gcf(Q(x), Q^′ (x))=x^3 −x+1 Q_2 (x)=((Q(x))/(Q_1 (x)))=x^3 −x+1 P_1 (x)=ax^2 +bx+c P_2 (x)=dx^2 +ex+f the factors can be found by setting ((P(x))/(Q(x)))=((P_1 ′(x)Q_1 (x)−P_1 (x)Q_1 ′(x))/(Q_1 ^2 (x{))+((P_2 (x))/(Q_2 (x))) P_1 (x)=−9x^2 +27x−26 P_2 (x)=0 ⇒ (1/9)∫(((3x^2 +9x+1)^2 )/((x^3 −x+1)^2 ))dx=−((9x^2 −27x+26)/(9(x^3 −x+1)))+C

$$\int\left(\frac{{x}^{\mathrm{2}} −\mathrm{3}{x}+\frac{\mathrm{1}}{\mathrm{3}}}{{x}^{\mathrm{3}} −{x}+\mathrm{1}}\right)^{\mathrm{2}} {dx}=\frac{\mathrm{1}}{\mathrm{9}}\int\frac{\left(\mathrm{3}{x}^{\mathrm{2}} +\mathrm{9}{x}+\mathrm{1}\right)^{\mathrm{2}} }{\left({x}^{\mathrm{3}} −{x}+\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$$$\mathrm{once}\:\mathrm{again}\:\mathrm{my}\:\mathrm{beloved}\:\mathrm{method}\:\mathrm{of}\:\mathrm{Ostrogradski} \\ $$$$\int\frac{{P}\left({x}\right)}{{Q}\left({x}\right)}{dx}=\frac{{P}_{\mathrm{1}} \left({x}\right)}{{Q}_{\mathrm{1}} \left({x}\right)}+\int\frac{{P}_{\mathrm{2}} \left({x}\right)}{{Q}_{\mathrm{2}} \left({x}\right)}{dx} \\ $$$${Q}_{\mathrm{1}} \left({x}\right)=\mathrm{gcf}\left({Q}\left({x}\right),\:{Q}^{'} \left({x}\right)\right)={x}^{\mathrm{3}} −{x}+\mathrm{1} \\ $$$${Q}_{\mathrm{2}} \left({x}\right)=\frac{{Q}\left({x}\right)}{{Q}_{\mathrm{1}} \left({x}\right)}={x}^{\mathrm{3}} −{x}+\mathrm{1} \\ $$$${P}_{\mathrm{1}} \left({x}\right)={ax}^{\mathrm{2}} +{bx}+{c} \\ $$$${P}_{\mathrm{2}} \left({x}\right)={dx}^{\mathrm{2}} +{ex}+{f} \\ $$$$\mathrm{the}\:\mathrm{factors}\:\mathrm{can}\:\mathrm{be}\:\mathrm{found}\:\mathrm{by}\:\mathrm{setting} \\ $$$$\frac{{P}\left({x}\right)}{{Q}\left({x}\right)}=\frac{{P}_{\mathrm{1}} '\left({x}\right){Q}_{\mathrm{1}} \left({x}\right)−{P}_{\mathrm{1}} \left({x}\right){Q}_{\mathrm{1}} '\left({x}\right)}{{Q}_{\mathrm{1}} ^{\mathrm{2}} \left({x}\left\{\right.\right.}+\frac{{P}_{\mathrm{2}} \left({x}\right)}{{Q}_{\mathrm{2}} \left({x}\right)} \\ $$$${P}_{\mathrm{1}} \left({x}\right)=−\mathrm{9}{x}^{\mathrm{2}} +\mathrm{27}{x}−\mathrm{26} \\ $$$${P}_{\mathrm{2}} \left({x}\right)=\mathrm{0} \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{\mathrm{9}}\int\frac{\left(\mathrm{3}{x}^{\mathrm{2}} +\mathrm{9}{x}+\mathrm{1}\right)^{\mathrm{2}} }{\left({x}^{\mathrm{3}} −{x}+\mathrm{1}\right)^{\mathrm{2}} }{dx}=−\frac{\mathrm{9}{x}^{\mathrm{2}} −\mathrm{27}{x}+\mathrm{26}}{\mathrm{9}\left({x}^{\mathrm{3}} −{x}+\mathrm{1}\right)}+{C} \\ $$

Commented by Meritguide1234 last updated on 15/Sep/18

Facebook Tweet Pin

Leave a Reply Cancel reply