Menu Close

Question-43759

Tinku Tara 0 Comments
Pin




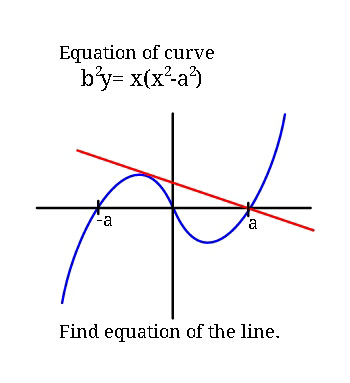
Question Number 43759 by ajfour last updated on 15/Sep/18
Answered by MrW3 last updated on 15/Sep/18
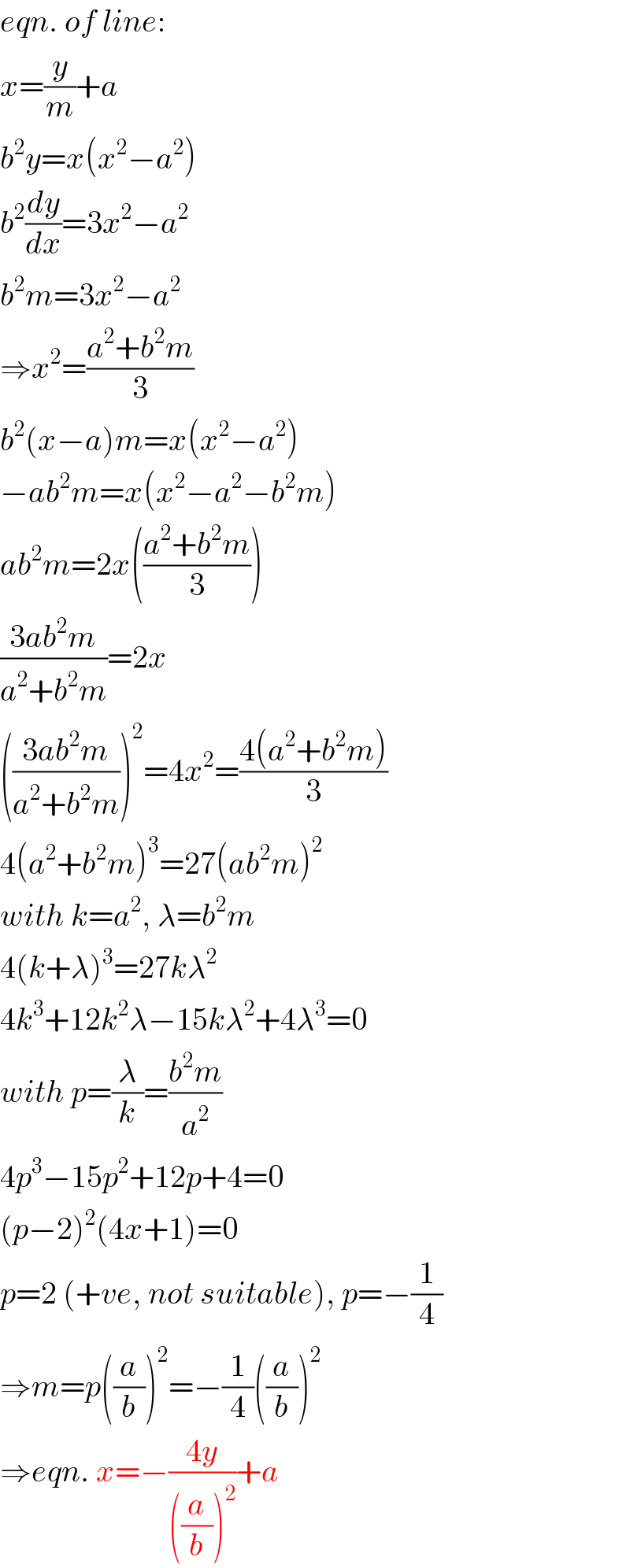
eqn. of line: x=(y/m)+a b^2 y=x(x^2 −a^2 ) b^2 (dy/dx)=3x^2 −a^2 b^2 m=3x^2 −a^2 ⇒x^2 =((a^2 +b^2 m)/3) b^2 (x−a)m=x(x^2 −a^2 ) −ab^2 m=x(x^2 −a^2 −b^2 m) ab^2 m=2x(((a^2 +b^2 m)/3)) ((3ab^2 m)/(a^2 +b^2 m))=2x (((3ab^2 m)/(a^2 +b^2 m)))^2 =4x^2 =((4(a^2 +b^2 m))/3) 4(a^2 +b^2 m)^3 =27(ab^2 m)^2 with k=a^2 , λ=b^2 m 4(k+λ)^3 =27kλ^2 4k^3 +12k^2 λ−15kλ^2 +4λ^3 =0 with p=(λ/k)=((b^2 m)/a^2 ) 4p^3 −15p^2 +12p+4=0 (p−2)^2 (4x+1)=0 p=2 (+ve, not suitable), p=−(1/4) ⇒m=p((a/b))^2 =−(1/4)((a/b))^2 ⇒eqn. x=−((4y)/(((a/b))^2 ))+a
$${eqn}.\:{of}\:{line}: \\ $$$${x}=\frac{{y}}{{m}}+{a} \\ $$$${b}^{\mathrm{2}} {y}={x}\left({x}^{\mathrm{2}} −{a}^{\mathrm{2}} \right) \\ $$$${b}^{\mathrm{2}} \frac{{dy}}{{dx}}=\mathrm{3}{x}^{\mathrm{2}} −{a}^{\mathrm{2}} \\ $$$${b}^{\mathrm{2}} {m}=\mathrm{3}{x}^{\mathrm{2}} −{a}^{\mathrm{2}} \\ $$$$\Rightarrow{x}^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} {m}}{\mathrm{3}} \\ $$$${b}^{\mathrm{2}} \left({x}−{a}\right){m}={x}\left({x}^{\mathrm{2}} −{a}^{\mathrm{2}} \right) \\ $$$$−{ab}^{\mathrm{2}} {m}={x}\left({x}^{\mathrm{2}} −{a}^{\mathrm{2}} −{b}^{\mathrm{2}} {m}\right) \\ $$$${ab}^{\mathrm{2}} {m}=\mathrm{2}{x}\left(\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} {m}}{\mathrm{3}}\right) \\ $$$$\frac{\mathrm{3}{ab}^{\mathrm{2}} {m}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} {m}}=\mathrm{2}{x} \\ $$$$\left(\frac{\mathrm{3}{ab}^{\mathrm{2}} {m}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} {m}}\right)^{\mathrm{2}} =\mathrm{4}{x}^{\mathrm{2}} =\frac{\mathrm{4}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} {m}\right)}{\mathrm{3}} \\ $$$$\mathrm{4}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} {m}\right)^{\mathrm{3}} =\mathrm{27}\left({ab}^{\mathrm{2}} {m}\right)^{\mathrm{2}} \\ $$$${with}\:{k}={a}^{\mathrm{2}} ,\:\lambda={b}^{\mathrm{2}} {m} \\ $$$$\mathrm{4}\left({k}+\lambda\right)^{\mathrm{3}} =\mathrm{27}{k}\lambda^{\mathrm{2}} \\ $$$$\mathrm{4}{k}^{\mathrm{3}} +\mathrm{12}{k}^{\mathrm{2}} \lambda−\mathrm{15}{k}\lambda^{\mathrm{2}} +\mathrm{4}\lambda^{\mathrm{3}} =\mathrm{0} \\ $$$${with}\:{p}=\frac{\lambda}{{k}}=\frac{{b}^{\mathrm{2}} {m}}{{a}^{\mathrm{2}} } \\ $$$$\mathrm{4}{p}^{\mathrm{3}} −\mathrm{15}{p}^{\mathrm{2}} +\mathrm{12}{p}+\mathrm{4}=\mathrm{0} \\ $$$$\left({p}−\mathrm{2}\right)^{\mathrm{2}} \left(\mathrm{4}{x}+\mathrm{1}\right)=\mathrm{0} \\ $$$${p}=\mathrm{2}\:\left(+{ve},\:{not}\:{suitable}\right),\:{p}=−\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow{m}={p}\left(\frac{{a}}{{b}}\right)^{\mathrm{2}} =−\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{{a}}{{b}}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{eqn}.\:{x}=−\frac{\mathrm{4}{y}}{\left(\frac{{a}}{{b}}\right)^{\mathrm{2}} }+{a} \\ $$
Commented by MrW3 last updated on 15/Sep/18
Commented by ajfour last updated on 15/Sep/18
Thanks sir, see my solution!
$${Thanks}\:{sir},\:{see}\:{my}\:{solution}! \\ $$
Answered by ajfour last updated on 15/Sep/18
let eq. of line be: y=m(x−a) eq. of curve: b^2 y=x(x^2 −a^2 ) solving simultaneously (y/(x−a)) = m =((x(x+a))/b^2 ) ⇒ x^2 +ax−b^2 m=0 for unique x value 4b^2 m = −a^2 or m=−(a^2 /(4b^2 )) eq. of line is then y=−(a^2 /(4b^2 ))(x−a) or 4b^2 y = a^2 (a−x) .
$${let}\:{eq}.\:{of}\:{line}\:{be}:\:\:\:\boldsymbol{{y}}=\boldsymbol{{m}}\left(\boldsymbol{{x}}−\boldsymbol{{a}}\right) \\ $$$${eq}.\:{of}\:{curve}:\:\:\:\:\boldsymbol{{b}}^{\mathrm{2}} \boldsymbol{{y}}=\boldsymbol{{x}}\left(\boldsymbol{{x}}^{\mathrm{2}} −\boldsymbol{{a}}^{\mathrm{2}} \right) \\ $$$$\:{solving}\:{simultaneously} \\ $$$$\:\:\frac{{y}}{{x}−{a}}\:=\:{m}\:=\frac{{x}\left({x}+{a}\right)}{{b}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\:\:\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{ax}}−\boldsymbol{{b}}^{\mathrm{2}} \boldsymbol{{m}}=\mathrm{0} \\ $$$${for}\:{unique}\:\:\boldsymbol{{x}}\:{value} \\ $$$$\:\:\:\:\:\:\mathrm{4}\boldsymbol{{b}}^{\mathrm{2}} \boldsymbol{{m}}\:=\:−\boldsymbol{{a}}^{\mathrm{2}} \\ $$$${or}\:\:\:\:\:\boldsymbol{{m}}=−\frac{\boldsymbol{{a}}^{\mathrm{2}} }{\mathrm{4}\boldsymbol{{b}}^{\mathrm{2}} } \\ $$$$\boldsymbol{{eq}}.\:\boldsymbol{{of}}\:\boldsymbol{{line}}\:{is}\:{then} \\ $$$$\:\:\:\:\:\:\:\:\boldsymbol{{y}}=−\frac{\boldsymbol{{a}}^{\mathrm{2}} }{\mathrm{4}\boldsymbol{{b}}^{\mathrm{2}} }\left(\boldsymbol{{x}}−\boldsymbol{{a}}\right) \\ $$$${or}\:\:\:\:\mathrm{4}\boldsymbol{{b}}^{\mathrm{2}} \boldsymbol{{y}}\:=\:\boldsymbol{{a}}^{\mathrm{2}} \left(\boldsymbol{{a}}−\boldsymbol{{x}}\right)\:. \\ $$
Commented by MrW3 last updated on 15/Sep/18
super solution!
$${super}\:{solution}! \\ $$
Commented by ajfour last updated on 15/Sep/18
thanks for the adjective Sir!
$${thanks}\:{for}\:{the}\:{adjective}\:{Sir}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *