Menu Close

Question-43825

Tinku Tara 0 Comments
Pin




Question Number 43825 by Necxx last updated on 15/Sep/18
Answered by tanmay.chaudhury50@gmail.com last updated on 17/Sep/18
Commented by tanmay.chaudhury50@gmail.com last updated on 17/Sep/18
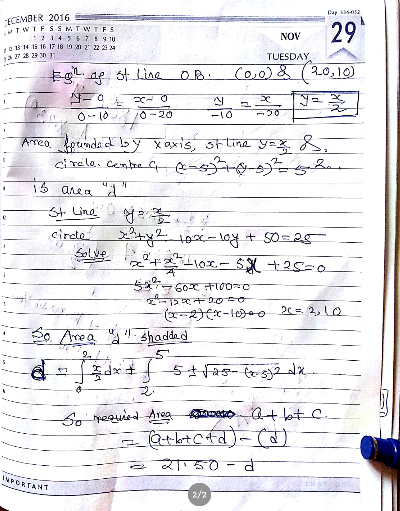
Commented by tanmay.chaudhury50@gmail.com last updated on 17/Sep/18
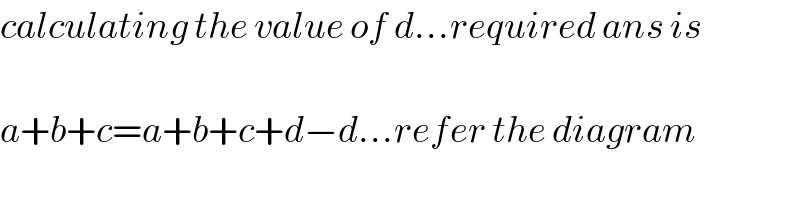
calculating the value of d...required ans is a+b+c=a+b+c+d−d...refer the diagram
$${calculating}\:{the}\:{value}\:{of}\:{d}…{required}\:{ans}\:{is} \\ $$$$ \\ $$$${a}+{b}+{c}={a}+{b}+{c}+{d}−{d}…{refer}\:{the}\:{diagram} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 17/Sep/18
d=∫_0 ^2 (x/2)dx+∫_2 ^5 5±(√(25−(x−5)^2 )) dx =∫_0 ^2 (x/2)dx+∫_2 ^5 5±(√(25−(x−5)^2 )) dx =∣(x^2 /4)∣_0 ^2 +5∣x∣_2 ^5 ±I =1+15±I =16±I ∫_2 ^5 (√(25−(x−5)^2 )) dx ∣((x−5)/2)(√(25−(x−5)^2 )) +((25)/2)sin^(−1) (((x−5)/5))∣_2 ^5 upper limit gives value 0 putting lower limit {((−3)/2)×4+((25)/2)sin^(−1) (−(3/5))} =−6+12.5sin^(−1) (((−3)/5)) =−6+12.5(−((37×Π)/5)) =−6−2.57Π I=0−{−6−2.57Π} I=6+2.57Π 16±(6+2.57Π) =22+2.57Π and 10−2.57Π value of d 22+2.57Π ←not feasible so d=10−2.57Π so required answer is a+b+c+d−d =21.50−(10−2.57𝚷) =11.50+2.57Π pls check...
$${d}=\int_{\mathrm{0}} ^{\mathrm{2}} \frac{{x}}{\mathrm{2}}{dx}+\int_{\mathrm{2}} ^{\mathrm{5}} \mathrm{5}\pm\sqrt{\mathrm{25}−\left({x}−\mathrm{5}\right)^{\mathrm{2}} \:}\:{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{2}} \frac{{x}}{\mathrm{2}}{dx}+\int_{\mathrm{2}} ^{\mathrm{5}} \mathrm{5}\pm\sqrt{\mathrm{25}−\left({x}−\mathrm{5}\right)^{\mathrm{2}} }\:{dx} \\ $$$$=\mid\frac{{x}^{\mathrm{2}} }{\mathrm{4}}\mid_{\mathrm{0}} ^{\mathrm{2}} +\mathrm{5}\mid{x}\mid_{\mathrm{2}} ^{\mathrm{5}} \:\pm{I} \\ $$$$=\mathrm{1}+\mathrm{15}\pm{I} \\ $$$$=\mathrm{16}\pm{I} \\ $$$$\int_{\mathrm{2}} ^{\mathrm{5}} \sqrt{\mathrm{25}−\left({x}−\mathrm{5}\right)^{\mathrm{2}} }\:{dx} \\ $$$$\mid\frac{{x}−\mathrm{5}}{\mathrm{2}}\sqrt{\mathrm{25}−\left({x}−\mathrm{5}\right)^{\mathrm{2}} }\:\:+\frac{\mathrm{25}}{\mathrm{2}}{sin}^{−\mathrm{1}} \left(\frac{{x}−\mathrm{5}}{\mathrm{5}}\right)\mid_{\mathrm{2}} ^{\mathrm{5}} \\ $$$${upper}\:{limit}\:{gives}\:{value}\:\mathrm{0} \\ $$$${putting}\:{lower}\:{limit} \\ $$$$\left\{\frac{−\mathrm{3}}{\mathrm{2}}×\mathrm{4}+\frac{\mathrm{25}}{\mathrm{2}}{sin}^{−\mathrm{1}} \left(−\frac{\mathrm{3}}{\mathrm{5}}\right)\right\} \\ $$$$=−\mathrm{6}+\mathrm{12}.\mathrm{5}{sin}^{−\mathrm{1}} \left(\frac{−\mathrm{3}}{\mathrm{5}}\right) \\ $$$$=−\mathrm{6}+\mathrm{12}.\mathrm{5}\left(−\frac{\mathrm{37}×\Pi}{\mathrm{5}}\right) \\ $$$$=−\mathrm{6}−\mathrm{2}.\mathrm{57}\Pi \\ $$$${I}=\mathrm{0}−\left\{−\mathrm{6}−\mathrm{2}.\mathrm{57}\Pi\right\} \\ $$$${I}=\mathrm{6}+\mathrm{2}.\mathrm{57}\Pi \\ $$$$\mathrm{16}\pm\left(\mathrm{6}+\mathrm{2}.\mathrm{57}\Pi\right) \\ $$$$=\mathrm{22}+\mathrm{2}.\mathrm{57}\Pi\:{and}\:\mathrm{10}−\mathrm{2}.\mathrm{57}\Pi \\ $$$${value}\:{of}\:{d}\:\mathrm{22}+\mathrm{2}.\mathrm{57}\Pi\:\leftarrow{not}\:{feasible} \\ $$$${so}\:{d}=\mathrm{10}−\mathrm{2}.\mathrm{57}\Pi \\ $$$$ \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{required}}\:\boldsymbol{{answer}}\:\boldsymbol{{is}} \\ $$$$\boldsymbol{{a}}+\boldsymbol{{b}}+\boldsymbol{{c}}+\boldsymbol{{d}}−\boldsymbol{{d}} \\ $$$$=\mathrm{21}.\mathrm{50}−\left(\mathrm{10}−\mathrm{2}.\mathrm{57}\boldsymbol{\Pi}\right) \\ $$$$=\mathrm{11}.\mathrm{50}+\mathrm{2}.\mathrm{57}\Pi \\ $$$$\boldsymbol{{pls}}\:\boldsymbol{{check}}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *