Menu Close

Question-43832

Tinku Tara 0 Comments
Pin




Question Number 43832 by physics last updated on 16/Sep/18
Commented by physics last updated on 16/Sep/18
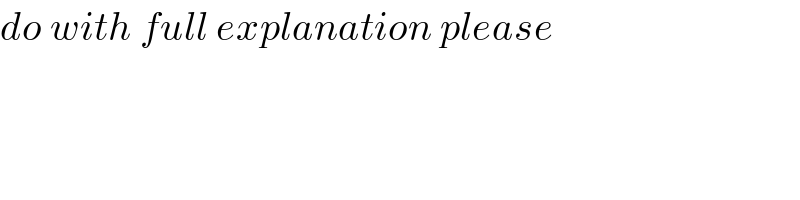
do with full explanation please
$${do}\:{with}\:{full}\:{explanation}\:{please} \\ $$
Commented by maxmathsup by imad last updated on 16/Sep/18
let A =∫ (dx/((x^2 +a^2 )^(3/2) )) changement x=ash(t)give t=argsh((x/a))and A = ∫ ((ach(t) dt)/(a^3 (ch^2 (t))^(3/2) )) =(1/a^2 ) ∫ (dt/(ch^2 (t))) (we suppose a≠0) A = (2/a^2 ) ∫ (dt/(1+ch(2t))) =(2/a^2 ) ∫ (dt/(1+((e^(2t) +e^(−2t) )/2))) =(4/a^2 ) ∫ (dt/(2 +e^(2t) +e^(−2t) )) =_(e^(2t) =u) (4/a^2 ) ∫ (1/(2 +u +u^(−1) )) (du/(2u)) =(2/a^2 ) ∫ (du/(2u +u^2 +1)) =(2/a^2 ) ∫ (du/((u+1)^2 )) =((−2)/(a^2 (u+1))) +c =−(2/(a^2 ( 1+e^(2t) ))) but t=ln((x/a) +(√(1+(x^2 /a^2 )))) ⇒ e^(2t) =((x/a) +(√(1+(x^2 /a^2 ))))^2 ⇒A =((−2)/(a^2 (1+((x/a)+(√(1+(x^2 /a^2 ))))^2 )) +c if a=0 A = ∫ (dx/x^3 ) =∫ x^(−3) dx =(1/(−3+1))x^(−3+1) +c =((−1)/(2x^2 )) +c .
$${let}\:{A}\:=\int\:\:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} \:+{a}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} }\:\:{changement}\:{x}={ash}\left({t}\right){give}\:{t}={argsh}\left(\frac{{x}}{{a}}\right){and} \\ $$$${A}\:=\:\int\:\:\:\frac{{ach}\left({t}\right)\:{dt}}{{a}^{\mathrm{3}} \left({ch}^{\mathrm{2}} \left({t}\right)\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }\:=\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\:\int\:\:\:\:\frac{{dt}}{{ch}^{\mathrm{2}} \left({t}\right)}\:\:\:\:\:\:\:\:\:\left({we}\:{suppose}\:{a}\neq\mathrm{0}\right) \\ $$$${A}\:=\:\frac{\mathrm{2}}{{a}^{\mathrm{2}} }\:\int\:\:\:\:\:\:\frac{{dt}}{\mathrm{1}+{ch}\left(\mathrm{2}{t}\right)}\:=\frac{\mathrm{2}}{{a}^{\mathrm{2}} }\:\int\:\:\:\frac{{dt}}{\mathrm{1}+\frac{{e}^{\mathrm{2}{t}} \:+{e}^{−\mathrm{2}{t}} }{\mathrm{2}}}\:=\frac{\mathrm{4}}{{a}^{\mathrm{2}} }\:\int\:\:\:\:\frac{{dt}}{\mathrm{2}\:+{e}^{\mathrm{2}{t}} \:+{e}^{−\mathrm{2}{t}} } \\ $$$$=_{{e}^{\mathrm{2}{t}} ={u}} \:\:\:\:\:\frac{\mathrm{4}}{{a}^{\mathrm{2}} }\:\int\:\:\:\frac{\mathrm{1}}{\mathrm{2}\:+{u}\:+{u}^{−\mathrm{1}} }\:\frac{{du}}{\mathrm{2}{u}}\:=\frac{\mathrm{2}}{{a}^{\mathrm{2}} }\:\int\:\:\:\:\frac{{du}}{\mathrm{2}{u}\:+{u}^{\mathrm{2}} \:+\mathrm{1}}\:=\frac{\mathrm{2}}{{a}^{\mathrm{2}} }\:\int\:\:\frac{{du}}{\left({u}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{−\mathrm{2}}{{a}^{\mathrm{2}} \left({u}+\mathrm{1}\right)}\:+{c}\:=−\frac{\mathrm{2}}{{a}^{\mathrm{2}} \left(\:\mathrm{1}+{e}^{\mathrm{2}{t}} \right)}\:{but}\:{t}={ln}\left(\frac{{x}}{{a}}\:+\sqrt{\mathrm{1}+\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }}\right)\:\Rightarrow \\ $$$${e}^{\mathrm{2}{t}} \:=\left(\frac{{x}}{{a}}\:+\sqrt{\mathrm{1}+\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }}\right)^{\mathrm{2}} \:\Rightarrow{A}\:=\frac{−\mathrm{2}}{{a}^{\mathrm{2}} \left(\mathrm{1}+\left(\frac{{x}}{{a}}+\sqrt{\mathrm{1}+\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }}\right)^{\mathrm{2}} \right.}\:+{c}\: \\ $$$${if}\:{a}=\mathrm{0}\:{A}\:=\:\int\:\:\frac{{dx}}{{x}^{\mathrm{3}} }\:=\int\:{x}^{−\mathrm{3}} {dx}\:=\frac{\mathrm{1}}{−\mathrm{3}+\mathrm{1}}{x}^{−\mathrm{3}+\mathrm{1}} \:+{c}\:=\frac{−\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }\:+{c}\:. \\ $$
Answered by MJS last updated on 16/Sep/18
∫(dx/((x^2 +a^2 )^(3/2) ))= [x=atan t → t=arctan (x/a) → dx=asec^2 t dt] =∫((asec^2 t)/((a^2 +a^2 tan^2 t)^(3/2) ))dt=∫((asec^2 t)/(a^3 (1+tan^2 t)))dt= [1+tan^2 t =1+((sin^2 t)/(cos^2 t))=((cos^2 t +sin^2 t)/(cos^2 t))=(1/(cos^2 t))=sec^2 t] =(1/a^2 )∫((sec^2 t)/((sec^2 t)^(3/2) ))dt=(1/a^2 )∫(dt/(sec t))=(1/a^2 )∫cos t dt= =(1/a^2 )sin t =(1/a^2 )sin arctan (x/a)= [sin arctan t =(t/( (√(t^2 +1))))] =(x/(a^3 (√((x^2 /a^2 )+1))))=(x/(a^2 (√(x^2 +a^2 ))))+C
$$\int\frac{{dx}}{\left({x}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} }= \\ $$$$\:\:\:\:\:\left[{x}={a}\mathrm{tan}\:{t}\:\rightarrow\:{t}=\mathrm{arctan}\:\frac{{x}}{{a}}\:\rightarrow\:{dx}={a}\mathrm{sec}^{\mathrm{2}} \:{t}\:{dt}\right] \\ $$$$=\int\frac{{a}\mathrm{sec}^{\mathrm{2}} \:{t}}{\left({a}^{\mathrm{2}} +{a}^{\mathrm{2}} \mathrm{tan}^{\mathrm{2}} \:{t}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{dt}=\int\frac{{a}\mathrm{sec}^{\mathrm{2}} \:{t}}{{a}^{\mathrm{3}} \left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:{t}\right)}{dt}= \\ $$$$\:\:\:\:\:\left[\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:{t}\:=\mathrm{1}+\frac{\mathrm{sin}^{\mathrm{2}} \:{t}}{\mathrm{cos}^{\mathrm{2}} \:{t}}=\frac{\mathrm{cos}^{\mathrm{2}} \:{t}\:+\mathrm{sin}^{\mathrm{2}} \:{t}}{\mathrm{c}{o}\mathrm{s}^{\mathrm{2}} \:{t}}=\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \:{t}}=\mathrm{sec}^{\mathrm{2}} \:{t}\right] \\ $$$$=\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\int\frac{\mathrm{sec}^{\mathrm{2}} \:{t}}{\left(\mathrm{sec}^{\mathrm{2}} \:{t}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{dt}=\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\int\frac{{dt}}{\mathrm{sec}\:{t}}=\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\int\mathrm{cos}\:{t}\:{dt}= \\ $$$$=\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\mathrm{sin}\:{t}\:=\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\mathrm{sin}\:\mathrm{arctan}\:\frac{{x}}{{a}}= \\ $$$$\:\:\:\:\:\left[\mathrm{sin}\:\mathrm{arctan}\:{t}\:=\frac{{t}}{\:\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}}\right] \\ $$$$=\frac{{x}}{{a}^{\mathrm{3}} \sqrt{\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\mathrm{1}}}=\frac{{x}}{{a}^{\mathrm{2}} \sqrt{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }}+{C} \\ $$
Commented by physics last updated on 19/Sep/18
thank you sir
$${thank}\:{you}\:{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *