Question Number 43992 by ajfour last updated on 19/Sep/18

Commented by ajfour last updated on 19/Sep/18

$${If}\:{square}\:{has}\:{as}\:{much}\:{area}\: \\ $$$${outside}\:{circle}\:{as}\:{circle}\:{has} \\ $$$${outside}\:{square},\:{relate}\:\boldsymbol{{a}},\:{and}\:\boldsymbol{{R}}. \\ $$
Answered by MrW3 last updated on 19/Sep/18

$$\pi{R}^{\mathrm{2}} ={a}^{\mathrm{2}} \\ $$$$\Rightarrow\frac{{a}}{{R}}=\sqrt{\pi} \\ $$
Commented by math1967 last updated on 20/Sep/18
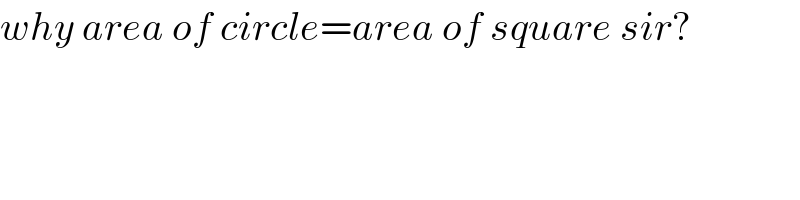
$${why}\:{area}\:{of}\:{circle}={area}\:{of}\:{square}\:{sir}? \\ $$
Commented by MrW3 last updated on 20/Sep/18

Commented by MrW3 last updated on 20/Sep/18
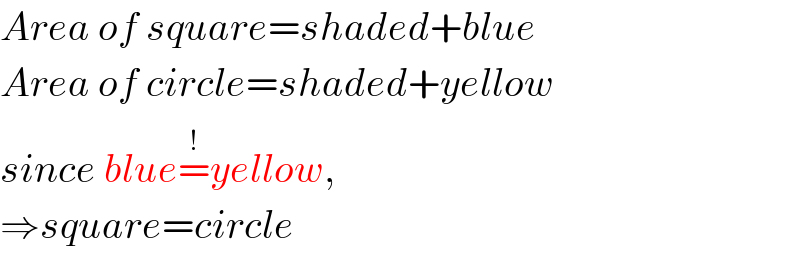
$${Area}\:{of}\:{square}={shaded}+{blue} \\ $$$${Area}\:{of}\:{circle}={shaded}+{yellow} \\ $$$${since}\:{blue}\overset{!} {=}{yellow}, \\ $$$$\Rightarrow{square}={circle} \\ $$
Commented by ajfour last updated on 20/Sep/18

$${common}\:{area}+{circular}\:{segment} \\ $$$${areas}=\:{common}\:{area}+{corner} \\ $$$${segment}\:{areas} \\ $$$$\Rightarrow\:\:\:\pi{R}^{\mathrm{2}} \:=\:{a}^{\mathrm{2}} \:\:\:\:\left({obviously}\right). \\ $$
Commented by math1967 last updated on 20/Sep/18
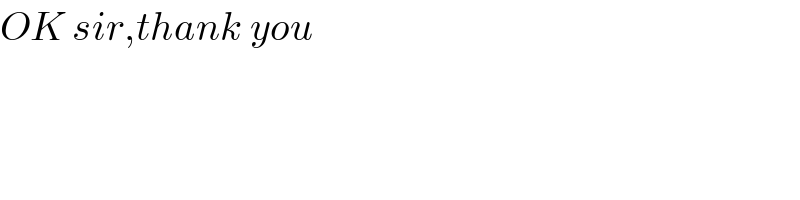
$${OK}\:{sir},{thank}\:{you} \\ $$
