Question Number 44062 by peter frank last updated on 20/Sep/18
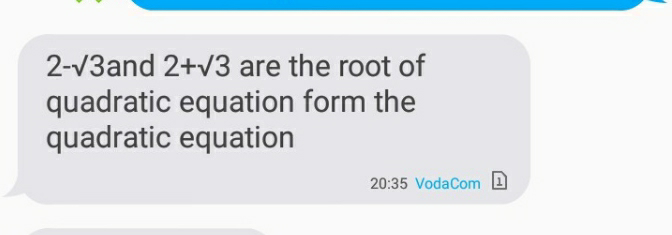
Answered by MJS last updated on 21/Sep/18
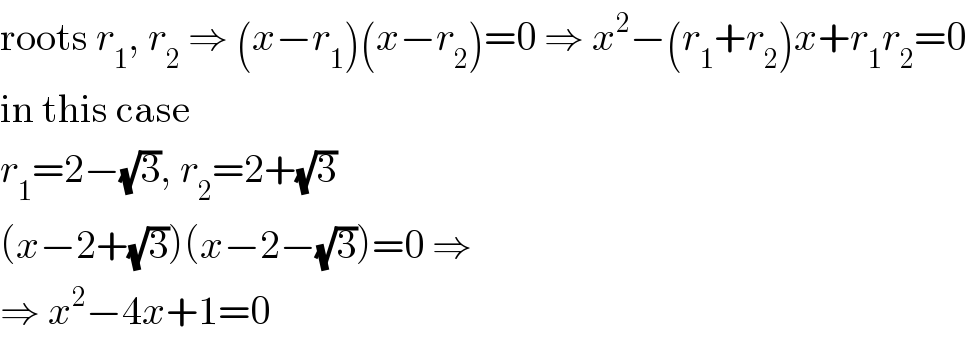
$$\mathrm{roots}\:{r}_{\mathrm{1}} ,\:{r}_{\mathrm{2}} \:\Rightarrow\:\left({x}−{r}_{\mathrm{1}} \right)\left({x}−{r}_{\mathrm{2}} \right)=\mathrm{0}\:\Rightarrow\:{x}^{\mathrm{2}} −\left({r}_{\mathrm{1}} +{r}_{\mathrm{2}} \right){x}+{r}_{\mathrm{1}} {r}_{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{in}\:\mathrm{this}\:\mathrm{case} \\ $$$${r}_{\mathrm{1}} =\mathrm{2}−\sqrt{\mathrm{3}},\:{r}_{\mathrm{2}} =\mathrm{2}+\sqrt{\mathrm{3}} \\ $$$$\left({x}−\mathrm{2}+\sqrt{\mathrm{3}}\right)\left({x}−\mathrm{2}−\sqrt{\mathrm{3}}\right)=\mathrm{0}\:\Rightarrow \\ $$$$\Rightarrow\:{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{1}=\mathrm{0} \\ $$
Commented by $@ty@m last updated on 21/Sep/18
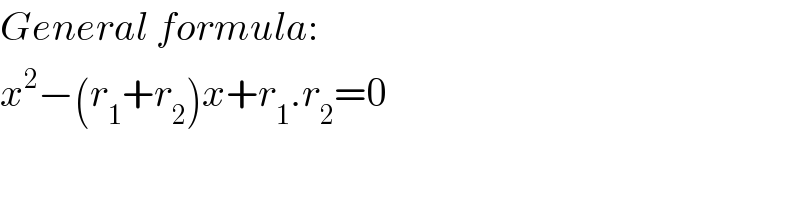
$${General}\:{formula}: \\ $$$${x}^{\mathrm{2}} −\left({r}_{\mathrm{1}} +{r}_{\mathrm{2}} \right){x}+{r}_{\mathrm{1}} .{r}_{\mathrm{2}} =\mathrm{0} \\ $$
