Question Number 44095 by peter frank last updated on 21/Sep/18

Answered by tanmay.chaudhury50@gmail.com last updated on 22/Sep/18
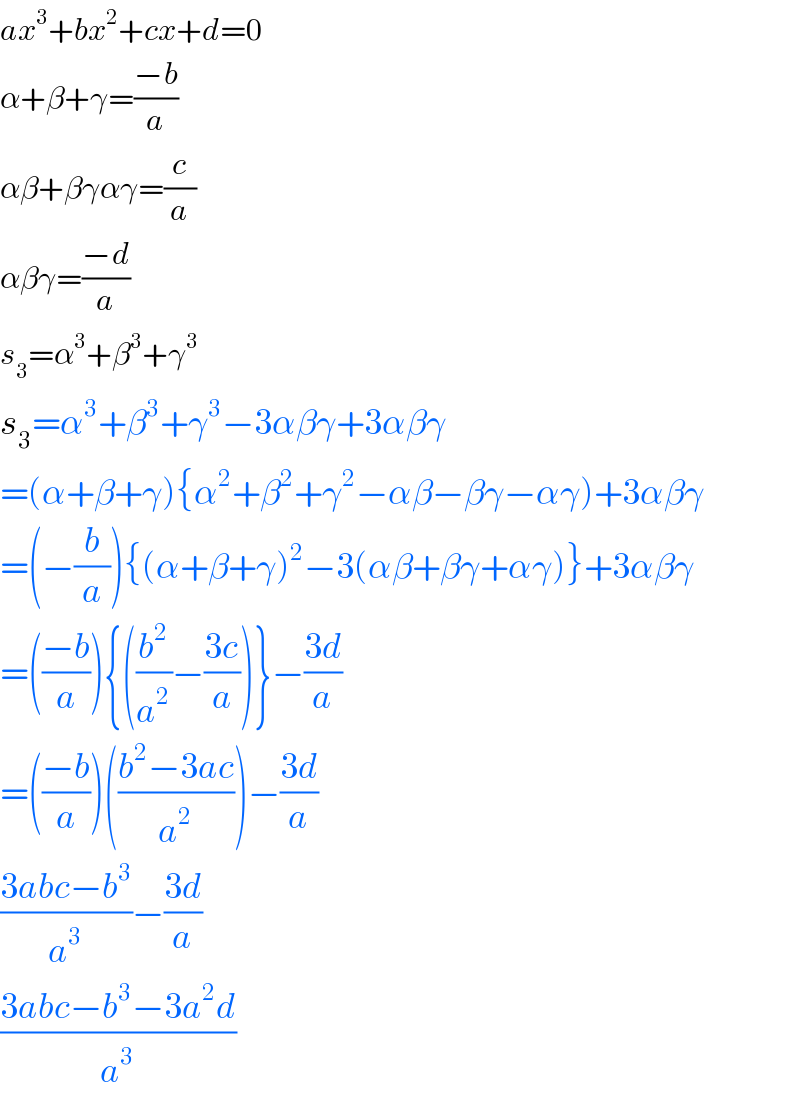
$${ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +{cx}+{d}=\mathrm{0} \\ $$$$\alpha+\beta+\gamma=\frac{−{b}}{{a}} \\ $$$$\alpha\beta+\beta\gamma\alpha\gamma=\frac{{c}}{{a}} \\ $$$$\alpha\beta\gamma=\frac{−{d}}{{a}} \\ $$$${s}_{\mathrm{3}} =\alpha^{\mathrm{3}} +\beta^{\mathrm{3}} +\gamma^{\mathrm{3}} \\ $$$${s}_{\mathrm{3}} =\alpha^{\mathrm{3}} +\beta^{\mathrm{3}} +\gamma^{\mathrm{3}} −\mathrm{3}\alpha\beta\gamma+\mathrm{3}\alpha\beta\gamma \\ $$$$=\left(\alpha+\beta+\gamma\right)\left\{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} −\alpha\beta−\beta\gamma−\alpha\gamma\right)+\mathrm{3}\alpha\beta\gamma \\ $$$$=\left(−\frac{{b}}{{a}}\right)\left\{\left(\alpha+\beta+\gamma\right)^{\mathrm{2}} −\mathrm{3}\left(\alpha\beta+\beta\gamma+\alpha\gamma\right)\right\}+\mathrm{3}\alpha\beta\gamma \\ $$$$=\left(\frac{−{b}}{{a}}\right)\left\{\left(\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }−\frac{\mathrm{3}{c}}{{a}}\right)\right\}−\frac{\mathrm{3}{d}}{{a}} \\ $$$$=\left(\frac{−{b}}{{a}}\right)\left(\frac{{b}^{\mathrm{2}} −\mathrm{3}{ac}}{{a}^{\mathrm{2}} }\right)−\frac{\mathrm{3}{d}}{{a}} \\ $$$$\frac{\mathrm{3}{abc}−{b}^{\mathrm{3}} }{{a}^{\mathrm{3}} }−\frac{\mathrm{3}{d}}{{a}} \\ $$$$\frac{\mathrm{3}{abc}−{b}^{\mathrm{3}} −\mathrm{3}{a}^{\mathrm{2}} {d}}{{a}^{\mathrm{3}} } \\ $$
