Question Number 44098 by peter frank last updated on 21/Sep/18
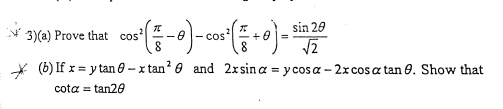
Answered by $@ty@m last updated on 21/Sep/18
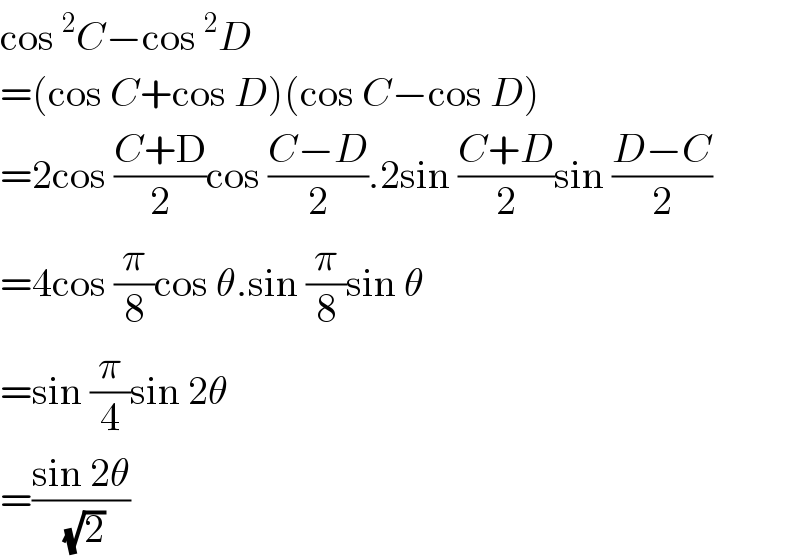
$$\mathrm{cos}\:^{\mathrm{2}} {C}−\mathrm{cos}\:^{\mathrm{2}} {D} \\ $$$$=\left(\mathrm{cos}\:{C}+\mathrm{cos}\:{D}\right)\left(\mathrm{cos}\:{C}−\mathrm{cos}\:{D}\right) \\ $$$$=\mathrm{2cos}\:\frac{{C}+\mathrm{D}}{\mathrm{2}}\mathrm{cos}\:\frac{{C}−{D}}{\mathrm{2}}.\mathrm{2sin}\:\frac{{C}+{D}}{\mathrm{2}}\mathrm{sin}\:\frac{{D}−{C}}{\mathrm{2}} \\ $$$$=\mathrm{4cos}\:\frac{\pi}{\mathrm{8}}\mathrm{cos}\:\theta.\mathrm{sin}\:\frac{\pi}{\mathrm{8}}\mathrm{sin}\:\theta \\ $$$$=\mathrm{sin}\:\frac{\pi}{\mathrm{4}}\mathrm{sin}\:\mathrm{2}\theta \\ $$$$=\frac{\mathrm{sin}\:\mathrm{2}\theta}{\:\sqrt{\mathrm{2}}} \\ $$
Commented by peter frank last updated on 21/Sep/18

$${how}\:{about}\:{b}? \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 21/Sep/18
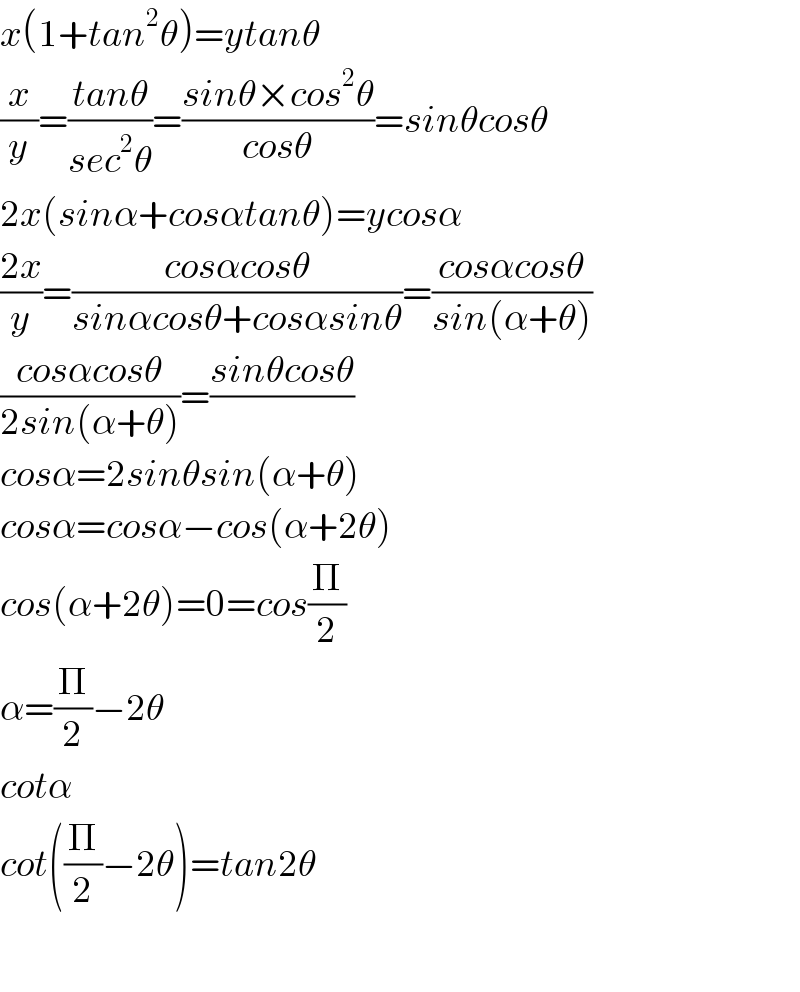
$${x}\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right)={ytan}\theta \\ $$$$\frac{{x}}{{y}}=\frac{{tan}\theta}{{sec}^{\mathrm{2}} \theta}=\frac{{sin}\theta×{cos}^{\mathrm{2}} \theta}{{cos}\theta}={sin}\theta{cos}\theta \\ $$$$\mathrm{2}{x}\left({sin}\alpha+{cos}\alpha{tan}\theta\right)={ycos}\alpha \\ $$$$\frac{\mathrm{2}{x}}{{y}}=\frac{{cos}\alpha{cos}\theta}{{sin}\alpha{cos}\theta+{cos}\alpha{sin}\theta}=\frac{{cos}\alpha{cos}\theta}{{sin}\left(\alpha+\theta\right)} \\ $$$$\frac{{cos}\alpha{cos}\theta}{\mathrm{2}{sin}\left(\alpha+\theta\right)}=\frac{{sin}\theta{cos}\theta}{} \\ $$$${cos}\alpha=\mathrm{2}{sin}\theta{sin}\left(\alpha+\theta\right) \\ $$$${cos}\alpha={cos}\alpha−{cos}\left(\alpha+\mathrm{2}\theta\right) \\ $$$${cos}\left(\alpha+\mathrm{2}\theta\right)=\mathrm{0}={cos}\frac{\Pi}{\mathrm{2}} \\ $$$$\alpha=\frac{\Pi}{\mathrm{2}}−\mathrm{2}\theta \\ $$$${cot}\alpha \\ $$$${cot}\left(\frac{\Pi}{\mathrm{2}}−\mathrm{2}\theta\right)={tan}\mathrm{2}\theta \\ $$$$ \\ $$
Commented by peter frank last updated on 21/Sep/18

$${thank}\:{you} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 21/Sep/18

$${most}\:{welcome}… \\ $$
Answered by $@ty@m last updated on 21/Sep/18

$$\left({b}\right)\:{x}={y}\mathrm{tan}\:\theta−{x}\mathrm{tan}\:^{\mathrm{2}} \theta \\ $$$${x}\left(\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \theta\right)={y}\mathrm{tan}\:\theta \\ $$$$\frac{{x}}{{y}}=\frac{\mathrm{tan}\:\theta}{\mathrm{sec}\:^{\mathrm{2}} \theta}\: \\ $$$$\frac{{x}}{{y}}=\mathrm{sin}\:\theta\mathrm{cos}\:\theta \\ $$$$\frac{\mathrm{2}{x}}{{y}}=\mathrm{sin}\:\mathrm{2}\theta\:….\left(\mathrm{1}\right) \\ $$$$\mathrm{2}{x}\mathrm{sin}\:\alpha={y}\mathrm{cos}\:\alpha−\mathrm{2}{x}\mathrm{cos}\:\alpha\mathrm{tan}\:\theta \\ $$$$\Rightarrow\mathrm{2}{x}={y}\mathrm{cot}\:\alpha−\mathrm{2}{x}\mathrm{cot}\:\alpha\mathrm{tan}\:\theta \\ $$$$\Rightarrow\mathrm{2}{x}\left(\mathrm{1}+\mathrm{cot}\:\alpha\mathrm{tan}\:\theta\right)={y}\mathrm{cot}\:\alpha \\ $$$$\Rightarrow\frac{\mathrm{2}{x}}{{y}}=\frac{\mathrm{cot}\:\alpha}{\mathrm{1}+\mathrm{cot}\:\alpha\mathrm{tan}\:\theta}\:….\left(\mathrm{2}\right) \\ $$$${From}\:\left(\mathrm{1}\right)\:{and}\:\left(\mathrm{2}\right), \\ $$$$\mathrm{sin}\:\mathrm{2}\theta=\frac{\mathrm{cot}\:\alpha}{\mathrm{1}+\mathrm{cot}\:\alpha\mathrm{tan}\:\theta}\: \\ $$$$\mathrm{sin}\:\mathrm{2}\theta+\mathrm{cot}\:\alpha.\mathrm{2sin}\:^{\mathrm{2}} \theta=\mathrm{cot}\:\alpha \\ $$$$\mathrm{sin}\:\mathrm{2}\theta=\mathrm{cot}\:\alpha\left(\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} \theta\right) \\ $$$$\mathrm{sin}\:\mathrm{2}\theta=\mathrm{cot}\:\alpha.\mathrm{cos}\:\mathrm{2}\theta \\ $$$$\mathrm{tan}\:\mathrm{2}\theta=\mathrm{cot}\:\alpha \\ $$$${Q}.{E}.{D}. \\ $$
Commented by peter frank last updated on 21/Sep/18

$${thank}\:{you} \\ $$
