Question Number 44200 by Tawa1 last updated on 23/Sep/18

Commented by MJS last updated on 23/Sep/18
![A term1×term2=0 ⇔ term1=0 ∨ term2=0 e^x −e^π =0 ⇒ x=π e^x −π=0 ⇒ x=ln π B n=2k [⇒ n even] n^4 −n^3 +n^2 −n=16k^4 −8k^3 +4k^2 −2k= =2(8k^4 −4k^3 +2k^2 −k) which is divisible by 2 n=2k+1 [⇒ n uneven] n^4 −n^3 +n^2 +−n=16k^4 +24k^3 +16k^2 +4k= =4(4k^4 +6k^3 +4k^2 +k) which is divisible by 2 C ((4π)/3)r^3 =π^3 ⇒ r=(1/2)((6π^2 ))^(1/3) you can′t build this because there′s no exact value, neither for r nor for perimeter D log_2 (2^2 +5×2^2 ×3)=log_2 (2^2 (1+15))= =log_2 (2^2 ×2^4 )=log_2 2^6 =6 2log_3 2 +log_3 (7−(1/4))=2log_3 2 +log_3 ((27)/4)= =2log_3 2 +log_3 27 −log_3 4= =2log_3 2 +log_3 3^3 −log_3 2^2 = =2log_3 2 +3−2log_3 2 =3 (((log_2 128 −2)^3 )/(3+2))=(((log_2 2^7 −2)^3 )/5)=(((7−2)^3 )/5)=25 (−1)^(32+π^0 ) =(−1)^(32+1) =(−1)^(33) =−1 6×3+25−1=42 E area=rectangle+triangle rectangle=a×y triangle=((a×(x−y))/2) area=((a×(x+y))/2)](https://www.tinkutara.com/question/Q44203.png)
$${A} \\ $$$${term}\mathrm{1}×{term}\mathrm{2}=\mathrm{0}\:\Leftrightarrow\:{term}\mathrm{1}=\mathrm{0}\:\vee\:{term}\mathrm{2}=\mathrm{0} \\ $$$$\mathrm{e}^{{x}} −\mathrm{e}^{\pi} =\mathrm{0}\:\Rightarrow\:{x}=\pi \\ $$$$\mathrm{e}^{{x}} −\pi=\mathrm{0}\:\Rightarrow\:{x}=\mathrm{ln}\:\pi \\ $$$${B} \\ $$$${n}=\mathrm{2}{k}\:\left[\Rightarrow\:{n}\:\mathrm{even}\right] \\ $$$${n}^{\mathrm{4}} −{n}^{\mathrm{3}} +{n}^{\mathrm{2}} −{n}=\mathrm{16}{k}^{\mathrm{4}} −\mathrm{8}{k}^{\mathrm{3}} +\mathrm{4}{k}^{\mathrm{2}} −\mathrm{2}{k}= \\ $$$$=\mathrm{2}\left(\mathrm{8}{k}^{\mathrm{4}} −\mathrm{4}{k}^{\mathrm{3}} +\mathrm{2}{k}^{\mathrm{2}} −{k}\right)\:\mathrm{which}\:\mathrm{is}\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{2} \\ $$$${n}=\mathrm{2}{k}+\mathrm{1}\:\left[\Rightarrow\:{n}\:\mathrm{uneven}\right] \\ $$$${n}^{\mathrm{4}} −{n}^{\mathrm{3}} +{n}^{\mathrm{2}} +−{n}=\mathrm{16}{k}^{\mathrm{4}} +\mathrm{24}{k}^{\mathrm{3}} +\mathrm{16}{k}^{\mathrm{2}} +\mathrm{4}{k}= \\ $$$$=\mathrm{4}\left(\mathrm{4}{k}^{\mathrm{4}} +\mathrm{6}{k}^{\mathrm{3}} +\mathrm{4}{k}^{\mathrm{2}} +{k}\right)\:\mathrm{which}\:\mathrm{is}\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{2} \\ $$$${C} \\ $$$$\frac{\mathrm{4}\pi}{\mathrm{3}}{r}^{\mathrm{3}} =\pi^{\mathrm{3}} \:\Rightarrow\:{r}=\frac{\mathrm{1}}{\mathrm{2}}\sqrt[{\mathrm{3}}]{\mathrm{6}\pi^{\mathrm{2}} } \\ $$$$\mathrm{you}\:\mathrm{can}'\mathrm{t}\:\mathrm{build}\:\mathrm{this}\:\mathrm{because}\:\mathrm{there}'\mathrm{s}\:\mathrm{no}\:\mathrm{exact} \\ $$$$\mathrm{value},\:\mathrm{neither}\:\mathrm{for}\:{r}\:\mathrm{nor}\:\mathrm{for}\:\mathrm{perimeter} \\ $$$${D} \\ $$$$\mathrm{log}_{\mathrm{2}} \left(\mathrm{2}^{\mathrm{2}} +\mathrm{5}×\mathrm{2}^{\mathrm{2}} ×\mathrm{3}\right)=\mathrm{log}_{\mathrm{2}} \left(\mathrm{2}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{15}\right)\right)= \\ $$$$=\mathrm{log}_{\mathrm{2}} \left(\mathrm{2}^{\mathrm{2}} ×\mathrm{2}^{\mathrm{4}} \right)=\mathrm{log}_{\mathrm{2}} \:\mathrm{2}^{\mathrm{6}} =\mathrm{6} \\ $$$$\mathrm{2log}_{\mathrm{3}} \:\mathrm{2}\:+\mathrm{log}_{\mathrm{3}} \left(\mathrm{7}−\frac{\mathrm{1}}{\mathrm{4}}\right)=\mathrm{2log}_{\mathrm{3}} \:\mathrm{2}\:+\mathrm{log}_{\mathrm{3}} \:\frac{\mathrm{27}}{\mathrm{4}}= \\ $$$$=\mathrm{2log}_{\mathrm{3}} \:\mathrm{2}\:+\mathrm{log}_{\mathrm{3}} \:\mathrm{27}\:−\mathrm{log}_{\mathrm{3}} \:\mathrm{4}= \\ $$$$=\mathrm{2log}_{\mathrm{3}} \:\mathrm{2}\:+\mathrm{log}_{\mathrm{3}} \:\mathrm{3}^{\mathrm{3}} \:−\mathrm{log}_{\mathrm{3}} \:\mathrm{2}^{\mathrm{2}} = \\ $$$$=\mathrm{2log}_{\mathrm{3}} \:\mathrm{2}\:+\mathrm{3}−\mathrm{2log}_{\mathrm{3}} \:\mathrm{2}\:=\mathrm{3} \\ $$$$\frac{\left(\mathrm{log}_{\mathrm{2}} \:\mathrm{128}\:−\mathrm{2}\right)^{\mathrm{3}} }{\mathrm{3}+\mathrm{2}}=\frac{\left(\mathrm{log}_{\mathrm{2}} \:\mathrm{2}^{\mathrm{7}} \:−\mathrm{2}\right)^{\mathrm{3}} }{\mathrm{5}}=\frac{\left(\mathrm{7}−\mathrm{2}\right)^{\mathrm{3}} }{\mathrm{5}}=\mathrm{25} \\ $$$$\left(−\mathrm{1}\right)^{\mathrm{32}+\pi^{\mathrm{0}} } =\left(−\mathrm{1}\right)^{\mathrm{32}+\mathrm{1}} =\left(−\mathrm{1}\right)^{\mathrm{33}} =−\mathrm{1} \\ $$$$\mathrm{6}×\mathrm{3}+\mathrm{25}−\mathrm{1}=\mathrm{42} \\ $$$${E} \\ $$$$\mathrm{area}=\mathrm{rectangle}+\mathrm{triangle} \\ $$$$\mathrm{rectangle}={a}×{y} \\ $$$$\mathrm{triangle}=\frac{{a}×\left({x}−{y}\right)}{\mathrm{2}} \\ $$$$\mathrm{area}=\frac{{a}×\left({x}+{y}\right)}{\mathrm{2}} \\ $$
Commented by maxmathsup by imad last updated on 23/Sep/18
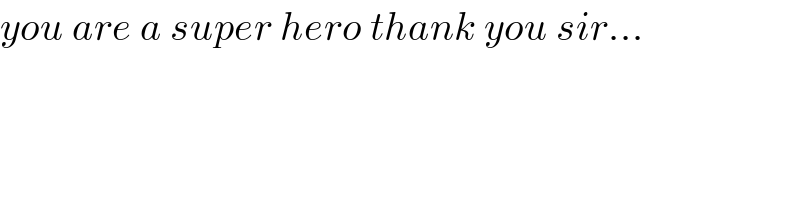
$${you}\:{are}\:{a}\:{super}\:{hero}\:{thank}\:{you}\:{sir}… \\ $$
Commented by Tawa1 last updated on 23/Sep/18

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{effort}. \\ $$
Commented by MJS last updated on 23/Sep/18

$$\mathrm{you}'\mathrm{re}\:\mathrm{welcome} \\ $$
