Question Number 44230 by behi83417@gmail.com last updated on 24/Sep/18
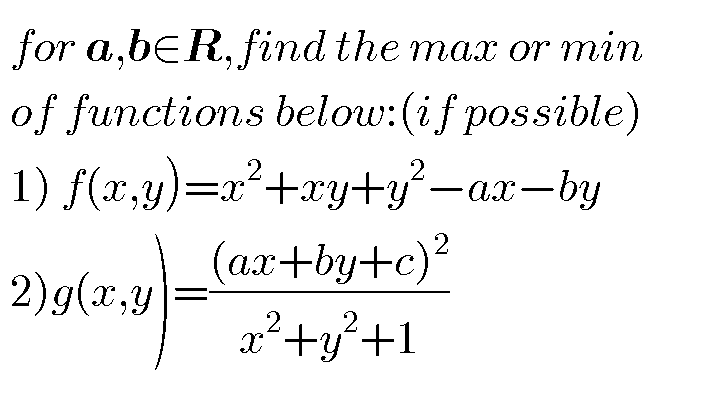
Answered by MrW3 last updated on 25/Sep/18
![(1) f(x,y)=x^2 +xy+y^2 −ax−by (∂f/∂x)=2x+y−a=0 ...(i) (∂f/∂y)=x+2y−b=0 ...(ii) 3x−2a+b=0 x=((2a−b)/3) 3y−2b+a=0 y=((2b−a)/3) f_(min) =(((2a−b)/3))^2 +(((2a−b)/3))(((2b−a)/3))+(((2b−a)/3))^2 −a(((2a−b)/3))−b(((2b−a)/3)) =(1/9)[4a^2 −4ab+b^2 +4ab−2b^2 −2a^2 +ab+4b^2 −4ab+a^2 −6a^2 +3ab−6b^2 +3ab] =(1/3)(ab−a^2 −b^2 ) (2) g(x,y)=(((ax+by+c)^2 )/(x^2 +y^2 +1)) (∂g/∂x)=−((2x(ax+by+c)^2 )/((x^2 +y^2 +1)^2 ))+((2a(ax+by+c))/(x^2 +y^2 +1))=0 x(ax+by+c)=a(x^2 +y^2 +1) ...(i) (∂g/∂y)=−((2y(ax+by+c)^2 )/((x^2 +y^2 +1)^2 ))+((2b(ax+by+c))/(x^2 +y^2 +1))=0 y(ax+by+c)=b(x^2 +y^2 +1) ...(ii) (x/a)=(y/b) x(ax+((b^2 x)/a)+c)=a(x^2 +((b^2 x^2 )/a^2 )+1) ax(a^2 x+b^2 x+ac)=a(a^2 x^2 +b^2 x^2 +a^2 ) ⇒x=(a/c) ⇒y=(b/c) ⇒g_(max) =((((a^2 /c)+(b^2 /c)+c)^2 )/((a^2 /c^2 )+(b^2 /c^2 )+1))=a^2 +b^2 +c^2](https://www.tinkutara.com/question/Q44256.png)
$$\left(\mathrm{1}\right) \\ $$$${f}\left({x},{y}\right)={x}^{\mathrm{2}} +{xy}+{y}^{\mathrm{2}} −{ax}−{by} \\ $$$$\frac{\partial{f}}{\partial{x}}=\mathrm{2}{x}+{y}−{a}=\mathrm{0}\:\:…\left({i}\right) \\ $$$$\frac{\partial{f}}{\partial{y}}={x}+\mathrm{2}{y}−{b}=\mathrm{0}\:\:…\left({ii}\right) \\ $$$$\mathrm{3}{x}−\mathrm{2}{a}+{b}=\mathrm{0} \\ $$$${x}=\frac{\mathrm{2}{a}−{b}}{\mathrm{3}} \\ $$$$\mathrm{3}{y}−\mathrm{2}{b}+{a}=\mathrm{0} \\ $$$${y}=\frac{\mathrm{2}{b}−{a}}{\mathrm{3}} \\ $$$${f}_{{min}} =\left(\frac{\mathrm{2}{a}−{b}}{\mathrm{3}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{2}{a}−{b}}{\mathrm{3}}\right)\left(\frac{\mathrm{2}{b}−{a}}{\mathrm{3}}\right)+\left(\frac{\mathrm{2}{b}−{a}}{\mathrm{3}}\right)^{\mathrm{2}} −{a}\left(\frac{\mathrm{2}{a}−{b}}{\mathrm{3}}\right)−{b}\left(\frac{\mathrm{2}{b}−{a}}{\mathrm{3}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{9}}\left[\mathrm{4}{a}^{\mathrm{2}} −\mathrm{4}{ab}+{b}^{\mathrm{2}} +\mathrm{4}{ab}−\mathrm{2}{b}^{\mathrm{2}} −\mathrm{2}{a}^{\mathrm{2}} +{ab}+\mathrm{4}{b}^{\mathrm{2}} −\mathrm{4}{ab}+{a}^{\mathrm{2}} −\mathrm{6}{a}^{\mathrm{2}} +\mathrm{3}{ab}−\mathrm{6}{b}^{\mathrm{2}} +\mathrm{3}{ab}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left({ab}−{a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right) \\ $$$$ \\ $$$$\left(\mathrm{2}\right) \\ $$$${g}\left({x},{y}\right)=\frac{\left({ax}+{by}+{c}\right)^{\mathrm{2}} }{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\frac{\partial{g}}{\partial{x}}=−\frac{\mathrm{2}{x}\left({ax}+{by}+{c}\right)^{\mathrm{2}} }{\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{2}{a}\left({ax}+{by}+{c}\right)}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{1}}=\mathrm{0} \\ $$$${x}\left({ax}+{by}+{c}\right)={a}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{1}\right)\:\:…\left({i}\right) \\ $$$$\frac{\partial{g}}{\partial{y}}=−\frac{\mathrm{2}{y}\left({ax}+{by}+{c}\right)^{\mathrm{2}} }{\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{2}{b}\left({ax}+{by}+{c}\right)}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{1}}=\mathrm{0} \\ $$$${y}\left({ax}+{by}+{c}\right)={b}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{1}\right)\:\:…\left({ii}\right) \\ $$$$\frac{{x}}{{a}}=\frac{{y}}{{b}} \\ $$$${x}\left({ax}+\frac{{b}^{\mathrm{2}} {x}}{{a}}+{c}\right)={a}\left({x}^{\mathrm{2}} +\frac{{b}^{\mathrm{2}} {x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\mathrm{1}\right)\: \\ $$$${ax}\left({a}^{\mathrm{2}} {x}+{b}^{\mathrm{2}} {x}+{ac}\right)={a}\left({a}^{\mathrm{2}} {x}^{\mathrm{2}} +{b}^{\mathrm{2}} {x}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)\: \\ $$$$\Rightarrow{x}=\frac{{a}}{{c}} \\ $$$$\Rightarrow{y}=\frac{{b}}{{c}} \\ $$$$\Rightarrow{g}_{{max}} =\frac{\left(\frac{{a}^{\mathrm{2}} }{{c}}+\frac{{b}^{\mathrm{2}} }{{c}}+{c}\right)^{\mathrm{2}} }{\frac{{a}^{\mathrm{2}} }{{c}^{\mathrm{2}} }+\frac{{b}^{\mathrm{2}} }{{c}^{\mathrm{2}} }+\mathrm{1}}={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \\ $$
Commented by behi83417@gmail.com last updated on 25/Sep/18

$${thank}\:{you}\:{dear}\:{master}. \\ $$$${nice}\:{work}\:{done}\:{by}\:{you}.{perfect}! \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 25/Sep/18
$${bah}…{darun}…{excellent}… \\ $$
Commented by MrW3 last updated on 25/Sep/18
$${thank}\:{you}\:{both}\:{sirs}! \\ $$
Commented by rahul 19 last updated on 26/Sep/18
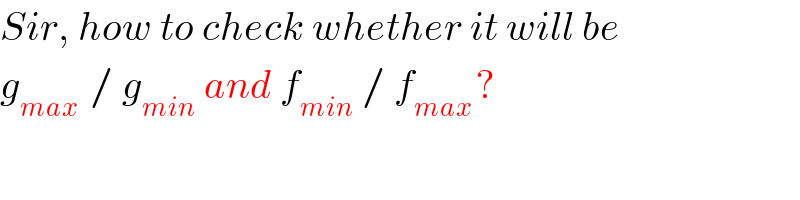
$${Sir},\:{how}\:{to}\:{check}\:{whether}\:{it}\:{will}\:{be} \\ $$$${g}_{{max}\:} \:/\:{g}_{{min}} \:{and}\:{f}_{{min}} \:/\:{f}_{{max}\:} ? \\ $$
Commented by MrW3 last updated on 26/Sep/18
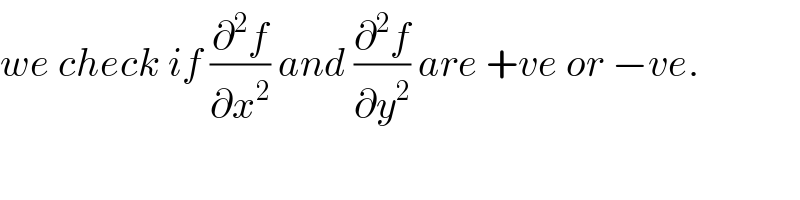
$${we}\:{check}\:{if}\:\frac{\partial^{\mathrm{2}} {f}}{\partial{x}^{\mathrm{2}} }\:{and}\:\frac{\partial^{\mathrm{2}} {f}}{\partial{y}^{\mathrm{2}} }\:{are}\:+{ve}\:{or}\:−{ve}. \\ $$
Commented by rahul 19 last updated on 26/Sep/18
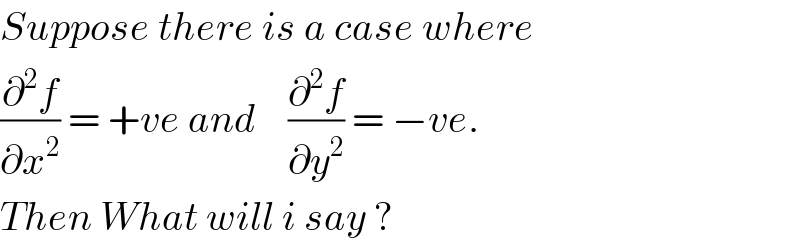
$${Suppose}\:{there}\:{is}\:{a}\:{case}\:{where} \\ $$$$\frac{\partial^{\mathrm{2}} {f}}{\partial{x}^{\mathrm{2}} }\:=\:+{ve}\:{and}\:\:\:\:\frac{\partial^{\mathrm{2}} {f}}{\partial{y}^{\mathrm{2}} }\:=\:−{ve}.\: \\ $$$${Then}\:{What}\:{will}\:{i}\:{say}\:? \\ $$
Commented by MrW3 last updated on 26/Sep/18

$${max}.\:{in}\:{y}−{direction}\:{but} \\ $$$${min}.\:{in}\:{x}−{direction} \\ $$$$\Rightarrow{neither}\:{a}\:{max}.\:{nor}\:{a}\:{min}.\:{for} \\ $$$${the}\:{function} \\ $$
Commented by rahul 19 last updated on 26/Sep/18

$${Ok}\:{sir},\:{thanks}! \\ $$
