Question Number 44395 by ajfour last updated on 28/Sep/18

Commented by ajfour last updated on 28/Sep/18
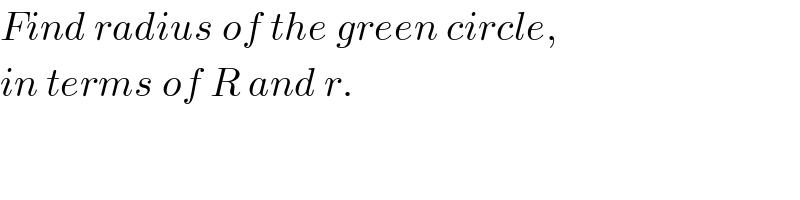
$${Find}\:{radius}\:{of}\:{the}\:{green}\:{circle}, \\ $$$${in}\:{terms}\:{of}\:{R}\:{and}\:{r}. \\ $$
Commented by ajfour last updated on 28/Sep/18

Commented by ajfour last updated on 28/Sep/18
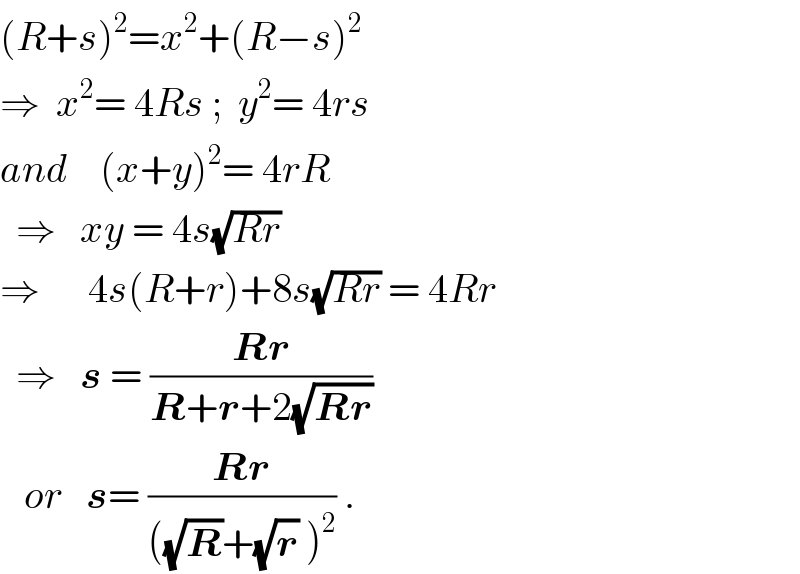
$$\left({R}+{s}\right)^{\mathrm{2}} ={x}^{\mathrm{2}} +\left({R}−{s}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\:{x}^{\mathrm{2}} =\:\mathrm{4}{Rs}\:;\:\:{y}^{\mathrm{2}} =\:\mathrm{4}{rs} \\ $$$${and}\:\:\:\:\left({x}+{y}\right)^{\mathrm{2}} =\:\mathrm{4}{rR} \\ $$$$\:\:\Rightarrow\:\:\:{xy}\:=\:\mathrm{4}{s}\sqrt{{Rr}} \\ $$$$\Rightarrow\:\:\:\:\:\:\mathrm{4}{s}\left({R}+{r}\right)+\mathrm{8}{s}\sqrt{{Rr}}\:=\:\mathrm{4}{Rr} \\ $$$$\:\:\Rightarrow\:\:\:\boldsymbol{{s}}\:=\:\frac{\boldsymbol{{Rr}}}{\boldsymbol{{R}}+\boldsymbol{{r}}+\mathrm{2}\sqrt{\boldsymbol{{Rr}}}} \\ $$$$\:\:\:{or}\:\:\:\boldsymbol{{s}}=\:\frac{\boldsymbol{{Rr}}}{\left(\sqrt{\boldsymbol{{R}}}+\sqrt{\boldsymbol{{r}}}\:\right)^{\mathrm{2}} }\:. \\ $$
Answered by rahul 19 last updated on 28/Sep/18
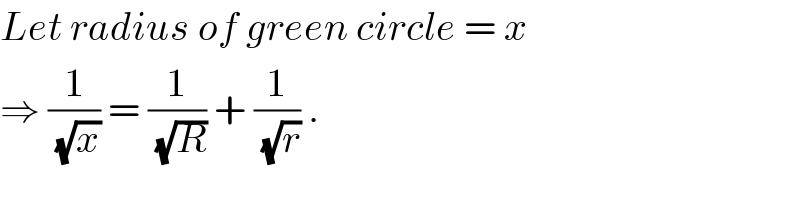
$${Let}\:{radius}\:{of}\:{green}\:{circle}\:=\:{x} \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{\:\sqrt{{x}}}\:=\:\frac{\mathrm{1}}{\:\sqrt{{R}}}\:+\:\frac{\mathrm{1}}{\:\sqrt{{r}}}\:. \\ $$
Commented by ajfour last updated on 28/Sep/18
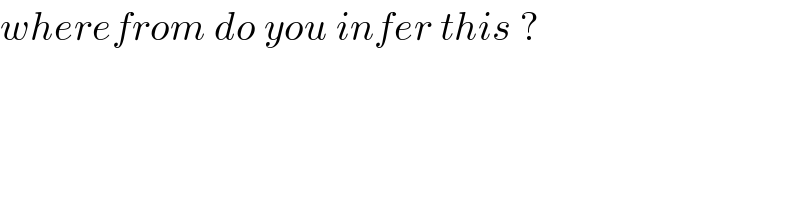
$${wherefrom}\:{do}\:{you}\:{infer}\:{this}\:? \\ $$
Commented by rahul 19 last updated on 28/Sep/18
$${Sir},\:{you}\:{have}\:{posted}\:{the}\:{same}\:{Q}.\:{some} \\ $$$${time}\:{back}\:{and}\:{that}\:{time}\:{i}\:{gave}\:{a}\:{proof} \\ $$$$\left.{also}\:,\:{i}\:{remembered}\:{the}\:{result}\::\right) \\ $$
Commented by ajfour last updated on 28/Sep/18

$${seems}\:{likely}.. \\ $$
