Menu Close

Question-44436

Tinku Tara 0 Comments
Pin




Question Number 44436 by ajfour last updated on 29/Sep/18
Commented by ajfour last updated on 29/Sep/18
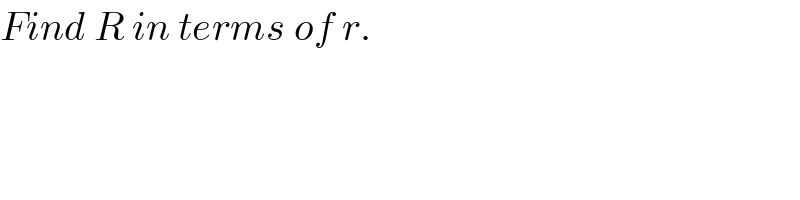
Find R in terms of r.
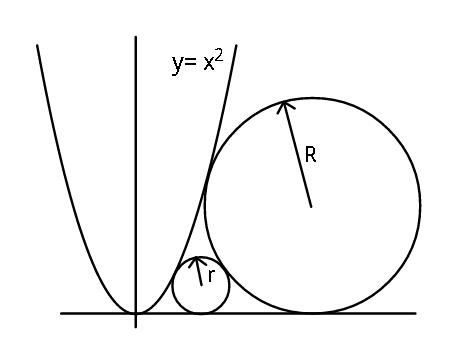
$${Find}\:{R}\:{in}\:{terms}\:{of}\:{r}. \\ $$
Answered by MrW3 last updated on 29/Sep/18
Commented by MrW3 last updated on 29/Sep/18
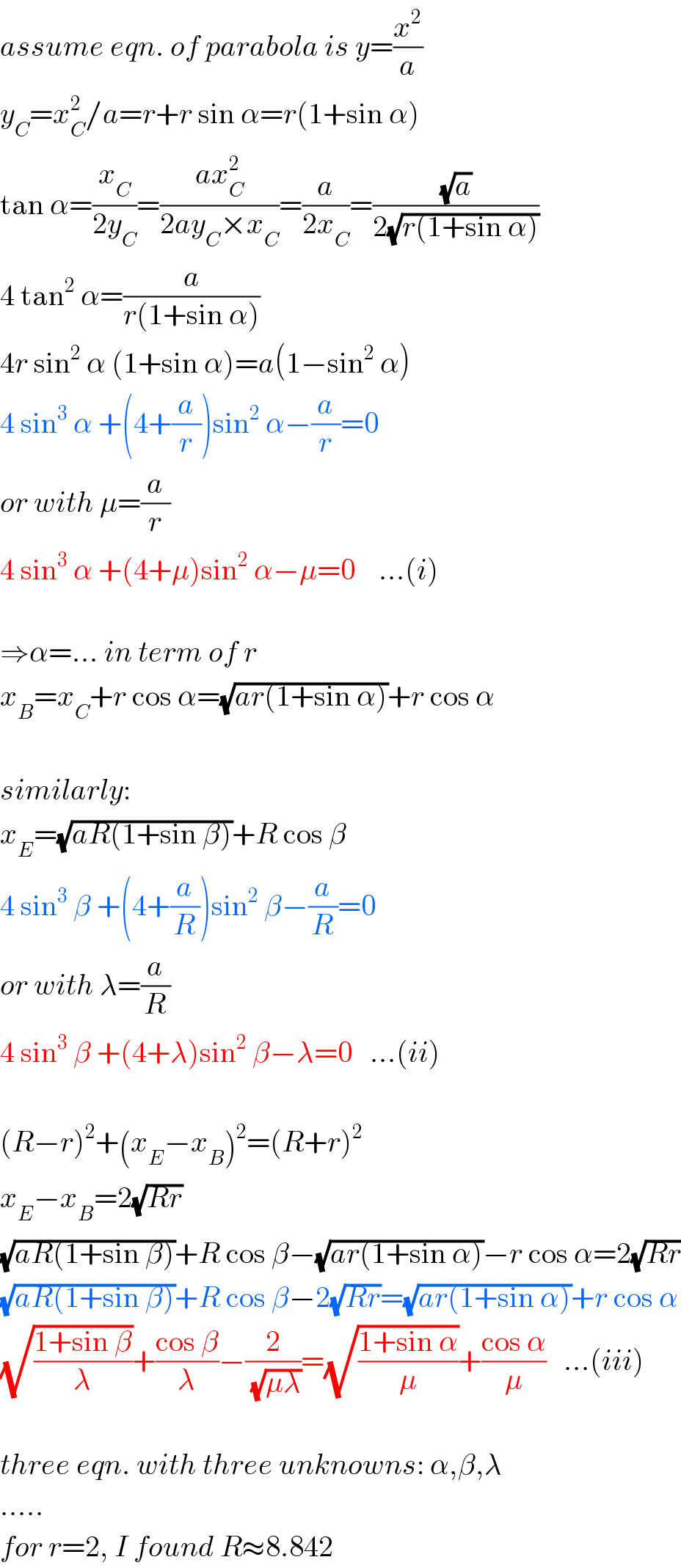
assume eqn. of parabola is y=(x^2 /a) y_C =x_C ^2 /a=r+r sin α=r(1+sin α) tan α=(x_C /(2y_C ))=((ax_C ^2 )/(2ay_C ×x_C ))=(a/(2x_C ))=((√a)/(2(√(r(1+sin α))))) 4 tan^2 α=(a/(r(1+sin α))) 4r sin^2 α (1+sin α)=a(1−sin^2 α) 4 sin^3 α +(4+(a/r))sin^2 α−(a/r)=0 or with μ=(a/r) 4 sin^3 α +(4+μ)sin^2 α−μ=0 ...(i) ⇒α=... in term of r x_B =x_C +r cos α=(√(ar(1+sin α)))+r cos α similarly: x_E =(√(aR(1+sin β)))+R cos β 4 sin^3 β +(4+(a/R))sin^2 β−(a/R)=0 or with λ=(a/R) 4 sin^3 β +(4+λ)sin^2 β−λ=0 ...(ii) (R−r)^2 +(x_E −x_B )^2 =(R+r)^2 x_E −x_B =2(√(Rr)) (√(aR(1+sin β)))+R cos β−(√(ar(1+sin α)))−r cos α=2(√(Rr)) (√(aR(1+sin β)))+R cos β−2(√(Rr))=(√(ar(1+sin α)))+r cos α (√((1+sin β)/λ))+((cos β)/λ)−(2/( (√(μλ))))=(√((1+sin α)/μ))+((cos α)/μ) ...(iii) three eqn. with three unknowns: α,β,λ ..... for r=2, I found R≈8.842
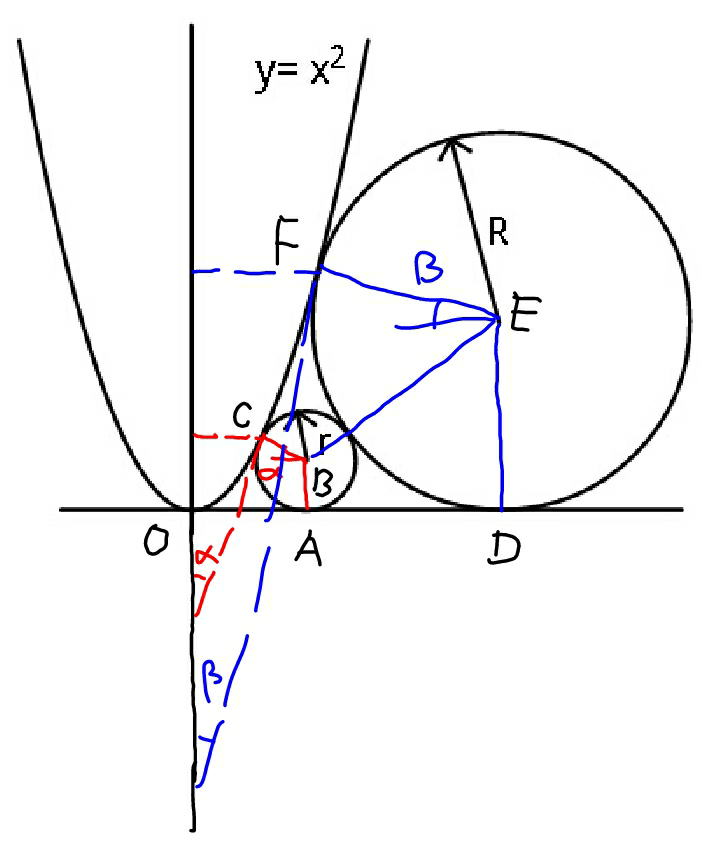
$${assume}\:{eqn}.\:{of}\:{parabola}\:{is}\:{y}=\frac{{x}^{\mathrm{2}} }{{a}} \\ $$$${y}_{{C}} ={x}_{{C}} ^{\mathrm{2}} /{a}={r}+{r}\:\mathrm{sin}\:\alpha={r}\left(\mathrm{1}+\mathrm{sin}\:\alpha\right) \\ $$$$\mathrm{tan}\:\alpha=\frac{{x}_{{C}} }{\mathrm{2}{y}_{{C}} }=\frac{{ax}_{{C}} ^{\mathrm{2}} }{\mathrm{2}{ay}_{{C}} ×{x}_{{C}} }=\frac{{a}}{\mathrm{2}{x}_{{C}} }=\frac{\sqrt{{a}}}{\mathrm{2}\sqrt{{r}\left(\mathrm{1}+\mathrm{sin}\:\alpha\right)}} \\ $$$$\mathrm{4}\:\mathrm{tan}^{\mathrm{2}} \:\alpha=\frac{{a}}{{r}\left(\mathrm{1}+\mathrm{sin}\:\alpha\right)} \\ $$$$\mathrm{4}{r}\:\mathrm{sin}^{\mathrm{2}} \:\alpha\:\left(\mathrm{1}+\mathrm{sin}\:\alpha\right)={a}\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:\alpha\right) \\ $$$$\mathrm{4}\:\mathrm{sin}^{\mathrm{3}} \:\alpha\:+\left(\mathrm{4}+\frac{{a}}{{r}}\right)\mathrm{sin}^{\mathrm{2}} \:\alpha−\frac{{a}}{{r}}=\mathrm{0} \\ $$$${or}\:{with}\:\mu=\frac{{a}}{{r}} \\ $$$$\mathrm{4}\:\mathrm{sin}^{\mathrm{3}} \:\alpha\:+\left(\mathrm{4}+\mu\right)\mathrm{sin}^{\mathrm{2}} \:\alpha−\mu=\mathrm{0}\:\:\:\:…\left({i}\right) \\ $$$$ \\ $$$$\Rightarrow\alpha=…\:{in}\:{term}\:{of}\:{r} \\ $$$${x}_{{B}} ={x}_{{C}} +{r}\:\mathrm{cos}\:\alpha=\sqrt{{ar}\left(\mathrm{1}+\mathrm{sin}\:\alpha\right)}+{r}\:\mathrm{cos}\:\alpha \\ $$$$ \\ $$$${similarly}: \\ $$$${x}_{{E}} =\sqrt{{aR}\left(\mathrm{1}+\mathrm{sin}\:\beta\right)}+{R}\:\mathrm{cos}\:\beta \\ $$$$\mathrm{4}\:\mathrm{sin}^{\mathrm{3}} \:\beta\:+\left(\mathrm{4}+\frac{{a}}{{R}}\right)\mathrm{sin}^{\mathrm{2}} \:\beta−\frac{{a}}{{R}}=\mathrm{0} \\ $$$${or}\:{with}\:\lambda=\frac{{a}}{{R}} \\ $$$$\mathrm{4}\:\mathrm{sin}^{\mathrm{3}} \:\beta\:+\left(\mathrm{4}+\lambda\right)\mathrm{sin}^{\mathrm{2}} \:\beta−\lambda=\mathrm{0}\:\:\:…\left({ii}\right) \\ $$$$ \\ $$$$\left({R}−{r}\right)^{\mathrm{2}} +\left({x}_{{E}} −{x}_{{B}} \right)^{\mathrm{2}} =\left({R}+{r}\right)^{\mathrm{2}} \\ $$$${x}_{{E}} −{x}_{{B}} =\mathrm{2}\sqrt{{Rr}} \\ $$$$\sqrt{{aR}\left(\mathrm{1}+\mathrm{sin}\:\beta\right)}+{R}\:\mathrm{cos}\:\beta−\sqrt{{ar}\left(\mathrm{1}+\mathrm{sin}\:\alpha\right)}−{r}\:\mathrm{cos}\:\alpha=\mathrm{2}\sqrt{{Rr}} \\ $$$$\sqrt{{aR}\left(\mathrm{1}+\mathrm{sin}\:\beta\right)}+{R}\:\mathrm{cos}\:\beta−\mathrm{2}\sqrt{{Rr}}=\sqrt{{ar}\left(\mathrm{1}+\mathrm{sin}\:\alpha\right)}+{r}\:\mathrm{cos}\:\alpha \\ $$$$\sqrt{\frac{\mathrm{1}+\mathrm{sin}\:\beta}{\lambda}}+\frac{\mathrm{cos}\:\beta}{\lambda}−\frac{\mathrm{2}}{\:\sqrt{\mu\lambda}}=\sqrt{\frac{\mathrm{1}+\mathrm{sin}\:\alpha}{\mu}}+\frac{\mathrm{cos}\:\alpha}{\mu}\:\:\:…\left({iii}\right) \\ $$$$ \\ $$$${three}\:{eqn}.\:{with}\:{three}\:{unknowns}:\:\alpha,\beta,\lambda \\ $$$$….. \\ $$$${for}\:{r}=\mathrm{2},\:{I}\:{found}\:{R}\approx\mathrm{8}.\mathrm{842} \\ $$
Commented by ajfour last updated on 29/Sep/18
great way sir, very nice, thanks.
$${great}\:{way}\:{sir},\:{very}\:{nice},\:{thanks}. \\ $$
Commented by ajfour last updated on 29/Sep/18
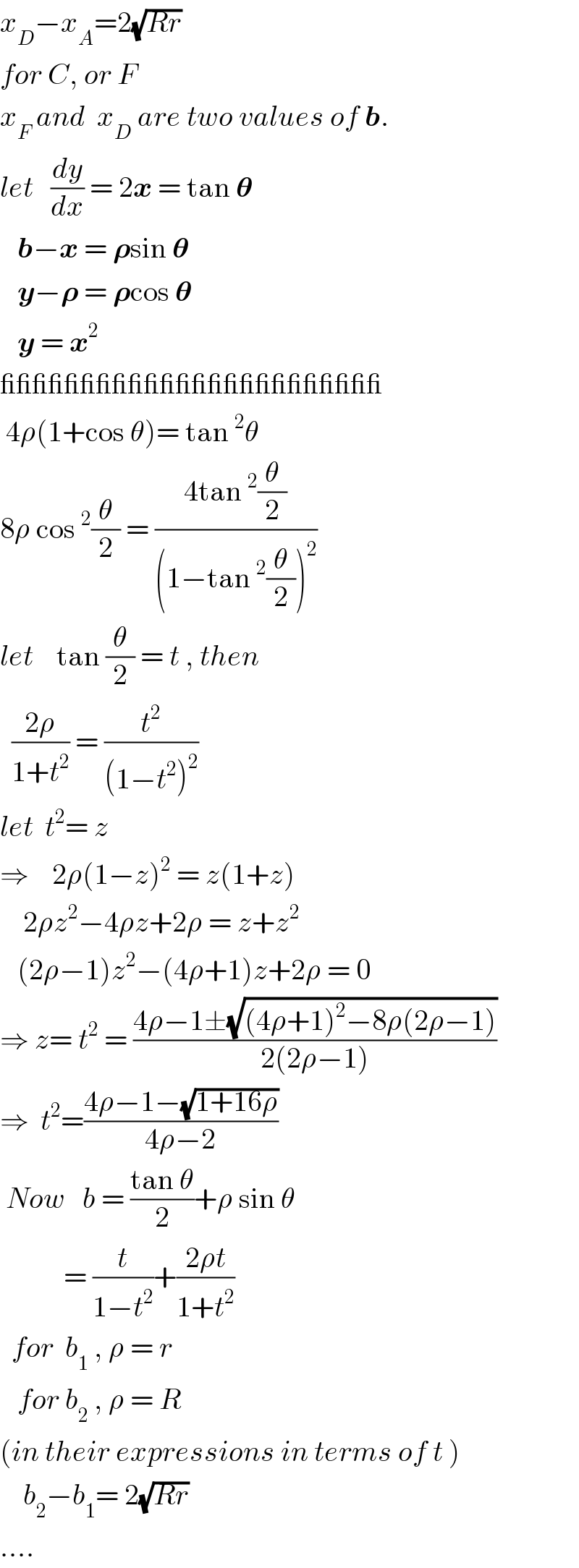
x_D −x_A =2(√(Rr)) for C, or F x_F and x_D are two values of b. let (dy/dx) = 2x = tan 𝛉 b−x = 𝛒sin 𝛉 y−𝛒 = 𝛒cos 𝛉 y = x^2 ________________________ 4ρ(1+cos θ)= tan^2 θ 8ρ cos^2 (θ/2) = ((4tan^2 (θ/2))/((1−tan^2 (θ/2))^2 )) let tan (θ/2) = t , then ((2ρ)/(1+t^2 )) = (t^2 /((1−t^2 )^2 )) let t^2 = z ⇒ 2ρ(1−z)^2 = z(1+z) 2ρz^2 −4ρz+2ρ = z+z^2 (2ρ−1)z^2 −(4ρ+1)z+2ρ = 0 ⇒ z= t^2 = ((4ρ−1±(√((4ρ+1)^2 −8ρ(2ρ−1))))/(2(2ρ−1))) ⇒ t^2 =((4ρ−1−(√(1+16ρ)))/(4ρ−2)) Now b = ((tan θ)/2)+ρ sin θ = (t/(1−t^2 ))+((2ρt)/(1+t^2 )) for b_1 , ρ = r for b_2 , ρ = R (in their expressions in terms of t ) b_2 −b_1 = 2(√(Rr)) ....
$${x}_{{D}} −{x}_{{A}} =\mathrm{2}\sqrt{{Rr}} \\ $$$${for}\:{C},\:{or}\:{F} \\ $$$${x}_{{F}} \:{and}\:\:{x}_{{D}} \:{are}\:{two}\:{values}\:{of}\:\boldsymbol{{b}}. \\ $$$${let}\:\:\:\frac{{dy}}{{dx}}\:=\:\mathrm{2}\boldsymbol{{x}}\:=\:\mathrm{tan}\:\boldsymbol{\theta} \\ $$$$\:\:\:\boldsymbol{{b}}−\boldsymbol{{x}}\:=\:\boldsymbol{\rho}\mathrm{sin}\:\boldsymbol{\theta} \\ $$$$\:\:\:\boldsymbol{{y}}−\boldsymbol{\rho}\:=\:\boldsymbol{\rho}\mathrm{cos}\:\boldsymbol{\theta} \\ $$$$\:\:\:\boldsymbol{{y}}\:=\:\boldsymbol{{x}}^{\mathrm{2}} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\:\mathrm{4}\rho\left(\mathrm{1}+\mathrm{cos}\:\theta\right)=\:\mathrm{tan}\:^{\mathrm{2}} \theta \\ $$$$\mathrm{8}\rho\:\mathrm{cos}\:^{\mathrm{2}} \frac{\theta}{\mathrm{2}}\:=\:\frac{\mathrm{4tan}\:^{\mathrm{2}} \frac{\theta}{\mathrm{2}}}{\left(\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \frac{\theta}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$${let}\:\:\:\:\mathrm{tan}\:\frac{\theta}{\mathrm{2}}\:=\:{t}\:,\:{then} \\ $$$$\:\:\frac{\mathrm{2}\rho}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\:\frac{{t}^{\mathrm{2}} }{\left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$${let}\:\:{t}^{\mathrm{2}} =\:{z} \\ $$$$\Rightarrow\:\:\:\:\mathrm{2}\rho\left(\mathrm{1}−{z}\right)^{\mathrm{2}} \:=\:{z}\left(\mathrm{1}+{z}\right) \\ $$$$\:\:\:\:\mathrm{2}\rho{z}^{\mathrm{2}} −\mathrm{4}\rho{z}+\mathrm{2}\rho\:=\:{z}+{z}^{\mathrm{2}} \\ $$$$\:\:\:\left(\mathrm{2}\rho−\mathrm{1}\right){z}^{\mathrm{2}} −\left(\mathrm{4}\rho+\mathrm{1}\right){z}+\mathrm{2}\rho\:=\:\mathrm{0} \\ $$$$\Rightarrow\:{z}=\:{t}^{\mathrm{2}} \:=\:\frac{\mathrm{4}\rho−\mathrm{1}\pm\sqrt{\left(\mathrm{4}\rho+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{8}\rho\left(\mathrm{2}\rho−\mathrm{1}\right)}}{\mathrm{2}\left(\mathrm{2}\rho−\mathrm{1}\right)} \\ $$$$\Rightarrow\:\:{t}^{\mathrm{2}} =\frac{\mathrm{4}\rho−\mathrm{1}−\sqrt{\mathrm{1}+\mathrm{16}\rho}}{\mathrm{4}\rho−\mathrm{2}} \\ $$$$\:{Now}\:\:\:{b}\:=\:\frac{\mathrm{tan}\:\theta}{\mathrm{2}}+\rho\:\mathrm{sin}\:\theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:\frac{{t}}{\mathrm{1}−{t}^{\mathrm{2}} }+\frac{\mathrm{2}\rho{t}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$\:\:{for}\:\:{b}_{\mathrm{1}} \:,\:\rho\:=\:{r} \\ $$$$\:\:\:{for}\:{b}_{\mathrm{2}} \:,\:\rho\:=\:{R} \\ $$$$\left({in}\:{their}\:{expressions}\:{in}\:{terms}\:{of}\:{t}\:\right) \\ $$$$\:\:\:\:{b}_{\mathrm{2}} −{b}_{\mathrm{1}} =\:\mathrm{2}\sqrt{{Rr}} \\ $$$$…. \\ $$
Commented by MrW3 last updated on 29/Sep/18
Finding a direct expression for θ in term of R (and r), that′s great sir!
$${Finding}\:{a}\:{direct}\:{expression}\:{for}\:\theta\:{in} \\ $$$${term}\:{of}\:{R}\:\left({and}\:{r}\right),\:{that}'{s}\:{great}\:{sir}! \\ $$
Commented by ajfour last updated on 29/Sep/18
i have changed it entirely sir, its all just the same (parametric). probably, implicit as well.
$${i}\:{have}\:{changed}\:{it}\:{entirely}\:{sir}, \\ $$$${its}\:{all}\:{just}\:{the}\:{same}\:\left({parametric}\right). \\ $$$${probably},\:{implicit}\:{as}\:{well}. \\ $$
Commented by behi83417@gmail.com last updated on 29/Sep/18
nice work done!thanks master sir mrW3.
$${nice}\:{work}\:{done}!{thanks}\:{master} \\ $$$${sir}\:{mrW}\mathrm{3}. \\ $$
Commented by behi83417@gmail.com last updated on 29/Sep/18
sir Ajfour! great question & also nice prof.thanks for your nice viewpoint.
$${sir}\:{Ajfour}!\:{great}\:{question}\:\&\:{also} \\ $$$${nice}\:{prof}.{thanks}\:{for}\:{your}\:{nice} \\ $$$${viewpoint}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *