Menu Close

Question-44527

Tinku Tara 0 Comments
Pin




Question Number 44527 by Necxx last updated on 30/Sep/18
Commented by Necxx last updated on 30/Sep/18
21 please
$$\mathrm{21}\:{please} \\ $$
Commented by maxmathsup by imad last updated on 30/Sep/18
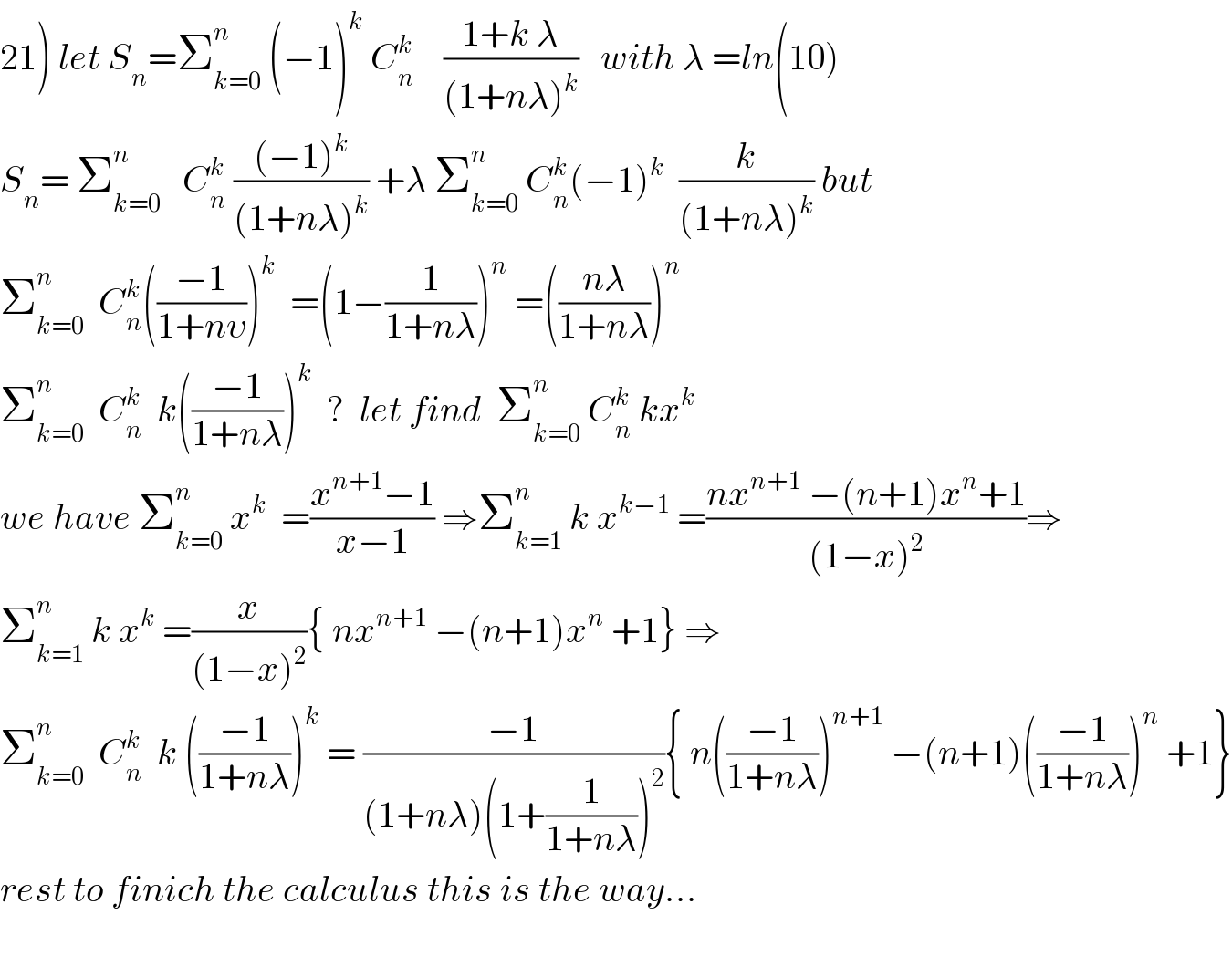
21) let S_n =Σ_(k=0) ^n (−1)^k C_n ^k ((1+k λ)/((1+nλ)^k )) with λ =ln(10) S_n = Σ_(k=0) ^n C_n ^k (((−1)^k )/((1+nλ)^k )) +λ Σ_(k=0) ^n C_n ^k (−1)^k (k/((1+nλ)^k )) but Σ_(k=0) ^n C_n ^k (((−1)/(1+nυ)))^k =(1−(1/(1+nλ)))^n =(((nλ)/(1+nλ)))^n Σ_(k=0) ^n C_n ^k k(((−1)/(1+nλ)))^k ? let find Σ_(k=0) ^n C_n ^k kx^k we have Σ_(k=0) ^n x^k =((x^(n+1) −1)/(x−1)) ⇒Σ_(k=1) ^n k x^(k−1) =((nx^(n+1) −(n+1)x^n +1)/((1−x)^2 ))⇒ Σ_(k=1) ^n k x^k =(x/((1−x)^2 )){ nx^(n+1) −(n+1)x^n +1} ⇒ Σ_(k=0) ^n C_n ^k k (((−1)/(1+nλ)))^k = ((−1)/((1+nλ)(1+(1/(1+nλ)))^2 )){ n(((−1)/(1+nλ)))^(n+1) −(n+1)(((−1)/(1+nλ)))^n +1} rest to finich the calculus this is the way...
$$\left.\mathrm{21}\right)\:{let}\:{S}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}} \:\left(−\mathrm{1}\right)^{{k}} \:{C}_{{n}} ^{{k}} \:\:\:\:\frac{\mathrm{1}+{k}\:\lambda}{\left(\mathrm{1}+{n}\lambda\right)^{{k}} }\:\:\:{with}\:\lambda\:={ln}\left(\mathrm{10}\right) \\ $$$${S}_{{n}} =\:\sum_{{k}=\mathrm{0}} ^{{n}} \:\:\:{C}_{{n}} ^{{k}} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{\left(\mathrm{1}+{n}\lambda\right)^{{k}} }\:+\lambda\:\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \left(−\mathrm{1}\right)^{{k}} \:\:\frac{{k}}{\left(\mathrm{1}+{n}\lambda\right)^{{k}} }\:{but} \\ $$$$\sum_{{k}=\mathrm{0}} ^{{n}} \:\:{C}_{{n}} ^{{k}} \left(\frac{−\mathrm{1}}{\mathrm{1}+{n}\upsilon}\right)^{{k}} \:\:=\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+{n}\lambda}\right)^{{n}} \:=\left(\frac{{n}\lambda}{\mathrm{1}+{n}\lambda}\right)^{{n}} \\ $$$$\sum_{{k}=\mathrm{0}} ^{{n}} \:\:{C}_{{n}} ^{{k}} \:\:{k}\left(\frac{−\mathrm{1}}{\mathrm{1}+{n}\lambda}\right)^{{k}} \:\:?\:\:{let}\:{find}\:\:\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:{kx}^{{k}} \:\:\: \\ $$$${we}\:{have}\:\sum_{{k}=\mathrm{0}} ^{{n}} \:{x}^{{k}} \:\:=\frac{{x}^{{n}+\mathrm{1}} −\mathrm{1}}{{x}−\mathrm{1}}\:\Rightarrow\sum_{{k}=\mathrm{1}} ^{{n}} \:{k}\:{x}^{{k}−\mathrm{1}} \:=\frac{{nx}^{{n}+\mathrm{1}} \:−\left({n}+\mathrm{1}\right){x}^{{n}} +\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }\Rightarrow \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} \:{k}\:{x}^{{k}} \:=\frac{{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }\left\{\:{nx}^{{n}+\mathrm{1}} \:−\left({n}+\mathrm{1}\right){x}^{{n}} \:+\mathrm{1}\right\}\:\Rightarrow \\ $$$$\sum_{{k}=\mathrm{0}} ^{{n}} \:\:{C}_{{n}} ^{{k}} \:\:{k}\:\left(\frac{−\mathrm{1}}{\mathrm{1}+{n}\lambda}\right)^{{k}} \:=\:\frac{−\mathrm{1}}{\left(\mathrm{1}+{n}\lambda\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}+{n}\lambda}\right)^{\mathrm{2}} }\left\{\:{n}\left(\frac{−\mathrm{1}}{\mathrm{1}+{n}\lambda}\right)^{{n}+\mathrm{1}} \:−\left({n}+\mathrm{1}\right)\left(\frac{−\mathrm{1}}{\mathrm{1}+{n}\lambda}\right)^{{n}} \:+\mathrm{1}\right\} \\ $$$${rest}\:{to}\:{finich}\:{the}\:{calculus}\:{this}\:{is}\:{the}\:{way}… \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *