Question Number 44557 by ajfour last updated on 01/Oct/18

Commented by ajfour last updated on 01/Oct/18

Commented by ajfour last updated on 01/Oct/18
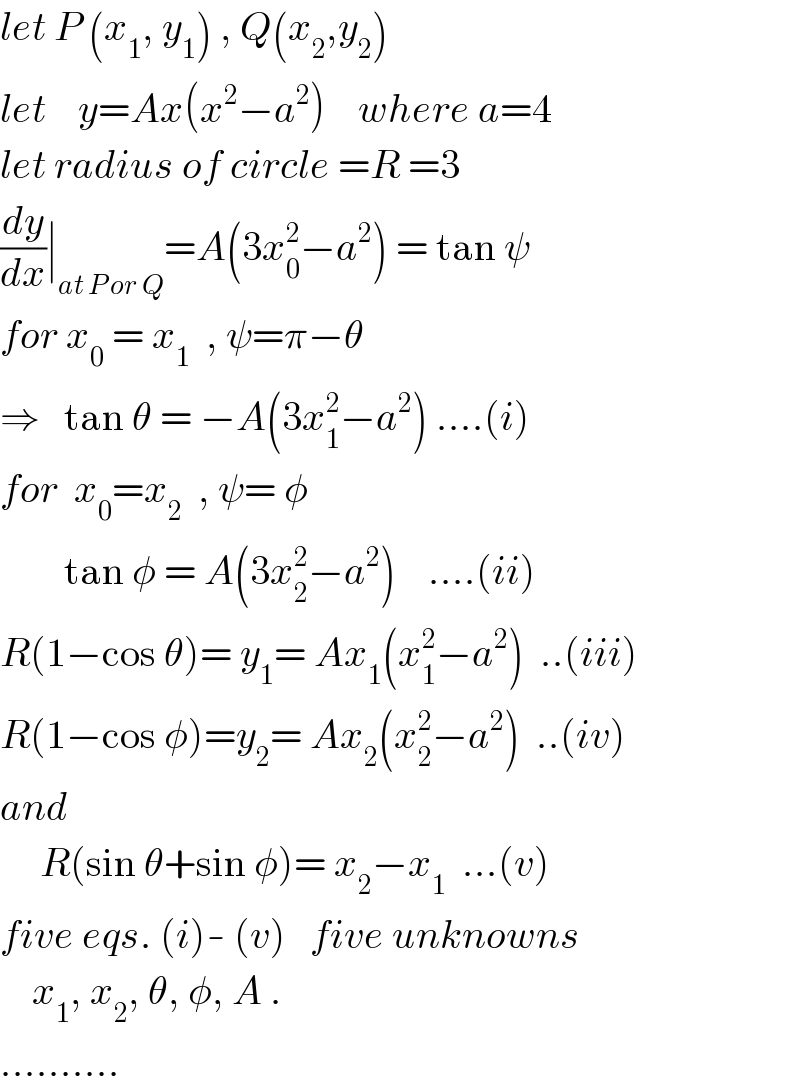
$${let}\:{P}\:\left({x}_{\mathrm{1}} ,\:{y}_{\mathrm{1}} \right)\:,\:{Q}\left({x}_{\mathrm{2}} ,{y}_{\mathrm{2}} \right) \\ $$$${let}\:\:\:\:{y}={Ax}\left({x}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)\:\:\:\:{where}\:{a}=\mathrm{4} \\ $$$${let}\:{radius}\:{of}\:{circle}\:={R}\:=\mathrm{3} \\ $$$$\frac{{dy}}{{dx}}\mid_{{at}\:{P}\:{or}\:{Q}} ={A}\left(\mathrm{3}{x}_{\mathrm{0}} ^{\mathrm{2}} −{a}^{\mathrm{2}} \right)\:=\:\mathrm{tan}\:\psi \\ $$$${for}\:{x}_{\mathrm{0}} \:=\:{x}_{\mathrm{1}} \:\:,\:\psi=\pi−\theta \\ $$$$\Rightarrow\:\:\:\mathrm{tan}\:\theta\:=\:−{A}\left(\mathrm{3}{x}_{\mathrm{1}} ^{\mathrm{2}} −{a}^{\mathrm{2}} \right)\:….\left({i}\right) \\ $$$${for}\:\:{x}_{\mathrm{0}} ={x}_{\mathrm{2}} \:\:,\:\psi=\:\phi \\ $$$$\:\:\:\:\:\:\:\:\mathrm{tan}\:\phi\:=\:{A}\left(\mathrm{3}{x}_{\mathrm{2}} ^{\mathrm{2}} −{a}^{\mathrm{2}} \right)\:\:\:\:….\left({ii}\right) \\ $$$${R}\left(\mathrm{1}−\mathrm{cos}\:\theta\right)=\:{y}_{\mathrm{1}} =\:{Ax}_{\mathrm{1}} \left({x}_{\mathrm{1}} ^{\mathrm{2}} −{a}^{\mathrm{2}} \right)\:\:..\left({iii}\right) \\ $$$${R}\left(\mathrm{1}−\mathrm{cos}\:\phi\right)={y}_{\mathrm{2}} =\:{Ax}_{\mathrm{2}} \left({x}_{\mathrm{2}} ^{\mathrm{2}} −{a}^{\mathrm{2}} \right)\:\:..\left({iv}\right) \\ $$$${and} \\ $$$$\:\:\:\:\:{R}\left(\mathrm{sin}\:\theta+\mathrm{sin}\:\phi\right)=\:{x}_{\mathrm{2}} −{x}_{\mathrm{1}} \:\:…\left({v}\right) \\ $$$${five}\:{eqs}.\:\left({i}\right)-\:\left({v}\right)\:\:\:{five}\:{unknowns} \\ $$$$\:\:\:\:{x}_{\mathrm{1}} ,\:{x}_{\mathrm{2}} ,\:\theta,\:\phi,\:{A}\:. \\ $$$$………. \\ $$
Answered by MrW3 last updated on 01/Oct/18
![eqn. of cubic: y=ax(x−4)(x+4)=a(x^3 −16x) y′=a(3x^2 −16) eqn. of circle: (x−b)^2 +(y−3)^2 =3^2 2(x−b)+2(y−3)y′=0 y′=−((x−b)/(y−3)) let touching point be P(u,v) v=au(u^2 −16) (u−b)^2 +(v−3)^2 =3^2 a(3u^2 −16)=−((u−b)/(v−3)) u−b=−(v−3)a(3u^2 −16) (v−3)^2 [a^2 (3u^2 −16)^2 +1]=3^2 ⇒[au(u^2 −16)−3]^2 [a^2 (3u^2 −16)^2 +1]=3^2 ....](https://www.tinkutara.com/question/Q44595.png)
$${eqn}.\:{of}\:{cubic}: \\ $$$${y}={ax}\left({x}−\mathrm{4}\right)\left({x}+\mathrm{4}\right)={a}\left({x}^{\mathrm{3}} −\mathrm{16}{x}\right) \\ $$$${y}'={a}\left(\mathrm{3}{x}^{\mathrm{2}} −\mathrm{16}\right) \\ $$$$ \\ $$$${eqn}.\:{of}\:{circle}: \\ $$$$\left({x}−{b}\right)^{\mathrm{2}} +\left({y}−\mathrm{3}\right)^{\mathrm{2}} =\mathrm{3}^{\mathrm{2}} \\ $$$$\mathrm{2}\left({x}−{b}\right)+\mathrm{2}\left({y}−\mathrm{3}\right){y}'=\mathrm{0} \\ $$$${y}'=−\frac{{x}−{b}}{{y}−\mathrm{3}} \\ $$$$ \\ $$$${let}\:{touching}\:{point}\:{be}\:{P}\left({u},{v}\right) \\ $$$${v}={au}\left({u}^{\mathrm{2}} −\mathrm{16}\right) \\ $$$$\left({u}−{b}\right)^{\mathrm{2}} +\left({v}−\mathrm{3}\right)^{\mathrm{2}} =\mathrm{3}^{\mathrm{2}} \\ $$$${a}\left(\mathrm{3}{u}^{\mathrm{2}} −\mathrm{16}\right)=−\frac{{u}−{b}}{{v}−\mathrm{3}} \\ $$$${u}−{b}=−\left({v}−\mathrm{3}\right){a}\left(\mathrm{3}{u}^{\mathrm{2}} −\mathrm{16}\right) \\ $$$$\left({v}−\mathrm{3}\right)^{\mathrm{2}} \left[{a}^{\mathrm{2}} \left(\mathrm{3}{u}^{\mathrm{2}} −\mathrm{16}\right)^{\mathrm{2}} +\mathrm{1}\right]=\mathrm{3}^{\mathrm{2}} \\ $$$$\Rightarrow\left[{au}\left({u}^{\mathrm{2}} −\mathrm{16}\right)−\mathrm{3}\right]^{\mathrm{2}} \left[{a}^{\mathrm{2}} \left(\mathrm{3}{u}^{\mathrm{2}} −\mathrm{16}\right)^{\mathrm{2}} +\mathrm{1}\right]=\mathrm{3}^{\mathrm{2}} \\ $$$$…. \\ $$
Commented by MrW3 last updated on 02/Oct/18

$${my}\:{intention}\:{was}\:{which}\:{value}\:{a}\:{should} \\ $$$${have}\:{such}\:{that}\:{the}\:{last}\:{eqn}.\:{has}\:{only} \\ $$$${two}\:{suitable}\:{solutions}\:{for}\:{u}. \\ $$
Commented by ajfour last updated on 02/Oct/18
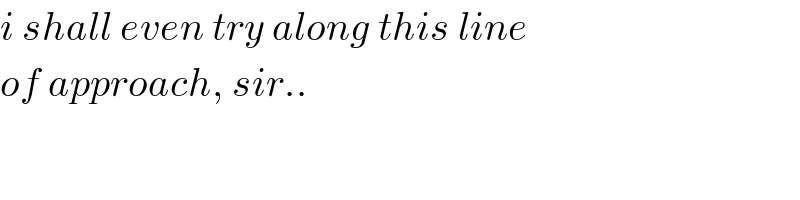
$${i}\:{shall}\:{even}\:{try}\:{along}\:{this}\:{line} \\ $$$${of}\:{approach},\:{sir}.. \\ $$
