Menu Close

Question-44573

Tinku Tara 0 Comments
Pin




Question Number 44573 by Raj Singh last updated on 01/Oct/18
Commented by maxmathsup by imad last updated on 01/Oct/18
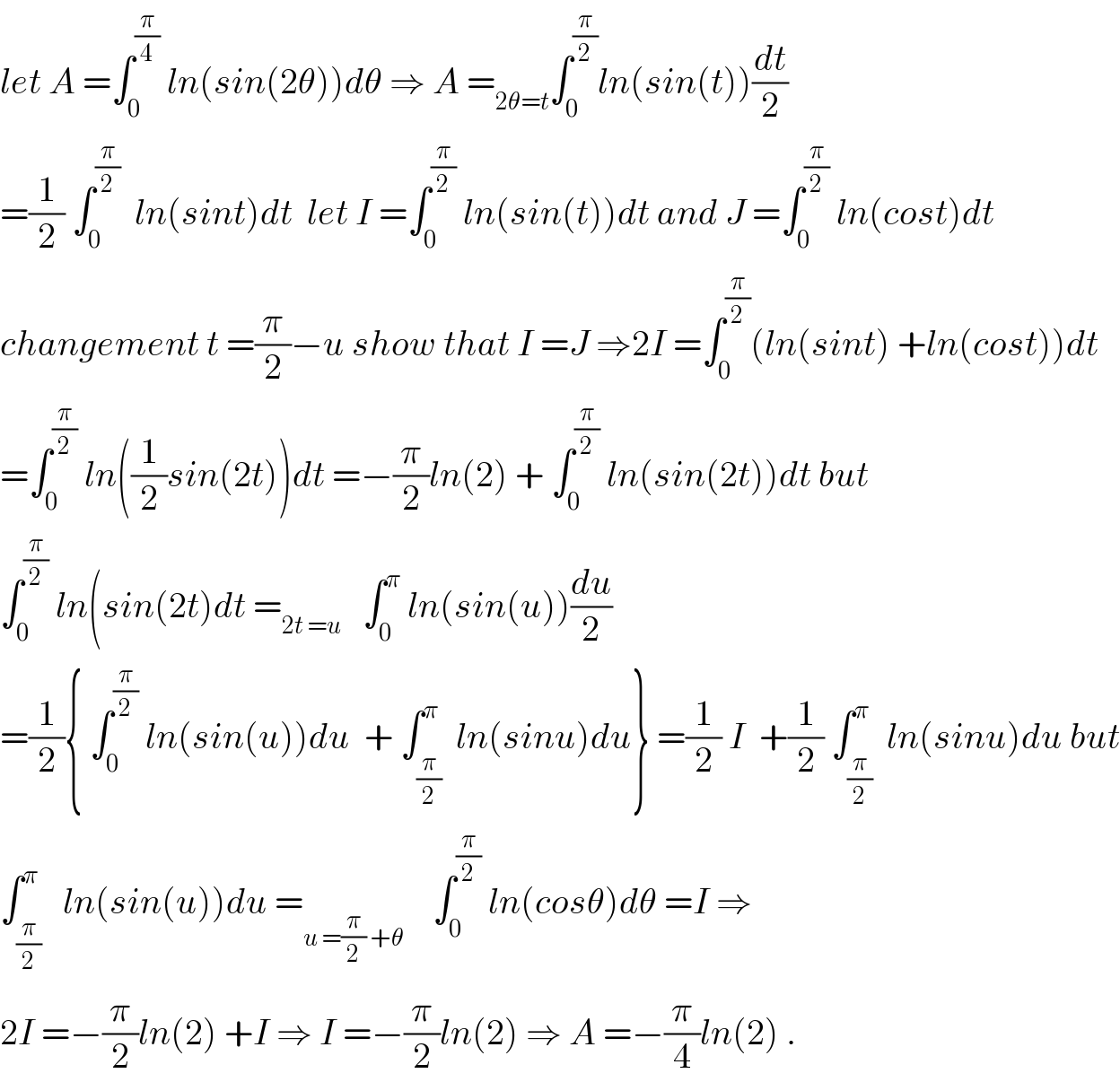
let A =∫_0 ^(π/4) ln(sin(2θ))dθ ⇒ A =_(2θ=t) ∫_0 ^(π/2) ln(sin(t))(dt/2) =(1/2) ∫_0 ^(π/2) ln(sint)dt let I =∫_0 ^(π/2) ln(sin(t))dt and J =∫_0 ^(π/2) ln(cost)dt changement t =(π/2)−u show that I =J ⇒2I =∫_0 ^(π/2) (ln(sint) +ln(cost))dt =∫_0 ^(π/2) ln((1/2)sin(2t))dt =−(π/2)ln(2) + ∫_0 ^(π/2) ln(sin(2t))dt but ∫_0 ^(π/2) ln(sin(2t)dt =_(2t =u) ∫_0 ^π ln(sin(u))(du/2) =(1/2){ ∫_0 ^(π/2) ln(sin(u))du + ∫_(π/2) ^π ln(sinu)du} =(1/2) I +(1/2) ∫_(π/2) ^π ln(sinu)du but ∫_(π/2) ^π ln(sin(u))du =_(u =(π/2) +θ) ∫_0 ^(π/2) ln(cosθ)dθ =I ⇒ 2I =−(π/2)ln(2) +I ⇒ I =−(π/2)ln(2) ⇒ A =−(π/4)ln(2) .
$${let}\:{A}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{ln}\left({sin}\left(\mathrm{2}\theta\right)\right){d}\theta\:\Rightarrow\:{A}\:=_{\mathrm{2}\theta={t}} \int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({sin}\left({t}\right)\right)\frac{{dt}}{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:{ln}\left({sint}\right){dt}\:\:{let}\:{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{ln}\left({sin}\left({t}\right)\right){dt}\:{and}\:{J}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{ln}\left({cost}\right){dt} \\ $$$${changement}\:{t}\:=\frac{\pi}{\mathrm{2}}−{u}\:{show}\:{that}\:{I}\:={J}\:\Rightarrow\mathrm{2}{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left({ln}\left({sint}\right)\:+{ln}\left({cost}\right)\right){dt} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{ln}\left(\frac{\mathrm{1}}{\mathrm{2}}{sin}\left(\mathrm{2}{t}\right)\right){dt}\:=−\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{2}\right)\:+\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{ln}\left({sin}\left(\mathrm{2}{t}\right)\right){dt}\:{but} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{ln}\left({sin}\left(\mathrm{2}{t}\right){dt}\:=_{\mathrm{2}{t}\:={u}} \:\:\:\int_{\mathrm{0}} ^{\pi} \:{ln}\left({sin}\left({u}\right)\right)\frac{{du}}{\mathrm{2}}\right. \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{ln}\left({sin}\left({u}\right)\right){du}\:\:+\:\int_{\frac{\pi}{\mathrm{2}}} ^{\pi} \:{ln}\left({sinu}\right){du}\right\}\:=\frac{\mathrm{1}}{\mathrm{2}}\:{I}\:\:+\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\frac{\pi}{\mathrm{2}}} ^{\pi} \:{ln}\left({sinu}\right){du}\:{but} \\ $$$$\int_{\frac{\pi}{\mathrm{2}}} ^{\pi} \:\:{ln}\left({sin}\left({u}\right)\right){du}\:=_{{u}\:=\frac{\pi}{\mathrm{2}}\:+\theta} \:\:\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{ln}\left({cos}\theta\right){d}\theta\:={I}\:\Rightarrow \\ $$$$\mathrm{2}{I}\:=−\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{2}\right)\:+{I}\:\Rightarrow\:{I}\:=−\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{2}\right)\:\Rightarrow\:{A}\:=−\frac{\pi}{\mathrm{4}}{ln}\left(\mathrm{2}\right)\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 01/Oct/18
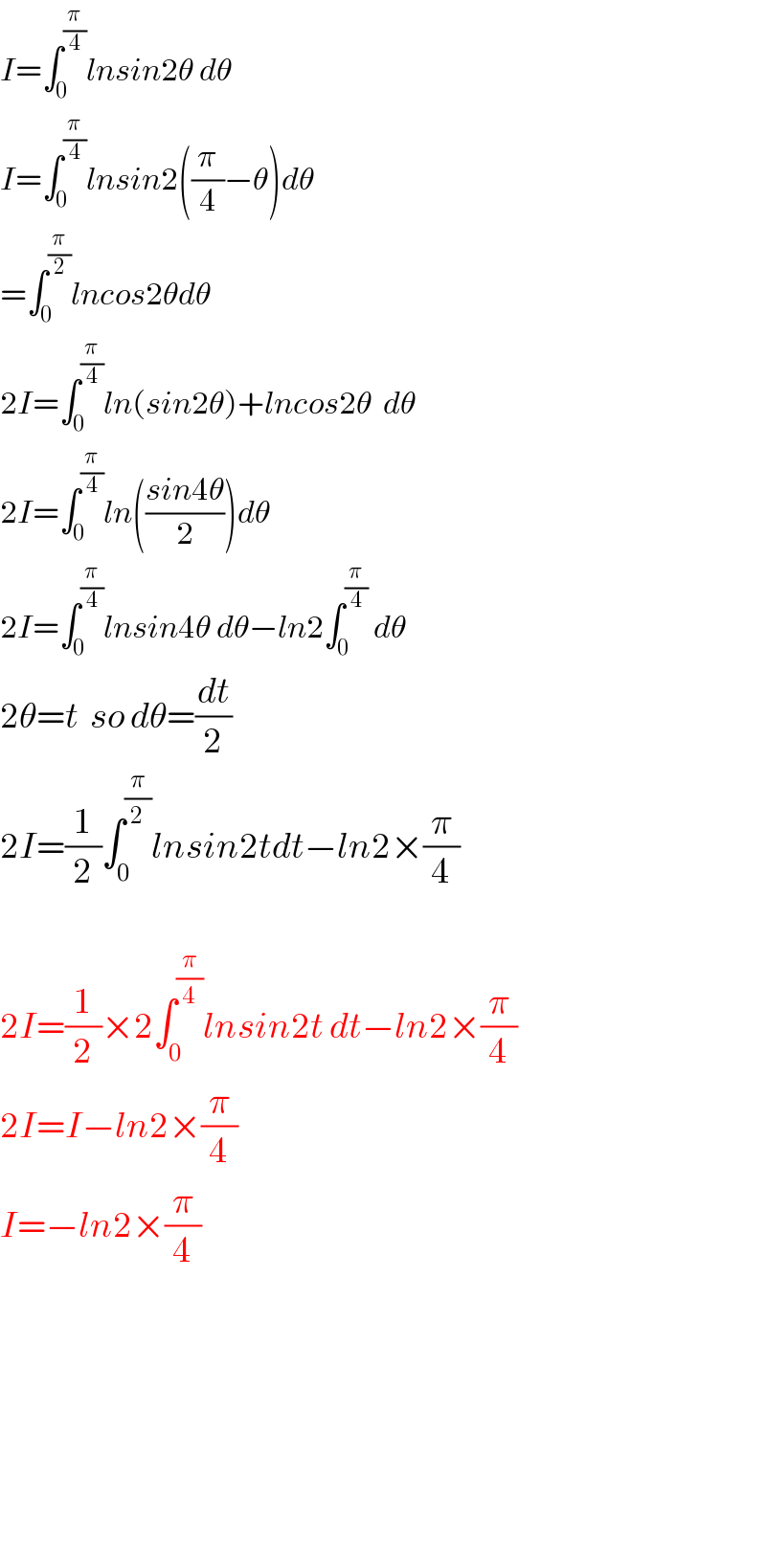
I=∫_0 ^(π/4) lnsin2θ dθ I=∫_0 ^(π/4) lnsin2((π/4)−θ)dθ =∫_0 ^(π/2) lncos2θdθ 2I=∫_0 ^(π/4) ln(sin2θ)+lncos2θ dθ 2I=∫_0 ^(π/4) ln(((sin4θ)/2))dθ 2I=∫_0 ^(π/4) lnsin4θ dθ−ln2∫_0 ^(π/4) dθ 2θ=t so dθ=(dt/2) 2I=(1/2)∫_0 ^(π/2) lnsin2tdt−ln2×(π/4) 2I=(1/2)×2∫_0 ^(π/4) lnsin2t dt−ln2×(π/4) 2I=I−ln2×(π/4) I=−ln2×(π/4)
$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {lnsin}\mathrm{2}\theta\:{d}\theta \\ $$$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {lnsin}\mathrm{2}\left(\frac{\pi}{\mathrm{4}}−\theta\right){d}\theta \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {lncos}\mathrm{2}\theta{d}\theta \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({sin}\mathrm{2}\theta\right)+{lncos}\mathrm{2}\theta\:\:{d}\theta \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\frac{{sin}\mathrm{4}\theta}{\mathrm{2}}\right){d}\theta \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {lnsin}\mathrm{4}\theta\:{d}\theta−{ln}\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{d}\theta \\ $$$$\mathrm{2}\theta={t}\:\:{so}\:{d}\theta=\frac{{dt}}{\mathrm{2}} \\ $$$$\mathrm{2}{I}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {lnsin}\mathrm{2}{tdt}−{ln}\mathrm{2}×\frac{\pi}{\mathrm{4}} \\ $$$$ \\ $$$$\mathrm{2}{I}=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {lnsin}\mathrm{2}{t}\:{dt}−{ln}\mathrm{2}×\frac{\pi}{\mathrm{4}} \\ $$$$\mathrm{2}{I}={I}−{ln}\mathrm{2}×\frac{\pi}{\mathrm{4}} \\ $$$${I}=−{ln}\mathrm{2}×\frac{\pi}{\mathrm{4}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *