Question Number 44729 by behi83417@gmail.com last updated on 03/Oct/18
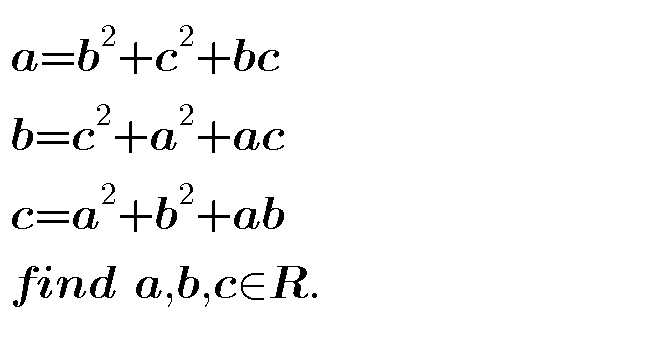
Answered by MJS last updated on 04/Oct/18

$$\mathrm{trivial}\:\mathrm{solutions}\:{a}={b}={c}=\mathrm{0}\:\vee\:{a}={b}={c}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$ \\ $$$${c}^{\mathrm{2}} +{bc}+{b}^{\mathrm{2}} −{a}=\mathrm{0} \\ $$$${c}^{\mathrm{2}} +{ac}+{a}^{\mathrm{2}} −{b}=\mathrm{0} \\ $$$$\left({b}−{a}\right){c}+{b}^{\mathrm{2}} −{a}^{\mathrm{2}} +{b}−{a}=\mathrm{0} \\ $$$${c}=−\left({a}+{b}+\mathrm{1}\right) \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{ab}+{a}+{b}+\mathrm{1}=\mathrm{0} \\ $$$${b}^{\mathrm{2}} +\left({a}+\mathrm{1}\right){b}+{a}^{\mathrm{2}} +{a}+\mathrm{1}=\mathrm{0} \\ $$$${b}=−\frac{{a}+\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{−\mathrm{3}{a}^{\mathrm{2}} −\mathrm{2}{a}−\mathrm{3}}}{\mathrm{2}} \\ $$$${c}=−\frac{{a}+\mathrm{1}}{\mathrm{2}}\mp\frac{\sqrt{−\mathrm{3}{a}^{\mathrm{2}} −\mathrm{2}{a}−\mathrm{3}}}{\mathrm{2}} \\ $$$${a}={b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{bc}\:\mathrm{always}\:\mathrm{true} \\ $$$${a}\in\mathbb{R}\:\Rightarrow\:{b},\:{c}\notin\mathbb{R} \\ $$
Answered by ajfour last updated on 04/Oct/18
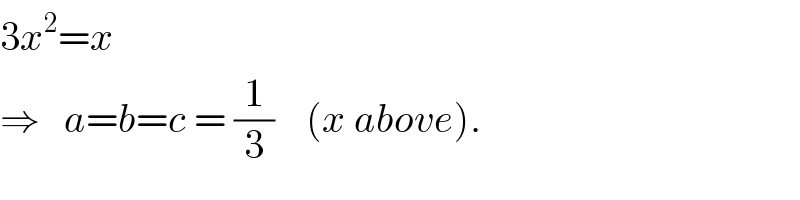
$$\mathrm{3}{x}^{\mathrm{2}} ={x} \\ $$$$\Rightarrow\:\:\:{a}={b}={c}\:=\:\frac{\mathrm{1}}{\mathrm{3}}\:\:\:\:\left({x}\:{above}\right). \\ $$
Answered by ajfour last updated on 04/Oct/18
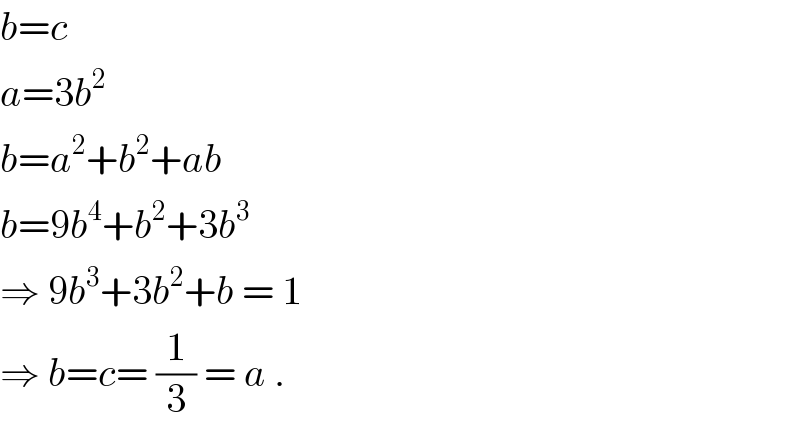
$${b}={c} \\ $$$${a}=\mathrm{3}{b}^{\mathrm{2}} \\ $$$${b}={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{ab} \\ $$$${b}=\mathrm{9}{b}^{\mathrm{4}} +{b}^{\mathrm{2}} +\mathrm{3}{b}^{\mathrm{3}} \\ $$$$\Rightarrow\:\mathrm{9}{b}^{\mathrm{3}} +\mathrm{3}{b}^{\mathrm{2}} +{b}\:=\:\mathrm{1} \\ $$$$\Rightarrow\:{b}={c}=\:\frac{\mathrm{1}}{\mathrm{3}}\:=\:{a}\:. \\ $$
Commented by behi83417@gmail.com last updated on 04/Oct/18
$${thank}\:{you}\:{very}\:{much}\:{dear}\:{my} \\ $$$${friends}. \\ $$$$….{also}\:{waiting}\:{for}\:{mrW}\mathrm{3}'{s}\:{proof}. \\ $$
Answered by MrW3 last updated on 04/Oct/18
![(i)−(ii): a−b=b^2 −a^2 +bc−ac (b+a)(b−a)+(b−a)c+(b−a)=0 ⇒(a+b+c+1)(b−a)=0 similarly ⇒(a+b+c+1)(c−b)=0 ⇒(a+b+c+1)(a−c)=0 case 1: a=b=c=k ⇒k=3k^2 ⇒k=0 or k=(1/3) case 2: a+b+c+1=0 a=(b+c)^2 −bc ...(1) b=(c+a)^2 −ca ...(2) c=(a+b)^2 −ab ...(3) a=(1+a)^2 −bc b=(a+c)^2 −ca c=(1+c)^2 −ab a=(1+a)^2 −c[(a+c)^2 −ca] a=(1+a)^2 −c(a+c)^2 +c^2 a a^2 =a(1+a)^2 −ac(a+c)^2 +c^2 a^2 c=(1+c)^2 −a[(a+c)^2 −ca] c=(1+c)^2 −a(a+c)^2 +a^2 c c^2 =c(1+c)^2 −ac(a+c)^2 +a^2 c^2 a^2 −c^2 =a(1+a)^2 −c(1+c)^2 a^2 −c^2 =a+2a^2 +a^3 −c−2c^2 −c^3 a+a^2 +a^3 =c+c^2 +c^3 =h say similarly a+a^2 +a^3 =b+b^2 +b^3 =h since x+x^2 +x^3 =h has only one single real solution, lets say x=p, we get a=b=c=x=p i.e. case 2 gives the same solution as case 1.](https://www.tinkutara.com/question/Q44758.png)
$$\left({i}\right)−\left({ii}\right): \\ $$$${a}−{b}={b}^{\mathrm{2}} −{a}^{\mathrm{2}} +{bc}−{ac} \\ $$$$\left({b}+{a}\right)\left({b}−{a}\right)+\left({b}−{a}\right){c}+\left({b}−{a}\right)=\mathrm{0} \\ $$$$\Rightarrow\left({a}+{b}+{c}+\mathrm{1}\right)\left({b}−{a}\right)=\mathrm{0} \\ $$$${similarly} \\ $$$$\Rightarrow\left({a}+{b}+{c}+\mathrm{1}\right)\left({c}−{b}\right)=\mathrm{0} \\ $$$$\Rightarrow\left({a}+{b}+{c}+\mathrm{1}\right)\left({a}−{c}\right)=\mathrm{0} \\ $$$$ \\ $$$${case}\:\mathrm{1}:\:{a}={b}={c}={k} \\ $$$$\Rightarrow{k}=\mathrm{3}{k}^{\mathrm{2}} \\ $$$$\Rightarrow{k}=\mathrm{0}\:{or}\:{k}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$ \\ $$$${case}\:\mathrm{2}:\:{a}+{b}+{c}+\mathrm{1}=\mathrm{0} \\ $$$${a}=\left({b}+{c}\right)^{\mathrm{2}} −{bc}\:\:\:\:…\left(\mathrm{1}\right) \\ $$$${b}=\left({c}+{a}\right)^{\mathrm{2}} −{ca}\:\:\:\:…\left(\mathrm{2}\right) \\ $$$${c}=\left({a}+{b}\right)^{\mathrm{2}} −{ab}\:\:\:\:…\left(\mathrm{3}\right) \\ $$$$ \\ $$$${a}=\left(\mathrm{1}+{a}\right)^{\mathrm{2}} −{bc} \\ $$$${b}=\left({a}+{c}\right)^{\mathrm{2}} −{ca} \\ $$$${c}=\left(\mathrm{1}+{c}\right)^{\mathrm{2}} −{ab} \\ $$$$ \\ $$$${a}=\left(\mathrm{1}+{a}\right)^{\mathrm{2}} −{c}\left[\left({a}+{c}\right)^{\mathrm{2}} −{ca}\right] \\ $$$${a}=\left(\mathrm{1}+{a}\right)^{\mathrm{2}} −{c}\left({a}+{c}\right)^{\mathrm{2}} +{c}^{\mathrm{2}} {a} \\ $$$${a}^{\mathrm{2}} ={a}\left(\mathrm{1}+{a}\right)^{\mathrm{2}} −{ac}\left({a}+{c}\right)^{\mathrm{2}} +{c}^{\mathrm{2}} {a}^{\mathrm{2}} \\ $$$${c}=\left(\mathrm{1}+{c}\right)^{\mathrm{2}} −{a}\left[\left({a}+{c}\right)^{\mathrm{2}} −{ca}\right] \\ $$$${c}=\left(\mathrm{1}+{c}\right)^{\mathrm{2}} −{a}\left({a}+{c}\right)^{\mathrm{2}} +{a}^{\mathrm{2}} {c} \\ $$$${c}^{\mathrm{2}} ={c}\left(\mathrm{1}+{c}\right)^{\mathrm{2}} −{ac}\left({a}+{c}\right)^{\mathrm{2}} +{a}^{\mathrm{2}} {c}^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} −{c}^{\mathrm{2}} ={a}\left(\mathrm{1}+{a}\right)^{\mathrm{2}} −{c}\left(\mathrm{1}+{c}\right)^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} −{c}^{\mathrm{2}} ={a}+\mathrm{2}{a}^{\mathrm{2}} +{a}^{\mathrm{3}} −{c}−\mathrm{2}{c}^{\mathrm{2}} −{c}^{\mathrm{3}} \\ $$$${a}+{a}^{\mathrm{2}} +{a}^{\mathrm{3}} ={c}+{c}^{\mathrm{2}} +{c}^{\mathrm{3}} ={h}\:{say} \\ $$$${similarly} \\ $$$${a}+{a}^{\mathrm{2}} +{a}^{\mathrm{3}} ={b}+{b}^{\mathrm{2}} +{b}^{\mathrm{3}} ={h} \\ $$$${since}\:{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} ={h}\:{has}\:{only}\:{one}\:{single} \\ $$$${real}\:{solution},\:{lets}\:{say}\:{x}={p}, \\ $$$${we}\:{get}\:{a}={b}={c}={x}={p} \\ $$$${i}.{e}.\:{case}\:\mathrm{2}\:{gives}\:{the}\:{same}\:{solution}\:{as} \\ $$$${case}\:\mathrm{1}. \\ $$
Commented by behi83417@gmail.com last updated on 04/Oct/18
$${perfect}!\:{thank}\:{you}\:{dear}\:{master}. \\ $$
