Question Number 44749 by ajfour last updated on 04/Oct/18
Commented by ajfour last updated on 04/Oct/18
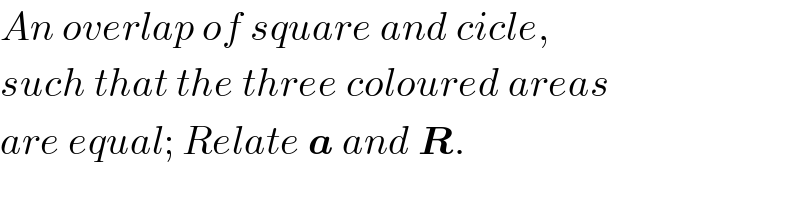
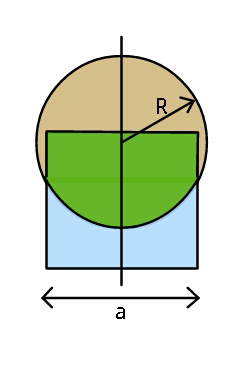
$${An}\:{overlap}\:{of}\:{square}\:{and}\:{cicle}, \\ $$$${such}\:{that}\:{the}\:{three}\:{coloured}\:{areas} \\ $$$${are}\:{equal};\:{Relate}\:\boldsymbol{{a}}\:{and}\:\boldsymbol{{R}}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 04/Oct/18
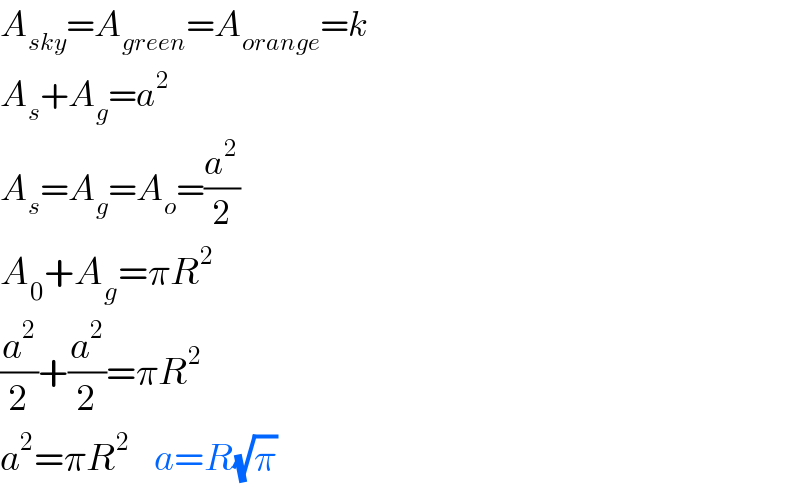
$${A}_{{sky}} ={A}_{{green}} ={A}_{{orange}} ={k} \\ $$$${A}_{{s}} +{A}_{{g}} ={a}^{\mathrm{2}} \: \\ $$$${A}_{{s}} ={A}_{{g}} ={A}_{{o}} =\frac{{a}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${A}_{\mathrm{0}} +{A}_{{g}} =\pi{R}^{\mathrm{2}} \\ $$$$\frac{{a}^{\mathrm{2}} }{\mathrm{2}}+\frac{{a}^{\mathrm{2}} }{\mathrm{2}}=\pi{R}^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} =\pi{R}^{\mathrm{2}} \:\:\:\:{a}={R}\sqrt{\pi}\: \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 04/Oct/18

$${your}\:{all}\:{problems}\:{are}\:{mindblowing}..{thank}\:{you}.. \\ $$
Commented by ajfour last updated on 04/Oct/18
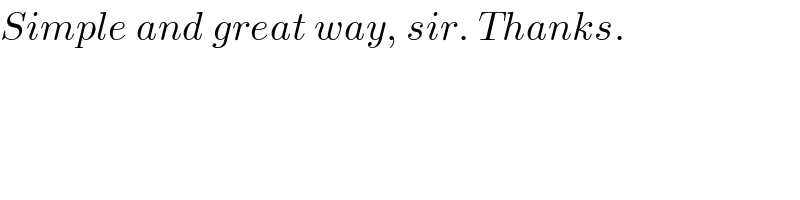
$${Simple}\:{and}\:{great}\:{way},\:{sir}.\:{Thanks}. \\ $$
