Question Number 44801 by ajfour last updated on 04/Oct/18
Commented by ajfour last updated on 04/Oct/18
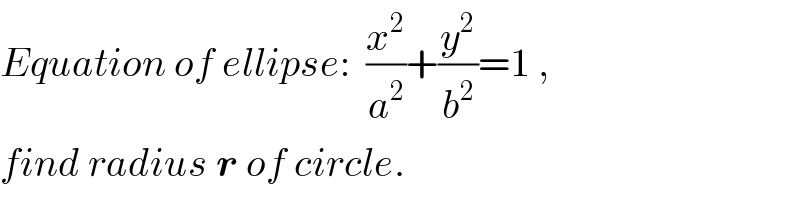
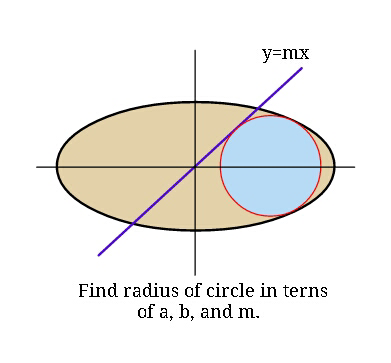
$${Equation}\:{of}\:{ellipse}:\:\:\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1}\:, \\ $$$${find}\:{radius}\:\boldsymbol{{r}}\:{of}\:{circle}. \\ $$
Answered by ajfour last updated on 05/Oct/18
![let centre of circle be (h,0) h = (r/(sin tan^(−1) m)) = ((r(√(1+m^2 )))/m) point of contact (upper) : (x_0 ,y_0 ) { ((x_0 =acos φ = h+rcos θ )),((y_0 = bsin φ = rsin θ)) :} tan φ = ((arsin θ)/(b(h+rcos θ))) ....(i) (dy/dx)∣_x_0 = ((bcos φ)/(−asin φ)) = −((cos θ)/(sin θ)) ⇒ tan φ = ((bsin θ)/(acos θ)) ...(ii) comparing (i)&(ii) ((arsin θ)/(b(h+rcos θ))) = ((bsin θ)/(acos θ)) as θ≠0 , a^2 rcos θ = b^2 h+b^2 rcos θ ________________________ { ((if θ = 0 ⇒ a = b, then)),(( r = a−h = a−((r(√(1+m^2 )))/m))) :} ⇒ r = (a/(1+((√(1+m^2 ))/m))) ________________________ But when its not so ⇒ cos θ = ((b^2 h)/(r(a^2 −b^2 ))) from first bracket eqs. (((h+rcos θ)^2 )/a^2 ) +(((rsin θ)^2 )/b^2 ) = 1 ⇒ b^2 (h+rcos θ)^2 +a^2 (r^2 −r^2 cos^2 θ) = a^2 b^2 b^2 (h+((b^2 h)/(a^2 −b^2 )))^2 +a^2 [r^2 −(((b^2 h)/(a^2 −b^2 )))^2 ] = a^2 b^2 ⇒ r^2 = ((b^4 h^2 )/((a^2 −b^2 )^2 ))+b^2 −((a^2 b^2 h^2 )/((a^2 −b^2 )^2 )) r^2 = b^2 (1−(h^2 /(a^2 −b^2 ))) but h^2 = r^2 +(r^2 /m^2 ) ⇒ r^2 = b^2 −((b^2 r^2 )/(a^2 −b^2 ))−((b^2 r^2 )/(m^2 (a^2 −b^2 ))) r^2 [1+((b^2 /(a^2 −b^2 )))(1+(1/m^2 ))]= b^2 ________________________ r = (b/( (√(1+((b^2 /(a^2 −b^2 )))(1+(1/m^2 )))))) If θ ≠ 0 (same as a ≠ b).](https://www.tinkutara.com/question/Q44868.png)
$${let}\:{centre}\:{of}\:{circle}\:{be}\:\left({h},\mathrm{0}\right) \\ $$$$\:\:\:\boldsymbol{{h}}\:=\:\frac{\boldsymbol{{r}}}{\mathrm{sin}\:\mathrm{tan}^{−\mathrm{1}} \boldsymbol{{m}}}\:=\:\frac{{r}\sqrt{\mathrm{1}+{m}^{\mathrm{2}} }}{{m}} \\ $$$$\:\:{point}\:{of}\:{contact}\:\left({upper}\right)\::\:\left({x}_{\mathrm{0}} ,{y}_{\mathrm{0}} \right) \\ $$$$\:\:\:\begin{cases}{{x}_{\mathrm{0}} ={a}\mathrm{cos}\:\phi\:=\:{h}+{r}\mathrm{cos}\:\theta\:}\\{{y}_{\mathrm{0}} =\:{b}\mathrm{sin}\:\phi\:=\:{r}\mathrm{sin}\:\theta}\end{cases} \\ $$$$\:\:\:\:\:\:\mathrm{tan}\:\phi\:=\:\frac{{ar}\mathrm{sin}\:\theta}{{b}\left({h}+{r}\mathrm{cos}\:\theta\right)}\:\:\:….\left({i}\right) \\ $$$$\:\:\:\frac{{dy}}{{dx}}\mid_{{x}_{\mathrm{0}} } =\:\frac{{b}\mathrm{cos}\:\phi}{−{a}\mathrm{sin}\:\phi}\:=\:−\frac{\mathrm{cos}\:\theta}{\mathrm{sin}\:\theta} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\:\mathrm{tan}\:\phi\:=\:\frac{{b}\mathrm{sin}\:\theta}{{a}\mathrm{cos}\:\theta}\:\:\:…\left({ii}\right) \\ $$$${comparing}\:\left({i}\right)\&\left({ii}\right) \\ $$$$\:\:\:\:\:\:\:\frac{{ar}\mathrm{sin}\:\theta}{{b}\left({h}+{r}\mathrm{cos}\:\theta\right)}\:=\:\frac{{b}\mathrm{sin}\:\theta}{{a}\mathrm{cos}\:\theta} \\ $$$${as}\:\theta\neq\mathrm{0}\:,\:\:{a}^{\mathrm{2}} {r}\mathrm{cos}\:\theta\:=\:{b}^{\mathrm{2}} {h}+{b}^{\mathrm{2}} {r}\mathrm{cos}\:\theta \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\:\begin{cases}{{if}\:\:\theta\:=\:\mathrm{0}\:\Rightarrow\:\:\boldsymbol{{a}}\:=\:\boldsymbol{{b}},\:{then}}\\{\:\:\boldsymbol{{r}}\:=\:\boldsymbol{{a}}−\boldsymbol{{h}}\:=\:\boldsymbol{{a}}−\frac{\boldsymbol{{r}}\sqrt{\mathrm{1}+\boldsymbol{{m}}^{\mathrm{2}} }}{\boldsymbol{{m}}}}\end{cases} \\ $$$$\Rightarrow\:\:\:{r}\:=\:\frac{{a}}{\mathrm{1}+\frac{\sqrt{\mathrm{1}+{m}^{\mathrm{2}} }}{{m}}}\:\: \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\:\:{But}\:{when}\:{its}\:{not}\:{so} \\ $$$$\Rightarrow\:\:\:\:\:\:\mathrm{cos}\:\theta\:=\:\frac{{b}^{\mathrm{2}} {h}}{{r}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)} \\ $$$${from}\:{first}\:{bracket}\:{eqs}. \\ $$$$\:\:\:\:\:\:\frac{\left({h}+{r}\mathrm{cos}\:\theta\right)^{\mathrm{2}} }{{a}^{\mathrm{2}} }\:+\frac{\left({r}\mathrm{sin}\:\theta\right)^{\mathrm{2}} }{{b}^{\mathrm{2}} }\:=\:\mathrm{1} \\ $$$$\Rightarrow\:\:{b}^{\mathrm{2}} \left({h}+{r}\mathrm{cos}\:\theta\right)^{\mathrm{2}} +{a}^{\mathrm{2}} \left({r}^{\mathrm{2}} −{r}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:{a}^{\mathrm{2}} {b}^{\mathrm{2}} \\ $$$${b}^{\mathrm{2}} \left({h}+\frac{{b}^{\mathrm{2}} {h}}{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }\right)^{\mathrm{2}} +{a}^{\mathrm{2}} \left[{r}^{\mathrm{2}} −\left(\frac{{b}^{\mathrm{2}} {h}}{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }\right)^{\mathrm{2}} \right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:{a}^{\mathrm{2}} {b}^{\mathrm{2}} \\ $$$$\Rightarrow\:{r}^{\mathrm{2}} \:=\:\frac{{b}^{\mathrm{4}} {h}^{\mathrm{2}} }{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} }+{b}^{\mathrm{2}} −\frac{{a}^{\mathrm{2}} {b}^{\mathrm{2}} {h}^{\mathrm{2}} }{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\boldsymbol{{r}}^{\mathrm{2}} \:=\:\boldsymbol{{b}}^{\mathrm{2}} \left(\mathrm{1}−\frac{\boldsymbol{{h}}^{\mathrm{2}} }{\boldsymbol{{a}}^{\mathrm{2}} −\boldsymbol{{b}}^{\mathrm{2}} }\right) \\ $$$${but}\:\:\:{h}^{\mathrm{2}} \:=\:{r}^{\mathrm{2}} +\frac{{r}^{\mathrm{2}} }{{m}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\:{r}^{\mathrm{2}} \:=\:{b}^{\mathrm{2}} −\frac{{b}^{\mathrm{2}} {r}^{\mathrm{2}} }{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }−\frac{{b}^{\mathrm{2}} {r}^{\mathrm{2}} }{{m}^{\mathrm{2}} \left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)} \\ $$$$\:{r}^{\mathrm{2}} \left[\mathrm{1}+\left(\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }\right)\left(\mathrm{1}+\frac{\mathrm{1}}{{m}^{\mathrm{2}} }\right)\right]=\:{b}^{\mathrm{2}} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\:\:\:\:\boldsymbol{{r}}\:=\:\frac{\boldsymbol{{b}}}{\:\sqrt{\mathrm{1}+\left(\frac{\boldsymbol{{b}}^{\mathrm{2}} }{\boldsymbol{{a}}^{\mathrm{2}} −\boldsymbol{{b}}^{\mathrm{2}} }\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\boldsymbol{{m}}^{\mathrm{2}} }\right)}}\: \\ $$$$\:\:\:\:\:\:\:{If}\:\theta\:\neq\:\mathrm{0}\:\:\left({same}\:{as}\:{a}\:\neq\:{b}\right). \\ $$
Commented by ajfour last updated on 05/Oct/18
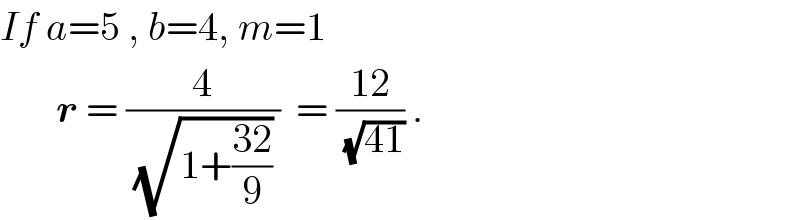
$${If}\:{a}=\mathrm{5}\:,\:{b}=\mathrm{4},\:{m}=\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\boldsymbol{{r}}\:=\:\frac{\mathrm{4}}{\:\sqrt{\mathrm{1}+\frac{\mathrm{32}}{\mathrm{9}}}\:}\:\:=\:\frac{\mathrm{12}}{\:\sqrt{\mathrm{41}}}\:. \\ $$
Answered by MrW3 last updated on 05/Oct/18
![eqn. of ellipse: (x^2 /a^2 )+(y^2 /b^2 )=1 ((2x)/a^2 )+((2y)/b^2 )y′=0 ⇒y′=−((b^2 x)/(a^2 y)) center of circle (x_0 ,0) with x_0 =((√(1+m^2 ))/m)r=r(√(1+(1/m^2 )))=μr contact point (u,v) u=x_0 +r cos θ=r(μ+cos θ) v=r sin θ ((r^2 (μ+cos θ)^2 )/a^2 )+((r^2 sin^2 θ)/b^2 )=1 (1/(tan θ))=((b^2 u)/(a^2 v))=((b^2 r(μ+cos θ))/(a^2 r sin θ))=((b^2 (μ+cos θ))/(a^2 sin θ)) a^2 cos θ=b^2 (μ+cos θ) (a^2 −b^2 )cos θ=μb^2 cos θ=((μb^2 )/(a^2 −b^2 ))=(μ/(λ^2 −1)) with λ=(a/b) r^2 [(((μ+cos θ)^2 )/a^2 )+((sin^2 θ)/b^2 )]=1 r^2 [((b^2 (μ+cos θ)^2 +a^2 sin^2 θ)/(a^2 b^2 ))]=1 r^2 [(((μ+(μ/(λ^2 −1)))^2 +λ^2 (1−(μ/(λ^2 −1)))(1+(μ/(λ^2 −1))))/a^2 )]=1 r^2 [(((μ^2 λ^2 (λ^2 −1)+λ^2 (λ^2 −1)^2 )/((λ^2 −1)^2 ))/a^2 )]=1 r^2 [((λ^2 (μ^2 +λ^2 −1))/(a^2 (λ^2 −1)))]=1 ⇒r=(a/λ)(√((λ^2 −1)/(μ^2 +λ^2 −1))) ⇒r=b(√((λ^2 −1)/(μ^2 +λ^2 −1))) ⇒r=b(√((((a/b))^2 −1)/(1+(1/m^2 )+((a/b))^2 −1))) ⇒r=b(√((((a/b))^2 −1)/((1/m^2 )+((a/b))^2 ))) r=(b/( (√(1+(1+(1/m^2 ))((b^2 /(a^2 −b^2 )))))))](https://www.tinkutara.com/question/Q44867.png)
$${eqn}.\:{of}\:{ellipse}: \\ $$$$\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\frac{\mathrm{2}{x}}{{a}^{\mathrm{2}} }+\frac{\mathrm{2}{y}}{{b}^{\mathrm{2}} }{y}'=\mathrm{0} \\ $$$$\Rightarrow{y}'=−\frac{{b}^{\mathrm{2}} {x}}{{a}^{\mathrm{2}} {y}} \\ $$$${center}\:{of}\:{circle}\:\left({x}_{\mathrm{0}} ,\mathrm{0}\right)\:{with} \\ $$$${x}_{\mathrm{0}} =\frac{\sqrt{\mathrm{1}+{m}^{\mathrm{2}} }}{{m}}{r}={r}\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{m}^{\mathrm{2}} }}=\mu{r} \\ $$$${contact}\:{point}\:\left({u},{v}\right) \\ $$$${u}={x}_{\mathrm{0}} +{r}\:\mathrm{cos}\:\theta={r}\left(\mu+\mathrm{cos}\:\theta\right) \\ $$$${v}={r}\:\mathrm{sin}\:\theta \\ $$$$\frac{{r}^{\mathrm{2}} \left(\mu+\mathrm{cos}\:\theta\right)^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{r}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\theta}{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\frac{\mathrm{1}}{\mathrm{tan}\:\theta}=\frac{{b}^{\mathrm{2}} {u}}{{a}^{\mathrm{2}} {v}}=\frac{{b}^{\mathrm{2}} {r}\left(\mu+\mathrm{cos}\:\theta\right)}{{a}^{\mathrm{2}} {r}\:\mathrm{sin}\:\theta}=\frac{{b}^{\mathrm{2}} \left(\mu+\mathrm{cos}\:\theta\right)}{{a}^{\mathrm{2}} \:\mathrm{sin}\:\theta} \\ $$$${a}^{\mathrm{2}} \:\mathrm{cos}\:\theta={b}^{\mathrm{2}} \left(\mu+\mathrm{cos}\:\theta\right) \\ $$$$\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\mathrm{cos}\:\theta=\mu{b}^{\mathrm{2}} \\ $$$$\mathrm{cos}\:\theta=\frac{\mu{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }=\frac{\mu}{\lambda^{\mathrm{2}} −\mathrm{1}}\:{with}\:\lambda=\frac{{a}}{{b}} \\ $$$${r}^{\mathrm{2}} \left[\frac{\left(\mu+\mathrm{cos}\:\theta\right)^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{\mathrm{sin}^{\mathrm{2}} \:\theta}{{b}^{\mathrm{2}} }\right]=\mathrm{1} \\ $$$${r}^{\mathrm{2}} \left[\frac{{b}^{\mathrm{2}} \left(\mu+\mathrm{cos}\:\theta\right)^{\mathrm{2}} +{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta}{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }\right]=\mathrm{1} \\ $$$${r}^{\mathrm{2}} \left[\frac{\left(\mu+\frac{\mu}{\lambda^{\mathrm{2}} −\mathrm{1}}\right)^{\mathrm{2}} +\lambda^{\mathrm{2}} \left(\mathrm{1}−\frac{\mu}{\lambda^{\mathrm{2}} −\mathrm{1}}\right)\left(\mathrm{1}+\frac{\mu}{\lambda^{\mathrm{2}} −\mathrm{1}}\right)}{{a}^{\mathrm{2}} }\right]=\mathrm{1} \\ $$$${r}^{\mathrm{2}} \left[\frac{\frac{\mu^{\mathrm{2}} \lambda^{\mathrm{2}} \left(\lambda^{\mathrm{2}} −\mathrm{1}\right)+\lambda^{\mathrm{2}} \left(\lambda^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }{\left(\lambda^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }}{{a}^{\mathrm{2}} }\right]=\mathrm{1} \\ $$$${r}^{\mathrm{2}} \left[\frac{\lambda^{\mathrm{2}} \left(\mu^{\mathrm{2}} +\lambda^{\mathrm{2}} −\mathrm{1}\right)}{{a}^{\mathrm{2}} \left(\lambda^{\mathrm{2}} −\mathrm{1}\right)}\right]=\mathrm{1} \\ $$$$\Rightarrow{r}=\frac{{a}}{\lambda}\sqrt{\frac{\lambda^{\mathrm{2}} −\mathrm{1}}{\mu^{\mathrm{2}} +\lambda^{\mathrm{2}} −\mathrm{1}}} \\ $$$$\Rightarrow{r}={b}\sqrt{\frac{\lambda^{\mathrm{2}} −\mathrm{1}}{\mu^{\mathrm{2}} +\lambda^{\mathrm{2}} −\mathrm{1}}} \\ $$$$\Rightarrow{r}={b}\sqrt{\frac{\left(\frac{{a}}{{b}}\right)^{\mathrm{2}} −\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{{m}^{\mathrm{2}} }+\left(\frac{{a}}{{b}}\right)^{\mathrm{2}} −\mathrm{1}}} \\ $$$$\Rightarrow{r}={b}\sqrt{\frac{\left(\frac{{a}}{{b}}\right)^{\mathrm{2}} −\mathrm{1}}{\frac{\mathrm{1}}{{m}^{\mathrm{2}} }+\left(\frac{{a}}{{b}}\right)^{\mathrm{2}} }} \\ $$$${r}=\frac{{b}}{\:\sqrt{\mathrm{1}+\left(\mathrm{1}+\frac{\mathrm{1}}{{m}^{\mathrm{2}} }\right)\left(\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }\right)}} \\ $$
Commented by ajfour last updated on 05/Oct/18
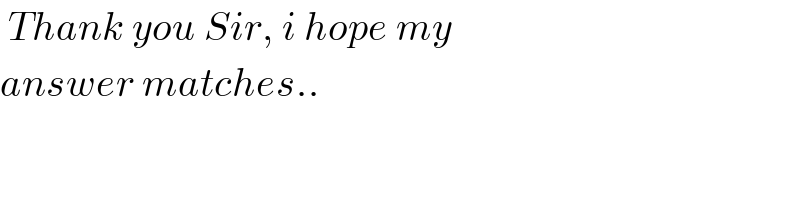
$$\:{Thank}\:{you}\:{Sir},\:{i}\:{hope}\:{my} \\ $$$${answer}\:{matches}.. \\ $$
Commented by MrW3 last updated on 05/Oct/18
$${our}\:{answers}\:{are}\:{the}\:{same}. \\ $$
