Question Number 44811 by jasno91 last updated on 05/Oct/18
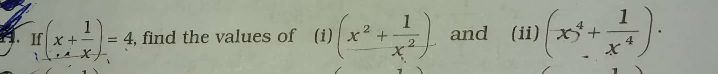
Commented by math khazana by abdo last updated on 05/Oct/18

$${x}+\frac{\mathrm{1}}{{x}}=\mathrm{4}\:\Rightarrow\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} =\mathrm{16}\:\Rightarrow{x}^{\mathrm{2}} \:+\mathrm{2}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:=\mathrm{16}\:\Rightarrow \\ $$$${x}^{\mathrm{2}} \:+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:=\mathrm{14}.{also}\:\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)^{\mathrm{2}} =\mathrm{14}^{\mathrm{2}} \:\Rightarrow \\ $$$${x}^{\mathrm{4}} \:+\mathrm{2}+\frac{\mathrm{1}}{{x}^{\mathrm{4}} }\:=\mathrm{14}^{\mathrm{2}} \:\Rightarrow{x}^{\mathrm{4}} \:+\frac{\mathrm{1}}{{x}^{\mathrm{4}} }=\mathrm{14}^{\mathrm{2}} −\mathrm{2}\:. \\ $$
