Question-44872

Question Number 44872 by ajfour last updated on 05/Oct/18

Commented by ajfour last updated on 05/Oct/18

Find equation of the rope curve, bottom end of rope is at the foot of the incline and a length b of it is in contact with the frictionless incline. Height of ceiling is h above the ground.

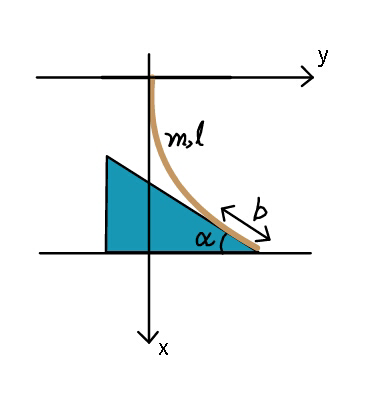
$${Find}\:{equation}\:{of}\:{the}\:{rope}\:{curve}, \\ $$$${bottom}\:{end}\:{of}\:{rope}\:{is}\:{at}\:{the}\:{foot} \\ $$$${of}\:{the}\:{incline}\:{and}\:{a}\:{length}\:\boldsymbol{{b}}\:{of}\:{it} \\ $$$${is}\:{in}\:{contact}\:{with}\:{the}\:{frictionless} \\ $$$${incline}.\:{Height}\:{of}\:{ceiling}\:{is}\:\boldsymbol{{h}} \\ $$$${above}\:{the}\:{ground}. \\ $$

Answered by MrW3 last updated on 06/Oct/18

Commented by MrW3 last updated on 08/Oct/18

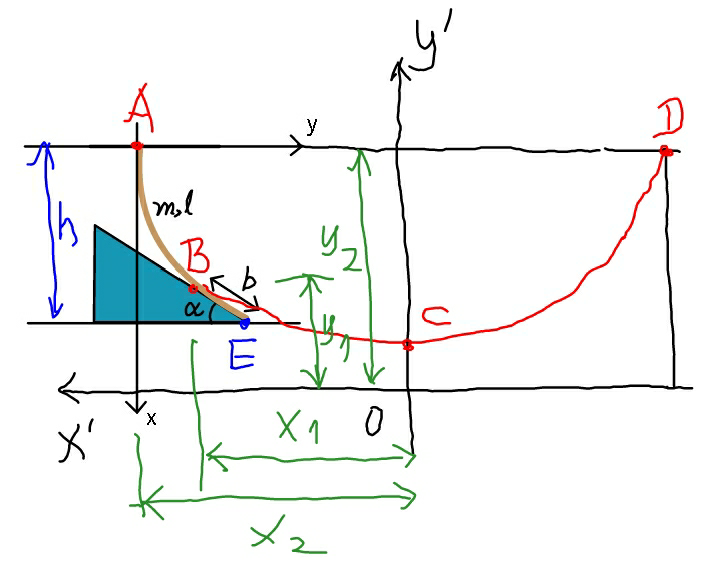
trying to solve the problem by using catenary equation directly. the hanging part of the rope AB is a part of the catenary curve ACD. let ρ=(m/l) tension in rope at point B is T=bρg sin α the horizontal component of tension in the rope AB is T_0 =T cos α=bρg sin α cos α=((bρg sin 2α)/2) the equation of rope ACD in the coordinate system x′y′ is a catenary (we use here u,v instead ofx′,y′ to avoid confusion) v=a cosh (u/a) with a=(T_0 /(ρg))=((bρg sin 2α)/(2ρg))=(1/2)b sin 2α length of rope upon point C is s=a sinh (u/a) inclination of rope is (dv/du)=sinh (u/a) at point B: tan α=(dv/du)=sinh (x_1 /a) ⇒x_1 =a sinh^(−1) (tan α) ⇒y_1 =a cosh (x_1 /a)=a cosh {sinh^(−1) (tan α)} CB^(⌢) =s_1 =a sinh (x_1 /a)=a tan α CA^(⌢) =s_2 =a sinh (x_2 /a) s_2 −s_1 =AB^(⌢) =l−b a sinh (x_2 /a)−a tan α=l−b sinh (x_2 /a)=tan α+((l−b)/a) ⇒x_2 =a sinh^(−1) (tan α+((l−b)/a)) ⇒y_2 =a cosh (x_2 /a)=a cosh {sinh^(−1) (tan α+((l−b)/a))} ⇒ΔH=x_2 −x_1 =a {sinh^(−1) (tan α+((l−b)/a))−sinh^(−1) (tan α)} ⇒ΔV=y_2 −y_1 =a[cosh {sinh^(−1) (tan α+((l−b)/a))}−cosh {sinh^(−1) (tan α)}] eqn. of rope AB in the requested coordinate system xy: u=x_2 −y=a sinh^(−1) (tan α+((l−b)/a))−y v=y_2 −x=a cosh {sinh^(−1) (tan α+((l−b)/a))}−x putting this into v=a cosh (u/a) we can get following eqn. for rope curve AB: a cosh {sinh^(−1) (tan α+((l−b)/a))}−x=a cosh ((a sinh^(−1) (tan α+((l−b)/a))−y)/a) or (x/a)=cosh {sinh^(−1) (tan α+((l−b)/a))}−cosh {sinh^(−1) (tan α+((l−b)/a))−(y/a)} or (y/a)=sinh^(−1) (tan α+((l−b)/a))−cosh^(−1) [cosh {sinh^(−1) (tan α+((l−b)/a))}−(x/a)] with a=(1/2)b sin 2α and it′s valid for 0≤x≤ΔV and 0≤y≤ΔH

$${trying}\:{to}\:{solve}\:{the}\:{problem}\:{by}\:{using} \\ $$$${catenary}\:{equation}\:{directly}. \\ $$$$ \\ $$$${the}\:{hanging}\:{part}\:{of}\:{the}\:{rope}\:{AB}\:{is}\:{a} \\ $$$${part}\:{of}\:{the}\:{catenary}\:\:{curve}\:{ACD}. \\ $$$${let}\:\rho=\frac{{m}}{{l}} \\ $$$${tension}\:{in}\:{rope}\:{at}\:{point}\:{B}\:{is} \\ $$$${T}={b}\rho{g}\:\mathrm{sin}\:\alpha \\ $$$${the}\:{horizontal}\:{component}\:{of}\:{tension} \\ $$$${in}\:{the}\:{rope}\:{AB}\:{is} \\ $$$${T}_{\mathrm{0}} ={T}\:\mathrm{cos}\:\alpha={b}\rho{g}\:\mathrm{sin}\:\alpha\:\mathrm{cos}\:\alpha=\frac{{b}\rho{g}\:\mathrm{sin}\:\mathrm{2}\alpha}{\mathrm{2}} \\ $$$$ \\ $$$${the}\:{equation}\:{of}\:{rope}\:{ACD}\:{in}\:{the} \\ $$$${coordinate}\:{system}\:{x}'{y}'\:{is}\:{a}\:{catenary} \\ $$$$\left({we}\:{use}\:{here}\:{u},{v}\:{instead}\:{ofx}',{y}'\:{to}\:{avoid}\right. \\ $$$$\left.{confusion}\right) \\ $$$${v}={a}\:\mathrm{cosh}\:\frac{{u}}{{a}}\:{with} \\ $$$${a}=\frac{{T}_{\mathrm{0}} }{\rho{g}}=\frac{{b}\rho{g}\:\mathrm{sin}\:\mathrm{2}\alpha}{\mathrm{2}\rho{g}}=\frac{\mathrm{1}}{\mathrm{2}}{b}\:\mathrm{sin}\:\mathrm{2}\alpha \\ $$$$ \\ $$$${length}\:{of}\:{rope}\:{upon}\:{point}\:{C}\:{is} \\ $$$${s}={a}\:\mathrm{sinh}\:\frac{{u}}{{a}} \\ $$$$ \\ $$$${inclination}\:{of}\:{rope}\:{is} \\ $$$$\frac{{dv}}{{du}}=\mathrm{sinh}\:\frac{{u}}{{a}} \\ $$$$ \\ $$$${at}\:{point}\:{B}: \\ $$$$\mathrm{tan}\:\alpha=\frac{{dv}}{{du}}=\mathrm{sinh}\:\frac{{x}_{\mathrm{1}} }{{a}} \\ $$$$\Rightarrow{x}_{\mathrm{1}} ={a}\:\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\alpha\right) \\ $$$$\Rightarrow{y}_{\mathrm{1}} ={a}\:\mathrm{cosh}\:\frac{{x}_{\mathrm{1}} }{{a}}={a}\:\mathrm{cosh}\:\left\{\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\alpha\right)\right\} \\ $$$$ \\ $$$$\overset{\frown} {{CB}}={s}_{\mathrm{1}} ={a}\:\mathrm{sinh}\:\frac{{x}_{\mathrm{1}} }{{a}}={a}\:\mathrm{tan}\:\alpha \\ $$$$\overset{\frown} {{CA}}={s}_{\mathrm{2}} ={a}\:\mathrm{sinh}\:\frac{{x}_{\mathrm{2}} }{{a}} \\ $$$${s}_{\mathrm{2}} −{s}_{\mathrm{1}} =\overset{\frown} {{AB}}={l}−{b} \\ $$$${a}\:\mathrm{sinh}\:\frac{{x}_{\mathrm{2}} }{{a}}−{a}\:\mathrm{tan}\:\alpha={l}−{b} \\ $$$$\:\mathrm{sinh}\:\frac{{x}_{\mathrm{2}} }{{a}}=\mathrm{tan}\:\alpha+\frac{{l}−{b}}{{a}} \\ $$$$\Rightarrow{x}_{\mathrm{2}} ={a}\:\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\alpha+\frac{{l}−{b}}{{a}}\right) \\ $$$$\Rightarrow{y}_{\mathrm{2}} ={a}\:\mathrm{cosh}\:\frac{{x}_{\mathrm{2}} }{{a}}={a}\:\mathrm{cosh}\:\left\{\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\alpha+\frac{{l}−{b}}{{a}}\right)\right\} \\ $$$$ \\ $$$$\Rightarrow\Delta{H}={x}_{\mathrm{2}} −{x}_{\mathrm{1}} ={a}\:\left\{\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\alpha+\frac{{l}−{b}}{{a}}\right)−\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\alpha\right)\right\} \\ $$$$\Rightarrow\Delta{V}={y}_{\mathrm{2}} −{y}_{\mathrm{1}} ={a}\left[\mathrm{cosh}\:\left\{\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\alpha+\frac{{l}−{b}}{{a}}\right)\right\}−\mathrm{cosh}\:\left\{\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\alpha\right)\right\}\right] \\ $$$$ \\ $$$${eqn}.\:{of}\:{rope}\:{AB}\:{in}\:{the}\:{requested} \\ $$$${coordinate}\:{system}\:{xy}: \\ $$$${u}={x}_{\mathrm{2}} −{y}={a}\:\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\alpha+\frac{{l}−{b}}{{a}}\right)−{y} \\ $$$${v}={y}_{\mathrm{2}} −{x}={a}\:\mathrm{cosh}\:\left\{\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\alpha+\frac{{l}−{b}}{{a}}\right)\right\}−{x} \\ $$$${putting}\:{this}\:{into}\:{v}={a}\:\mathrm{cosh}\:\frac{{u}}{{a}}\:{we}\:{can}\:{get} \\ $$$${following}\:{eqn}.\:{for}\:{rope}\:{curve}\:{AB}: \\ $$$${a}\:\mathrm{cosh}\:\left\{\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\alpha+\frac{{l}−{b}}{{a}}\right)\right\}−{x}={a}\:\mathrm{cosh}\:\frac{{a}\:\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\alpha+\frac{{l}−{b}}{{a}}\right)−{y}}{{a}} \\ $$$${or} \\ $$$$\frac{{x}}{{a}}=\mathrm{cosh}\:\left\{\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\alpha+\frac{{l}−{b}}{{a}}\right)\right\}−\mathrm{cosh}\:\left\{\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\alpha+\frac{{l}−{b}}{{a}}\right)−\frac{{y}}{{a}}\right\} \\ $$$${or} \\ $$$$\frac{{y}}{{a}}=\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\alpha+\frac{{l}−{b}}{{a}}\right)−\mathrm{cosh}^{−\mathrm{1}} \:\left[\mathrm{cosh}\:\left\{\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\alpha+\frac{{l}−{b}}{{a}}\right)\right\}−\frac{{x}}{{a}}\right] \\ $$$${with}\:{a}=\frac{\mathrm{1}}{\mathrm{2}}{b}\:\mathrm{sin}\:\mathrm{2}\alpha\:{and}\:{it}'{s}\:{valid} \\ $$$${for}\:\mathrm{0}\leqslant{x}\leqslant\Delta{V}\:{and}\:\mathrm{0}\leqslant{y}\leqslant\Delta{H} \\ $$

Commented by MrW3 last updated on 06/Oct/18