Question Number 44900 by peter frank last updated on 06/Oct/18

Answered by MJS last updated on 06/Oct/18
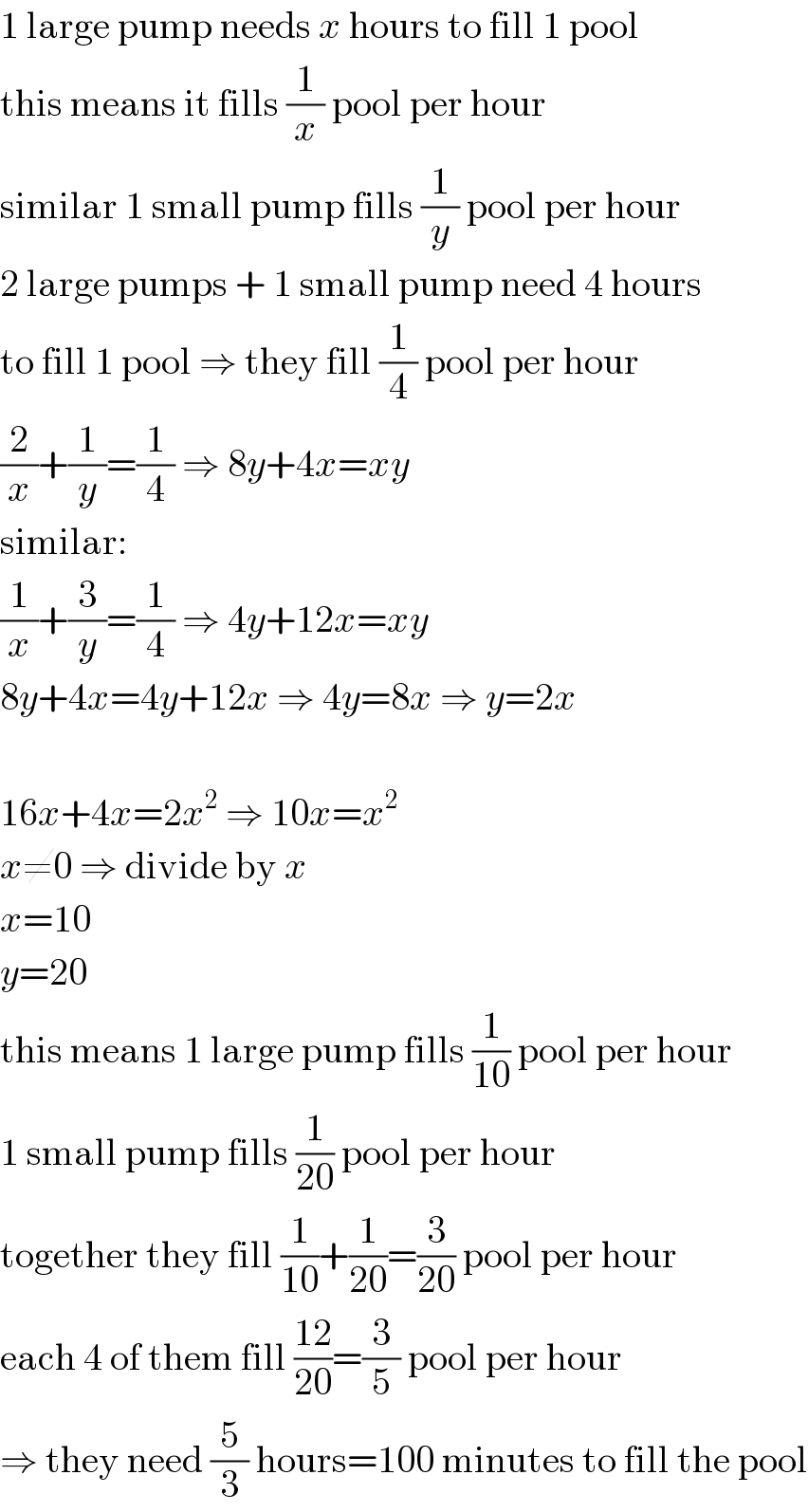
$$\mathrm{1}\:\mathrm{large}\:\mathrm{pump}\:\mathrm{needs}\:{x}\:\mathrm{hours}\:\mathrm{to}\:\mathrm{fill}\:\mathrm{1}\:\mathrm{pool} \\ $$$$\mathrm{this}\:\mathrm{means}\:\mathrm{it}\:\mathrm{fills}\:\frac{\mathrm{1}}{{x}}\:\mathrm{pool}\:\mathrm{per}\:\mathrm{hour} \\ $$$$\mathrm{similar}\:\mathrm{1}\:\mathrm{small}\:\mathrm{pump}\:\mathrm{fills}\:\frac{\mathrm{1}}{{y}}\:\mathrm{pool}\:\mathrm{per}\:\mathrm{hour} \\ $$$$\mathrm{2}\:\mathrm{large}\:\mathrm{pumps}\:+\:\mathrm{1}\:\mathrm{small}\:\mathrm{pump}\:\mathrm{need}\:\mathrm{4}\:\mathrm{hours} \\ $$$$\mathrm{to}\:\mathrm{fill}\:\mathrm{1}\:\mathrm{pool}\:\Rightarrow\:\mathrm{they}\:\mathrm{fill}\:\frac{\mathrm{1}}{\mathrm{4}}\:\mathrm{pool}\:\mathrm{per}\:\mathrm{hour} \\ $$$$\frac{\mathrm{2}}{{x}}+\frac{\mathrm{1}}{{y}}=\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow\:\mathrm{8}{y}+\mathrm{4}{x}={xy} \\ $$$$\mathrm{similar}: \\ $$$$\frac{\mathrm{1}}{{x}}+\frac{\mathrm{3}}{{y}}=\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow\:\mathrm{4}{y}+\mathrm{12}{x}={xy} \\ $$$$\mathrm{8}{y}+\mathrm{4}{x}=\mathrm{4}{y}+\mathrm{12}{x}\:\Rightarrow\:\mathrm{4}{y}=\mathrm{8}{x}\:\Rightarrow\:{y}=\mathrm{2}{x} \\ $$$$ \\ $$$$\mathrm{16}{x}+\mathrm{4}{x}=\mathrm{2}{x}^{\mathrm{2}} \:\Rightarrow\:\mathrm{10}{x}={x}^{\mathrm{2}} \\ $$$${x}\neq\mathrm{0}\:\Rightarrow\:\mathrm{divide}\:\mathrm{by}\:{x} \\ $$$${x}=\mathrm{10} \\ $$$${y}=\mathrm{20} \\ $$$$\mathrm{this}\:\mathrm{means}\:\mathrm{1}\:\mathrm{large}\:\mathrm{pump}\:\mathrm{fills}\:\frac{\mathrm{1}}{\mathrm{10}}\:\mathrm{pool}\:\mathrm{per}\:\mathrm{hour} \\ $$$$\mathrm{1}\:\mathrm{small}\:\mathrm{pump}\:\mathrm{fills}\:\frac{\mathrm{1}}{\mathrm{20}}\:\mathrm{pool}\:\mathrm{per}\:\mathrm{hour} \\ $$$$\mathrm{together}\:\mathrm{they}\:\mathrm{fill}\:\frac{\mathrm{1}}{\mathrm{10}}+\frac{\mathrm{1}}{\mathrm{20}}=\frac{\mathrm{3}}{\mathrm{20}}\:\mathrm{pool}\:\mathrm{per}\:\mathrm{hour} \\ $$$$\mathrm{each}\:\mathrm{4}\:\mathrm{of}\:\mathrm{them}\:\mathrm{fill}\:\frac{\mathrm{12}}{\mathrm{20}}=\frac{\mathrm{3}}{\mathrm{5}}\:\mathrm{pool}\:\mathrm{per}\:\mathrm{hour} \\ $$$$\Rightarrow\:\mathrm{they}\:\mathrm{need}\:\frac{\mathrm{5}}{\mathrm{3}}\:\mathrm{hours}=\mathrm{100}\:\mathrm{minutes}\:\mathrm{to}\:\mathrm{fill}\:\mathrm{the}\:\mathrm{pool} \\ $$
Commented by peter frank last updated on 06/Oct/18

$$\mathrm{thanks}\:\mathrm{sir} \\ $$
