Question Number 44928 by rahul 19 last updated on 06/Oct/18

Commented by rahul 19 last updated on 06/Oct/18
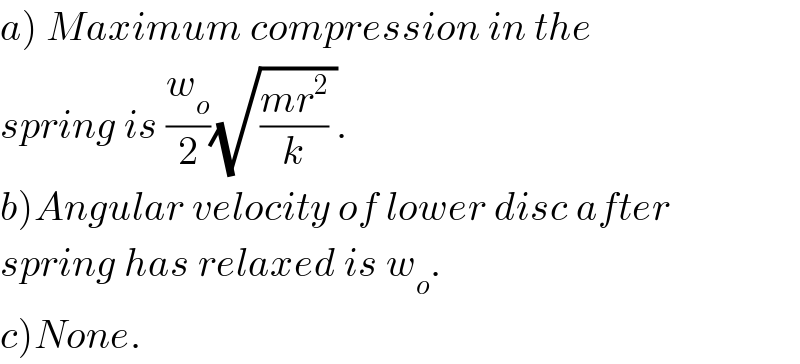
$$\left.{a}\right)\:{Maximum}\:{compression}\:{in}\:{the} \\ $$$${spring}\:{is}\:\frac{{w}_{{o}} }{\mathrm{2}}\sqrt{\frac{{mr}^{\mathrm{2}} }{{k}}\:}. \\ $$$$\left.{b}\right){Angular}\:{velocity}\:{of}\:{lower}\:{disc}\:{after} \\ $$$${spring}\:{has}\:{relaxed}\:{is}\:{w}_{{o}} . \\ $$$$\left.{c}\right){None}. \\ $$
Commented by MrW3 last updated on 06/Oct/18

$$\left.{a}\right) \\ $$$${max}.\:{compression}\:{in}\:{spring}\:={d} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{kd}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}×\frac{{mr}^{\mathrm{2}} }{\mathrm{2}}×\omega_{\mathrm{0}} ^{\mathrm{2}} \\ $$$$\Rightarrow{d}=\omega_{\mathrm{0}} \sqrt{\frac{{mr}^{\mathrm{2}} }{\mathrm{2}{k}}} \\ $$$$\left.\Rightarrow{option}\:{a}\right)\:{is}\:{wrong} \\ $$$$\left.{b}\right) \\ $$$${after}\:{the}\:{spring}\:{has}\:{relaxed}\:{again}\:{both} \\ $$$${discs}\:{have}\:{the}\:{same}\:{angular}\:{velocity}\:\omega \\ $$$$\mathrm{2}×\frac{\mathrm{1}}{\mathrm{2}}×\frac{{mr}^{\mathrm{2}} }{\mathrm{2}}×\omega^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}×\frac{{mr}^{\mathrm{2}} }{\mathrm{2}}×\omega_{\mathrm{0}} ^{\mathrm{2}} \\ $$$$\Rightarrow\omega=\frac{\omega_{\mathrm{0}} }{\:\sqrt{\mathrm{2}}} \\ $$$$\left.\Rightarrow{option}\:{b}\right)\:{is}\:{wrong} \\ $$$$ \\ $$$$\left.\Rightarrow{answer}\:{is}\:{c}\right) \\ $$
Commented by rahul 19 last updated on 06/Oct/18

$${thanks}\:{sir}! \\ $$
