Menu Close

Question-44950

Tinku Tara 0 Comments
Pin




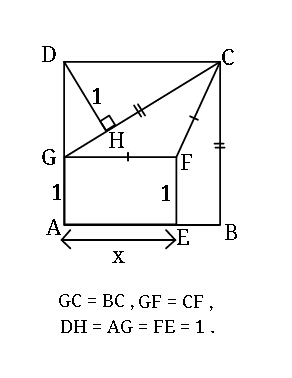
Question Number 44950 by ajfour last updated on 06/Oct/18
Commented by ajfour last updated on 06/Oct/18
Commented by ajfour last updated on 06/Oct/18
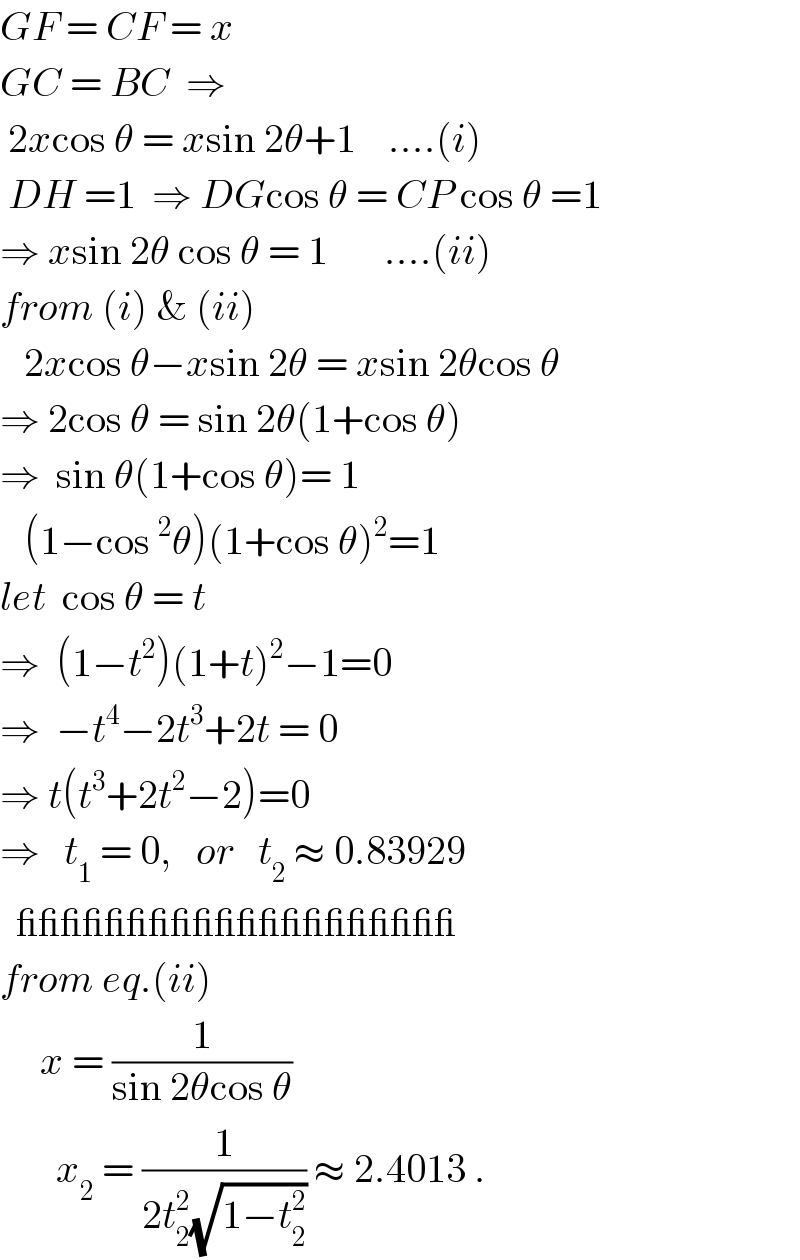
GF = CF = x GC = BC ⇒ 2xcos θ = xsin 2θ+1 ....(i) DH =1 ⇒ DGcos θ = CP cos θ =1 ⇒ xsin 2θ cos θ = 1 ....(ii) from (i) & (ii) 2xcos θ−xsin 2θ = xsin 2θcos θ ⇒ 2cos θ = sin 2θ(1+cos θ) ⇒ sin θ(1+cos θ)= 1 (1−cos^2 θ)(1+cos θ)^2 =1 let cos θ = t ⇒ (1−t^2 )(1+t)^2 −1=0 ⇒ −t^4 −2t^3 +2t = 0 ⇒ t(t^3 +2t^2 −2)=0 ⇒ t_1 = 0, or t_2 ≈ 0.83929 ____________________ from eq.(ii) x = (1/(sin 2θcos θ)) x_2 = (1/(2t_2 ^2 (√(1−t_2 ^2 )))) ≈ 2.4013 .
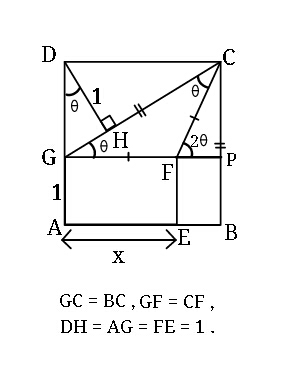
$${GF}\:=\:{CF}\:=\:{x} \\ $$$${GC}\:=\:{BC}\:\:\Rightarrow \\ $$$$\:\mathrm{2}{x}\mathrm{cos}\:\theta\:=\:{x}\mathrm{sin}\:\mathrm{2}\theta+\mathrm{1}\:\:\:\:….\left({i}\right) \\ $$$$\:{DH}\:=\mathrm{1}\:\:\Rightarrow\:{DG}\mathrm{cos}\:\theta\:=\:{CP}\:\mathrm{cos}\:\theta\:=\mathrm{1} \\ $$$$\Rightarrow\:{x}\mathrm{sin}\:\mathrm{2}\theta\:\mathrm{cos}\:\theta\:=\:\mathrm{1}\:\:\:\:\:\:\:….\left({ii}\right) \\ $$$${from}\:\left({i}\right)\:\&\:\left({ii}\right) \\ $$$$\:\:\:\mathrm{2}{x}\mathrm{cos}\:\theta−{x}\mathrm{sin}\:\mathrm{2}\theta\:=\:{x}\mathrm{sin}\:\mathrm{2}\theta\mathrm{cos}\:\theta \\ $$$$\Rightarrow\:\mathrm{2cos}\:\theta\:=\:\mathrm{sin}\:\mathrm{2}\theta\left(\mathrm{1}+\mathrm{cos}\:\theta\right) \\ $$$$\Rightarrow\:\:\mathrm{sin}\:\theta\left(\mathrm{1}+\mathrm{cos}\:\theta\right)=\:\mathrm{1} \\ $$$$\:\:\:\left(\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} \theta\right)\left(\mathrm{1}+\mathrm{cos}\:\theta\right)^{\mathrm{2}} =\mathrm{1} \\ $$$${let}\:\:\mathrm{cos}\:\theta\:=\:{t} \\ $$$$\Rightarrow\:\:\left(\mathrm{1}−{t}^{\mathrm{2}} \right)\left(\mathrm{1}+{t}\right)^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\:\:−{t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{3}} +\mathrm{2}{t}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:{t}\left({t}^{\mathrm{3}} +\mathrm{2}{t}^{\mathrm{2}} −\mathrm{2}\right)=\mathrm{0} \\ $$$$\Rightarrow\:\:\:{t}_{\mathrm{1}} \:=\:\mathrm{0},\:\:\:{or}\:\:\:{t}_{\mathrm{2}} \:\approx\:\mathrm{0}.\mathrm{83929} \\ $$$$\:\:\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$${from}\:{eq}.\left({ii}\right) \\ $$$$\:\:\:\:\:{x}\:=\:\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{2}\theta\mathrm{cos}\:\theta} \\ $$$$\:\:\:\:\:\:\:{x}_{\mathrm{2}} \:=\:\frac{\mathrm{1}}{\mathrm{2}{t}_{\mathrm{2}} ^{\mathrm{2}} \sqrt{\mathrm{1}−{t}_{\mathrm{2}} ^{\mathrm{2}} }}\:\approx\:\mathrm{2}.\mathrm{4013}\:. \\ $$
Commented by MrW3 last updated on 07/Oct/18
congratulations to your skill for solving cubic equations sir!
$${congratulations}\:{to}\:{your}\:{skill}\:{for} \\ $$$${solving}\:{cubic}\:{equations}\:{sir}! \\ $$
Commented by MJS last updated on 09/Oct/18
great! just a calculation error in the last line. it must be x_2 ≈1.30557
$$\mathrm{great}! \\ $$$$\mathrm{just}\:\mathrm{a}\:\mathrm{calculation}\:\mathrm{error}\:\mathrm{in}\:\mathrm{the}\:\mathrm{last}\:\mathrm{line}.\:\mathrm{it}\:\mathrm{must}\:\mathrm{be} \\ $$$${x}_{\mathrm{2}} \approx\mathrm{1}.\mathrm{30557} \\ $$
Answered by MJS last updated on 09/Oct/18
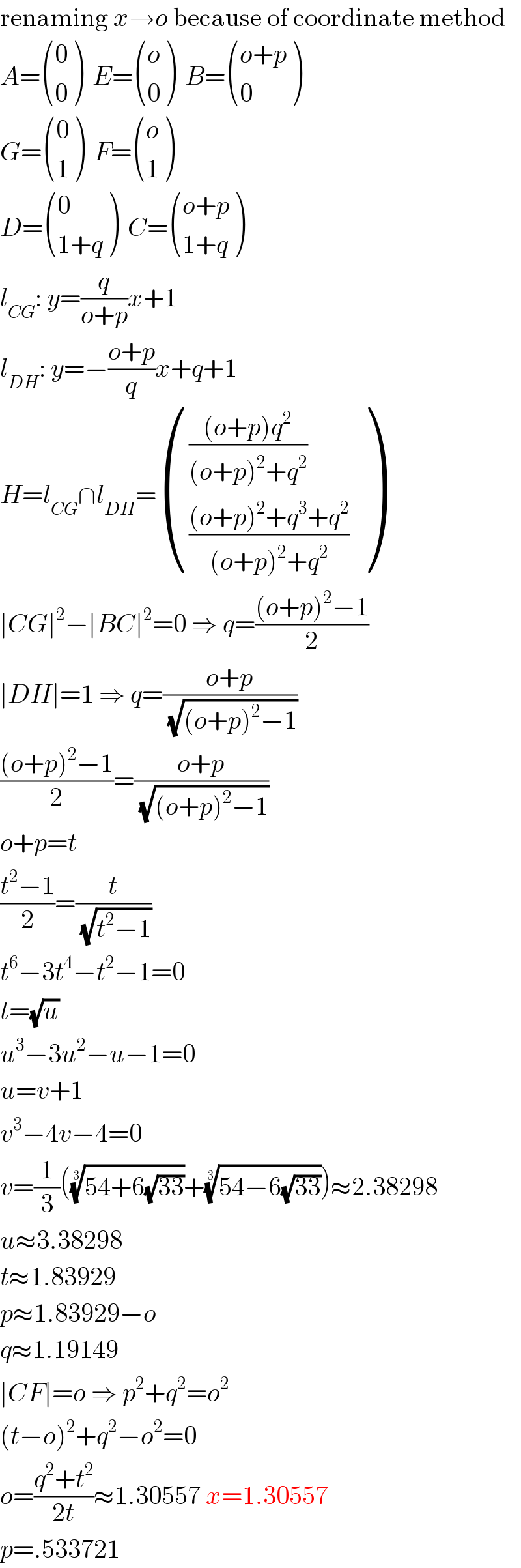
renaming x→o because of coordinate method A= ((0),(0) ) E= ((o),(0) ) B= (((o+p)),(0) ) G= ((0),(1) ) F= ((o),(1) ) D= ((0),((1+q)) ) C= (((o+p)),((1+q)) ) l_(CG) : y=(q/(o+p))x+1 l_(DH) : y=−((o+p)/q)x+q+1 H=l_(CG) ∩l_(DH) = (((((o+p)q^2 )/((o+p)^2 +q^2 ))),((((o+p)^2 +q^3 +q^2 )/((o+p)^2 +q^2 ))) ) ∣CG∣^2 −∣BC∣^2 =0 ⇒ q=(((o+p)^2 −1)/2) ∣DH∣=1 ⇒ q=((o+p)/( (√((o+p)^2 −1)))) (((o+p)^2 −1)/2)=((o+p)/( (√((o+p)^2 −1)))) o+p=t ((t^2 −1)/2)=(t/( (√(t^2 −1)))) t^6 −3t^4 −t^2 −1=0 t=(√u) u^3 −3u^2 −u−1=0 u=v+1 v^3 −4v−4=0 v=(1/3)(((54+6(√(33))))^(1/3) +((54−6(√(33))))^(1/3) )≈2.38298 u≈3.38298 t≈1.83929 p≈1.83929−o q≈1.19149 ∣CF∣=o ⇒ p^2 +q^2 =o^2 (t−o)^2 +q^2 −o^2 =0 o=((q^2 +t^2 )/(2t))≈1.30557 x=1.30557 p=.533721
$$\mathrm{renaming}\:{x}\rightarrow{o}\:\mathrm{because}\:\mathrm{of}\:\mathrm{coordinate}\:\mathrm{method} \\ $$$${A}=\begin{pmatrix}{\mathrm{0}}\\{\mathrm{0}}\end{pmatrix}\:\:{E}=\begin{pmatrix}{{o}}\\{\mathrm{0}}\end{pmatrix}\:\:{B}=\begin{pmatrix}{{o}+{p}}\\{\mathrm{0}}\end{pmatrix} \\ $$$${G}=\begin{pmatrix}{\mathrm{0}}\\{\mathrm{1}}\end{pmatrix}\:\:{F}=\begin{pmatrix}{{o}}\\{\mathrm{1}}\end{pmatrix} \\ $$$${D}=\begin{pmatrix}{\mathrm{0}}\\{\mathrm{1}+{q}}\end{pmatrix}\:\:{C}=\begin{pmatrix}{{o}+{p}}\\{\mathrm{1}+{q}}\end{pmatrix} \\ $$$${l}_{{CG}} :\:{y}=\frac{{q}}{{o}+{p}}{x}+\mathrm{1} \\ $$$${l}_{{DH}} :\:{y}=−\frac{{o}+{p}}{{q}}{x}+{q}+\mathrm{1} \\ $$$${H}={l}_{{CG}} \cap{l}_{{DH}} =\begin{pmatrix}{\frac{\left({o}+{p}\right){q}^{\mathrm{2}} }{\left({o}+{p}\right)^{\mathrm{2}} +{q}^{\mathrm{2}} }}\\{\frac{\left({o}+{p}\right)^{\mathrm{2}} +{q}^{\mathrm{3}} +{q}^{\mathrm{2}} }{\left({o}+{p}\right)^{\mathrm{2}} +{q}^{\mathrm{2}} }}\end{pmatrix} \\ $$$$\mid{CG}\mid^{\mathrm{2}} −\mid{BC}\mid^{\mathrm{2}} =\mathrm{0}\:\Rightarrow\:{q}=\frac{\left({o}+{p}\right)^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}} \\ $$$$\mid{DH}\mid=\mathrm{1}\:\Rightarrow\:{q}=\frac{{o}+{p}}{\:\sqrt{\left({o}+{p}\right)^{\mathrm{2}} −\mathrm{1}}} \\ $$$$\frac{\left({o}+{p}\right)^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}}=\frac{{o}+{p}}{\:\sqrt{\left({o}+{p}\right)^{\mathrm{2}} −\mathrm{1}}} \\ $$$${o}+{p}={t} \\ $$$$\frac{{t}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}}=\frac{{t}}{\:\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}} \\ $$$${t}^{\mathrm{6}} −\mathrm{3}{t}^{\mathrm{4}} −{t}^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$$${t}=\sqrt{{u}} \\ $$$${u}^{\mathrm{3}} −\mathrm{3}{u}^{\mathrm{2}} −{u}−\mathrm{1}=\mathrm{0} \\ $$$${u}={v}+\mathrm{1} \\ $$$${v}^{\mathrm{3}} −\mathrm{4}{v}−\mathrm{4}=\mathrm{0} \\ $$$${v}=\frac{\mathrm{1}}{\mathrm{3}}\left(\sqrt[{\mathrm{3}}]{\mathrm{54}+\mathrm{6}\sqrt{\mathrm{33}}}+\sqrt[{\mathrm{3}}]{\mathrm{54}−\mathrm{6}\sqrt{\mathrm{33}}}\right)\approx\mathrm{2}.\mathrm{38298} \\ $$$${u}\approx\mathrm{3}.\mathrm{38298} \\ $$$${t}\approx\mathrm{1}.\mathrm{83929} \\ $$$${p}\approx\mathrm{1}.\mathrm{83929}−{o} \\ $$$${q}\approx\mathrm{1}.\mathrm{19149} \\ $$$$\mid{CF}\mid={o}\:\Rightarrow\:{p}^{\mathrm{2}} +{q}^{\mathrm{2}} ={o}^{\mathrm{2}} \\ $$$$\left({t}−{o}\right)^{\mathrm{2}} +{q}^{\mathrm{2}} −{o}^{\mathrm{2}} =\mathrm{0} \\ $$$${o}=\frac{{q}^{\mathrm{2}} +{t}^{\mathrm{2}} }{\mathrm{2}{t}}\approx\mathrm{1}.\mathrm{30557}\:{x}=\mathrm{1}.\mathrm{30557} \\ $$$${p}=.\mathrm{533721} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *