Question Number 44951 by rahul 19 last updated on 06/Oct/18

Commented by rahul 19 last updated on 07/Oct/18
Commented by rahul 19 last updated on 07/Oct/18
$${pls}\:{explain}\:{the}\:{solution}!\left(\mathrm{1}^{{st}} ,\mathrm{2}^{{nd}} {line}\right) \\ $$
Commented by MrW3 last updated on 07/Oct/18

$${the}\:{solution}\:{given}\:{is}\:{not}\:{correct},\:{I}\:{think}. \\ $$$${it}\:{ignores}\:{the}\:{friction}\:{caused}\:{through} \\ $$$${the}\:{tension}\:{in}\:{the}\:{rope}. \\ $$
Answered by MrW3 last updated on 06/Oct/18
Commented by rahul 19 last updated on 07/Oct/18
sir, Ans. is AD
I feel the solution is too advance for me . Anyways Thanks!!☺️��
Commented by MrW3 last updated on 07/Oct/18
Commented by MrW3 last updated on 07/Oct/18
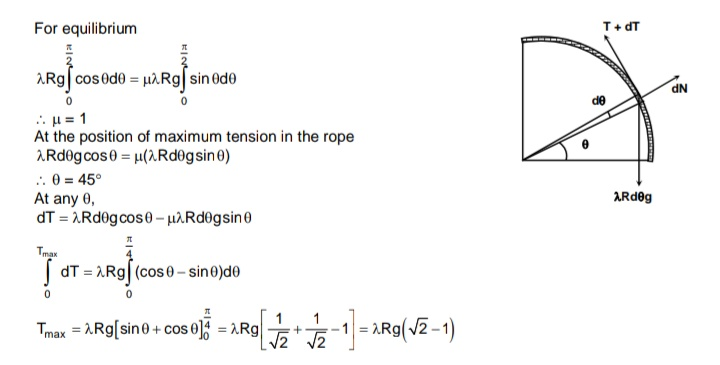
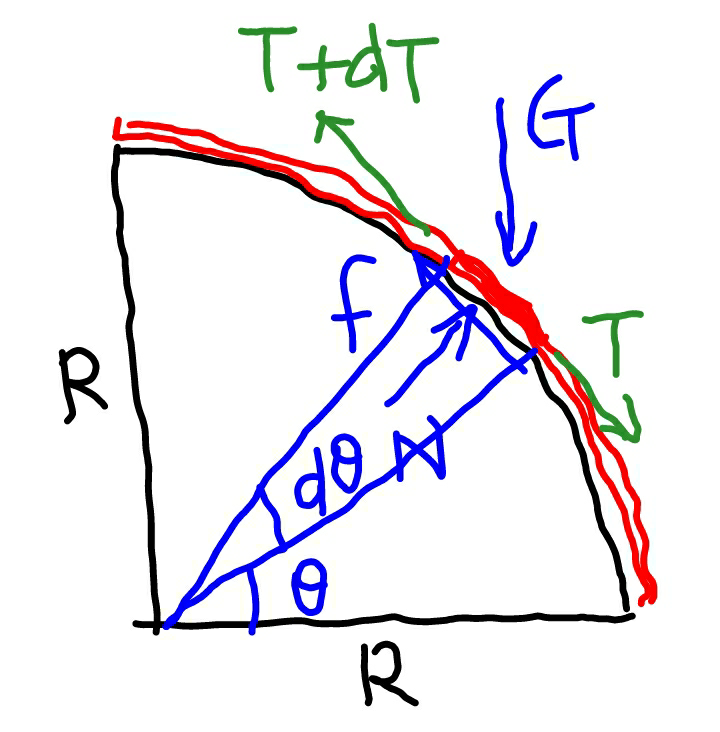
![G=λgds=λgRdθ N=(T/R)ds+G sin θ=(T+λgR sin θ)dθ f=μN=μ(T+λgR sin θ)dθ T+dT+f=T+G cos θ dT+μ(T+λgR sin θ)dθ=λgR cos θ dθ ⇒(dT/dθ)+μT=λgR(cos θ−μ sin θ) let T=e^(−μθ) S (dT/dθ)=−μe^(−μθ) S+e^(−μθ) (dS/dθ) −μe^(−μθ) S+e^(−μθ) (dS/dθ)+μe^(−μθ) S=λgR(cos θ−μ sin θ) e^(−μθ) (dS/dθ)=λgR(cos θ−μ sin θ) ⇒(dS/dθ)=λgRe^(μθ) (cos θ−μ sin θ) S=λgR∫e^(μθ) (cos θ−μ sin θ)dθ =((λgRe^(μθ) {2μ cos θ+(1−μ^2 )sin θ})/(1+μ^2 ))+C e^(μθ) T=((λgRe^(μθ) {2μ cos θ+(1−μ^2 )sin θ})/(1+μ^2 ))+C ⇒T=((λgR{2μ cos θ+(1−μ^2 )sin θ})/(1+μ^2 ))+Ce^(−μθ) at θ=0: T=0 ((2λgRμ)/(1+μ^2 ))+C=0 C=−((2λgRμ)/(1+μ^2 )) ⇒T=((λgR)/(1+μ^2 ))[(1−μ^2 ) sin θ+2μ(cos θ−e^(−μθ) )] the friction coeifficient is big enough if no tension force is needed to hold the rope at its topmost point. at θ=(π/2): T=^(!) 0 ((λgR)/(1+μ^2 ))(1−μ^2 −2μe^(−((μπ)/2)) )=0 ⇒1−μ^2 −2μe^(−((μπ)/2)) =0 ⇒μ≈0.7324 [Option B gives (1/( (√2)))=0.707] (dT/dθ)=...[(1−μ^2 )cos θ+2μ(−sin θ+μe^(−μθ) )]=0 ⇒((sin θ−μe^(−μθ) )/(cos θ))=((1−μ^2 )/(2μ)) ⇒θ in terms of μ with μ=0.7324⇒θ=41.74° ⇒T_(max) =0.353λRg [Option D gives ((√2)−1)λRg=0.414λRg]](https://www.tinkutara.com/question/Q44957.png)
$${G}=\lambda{gds}=\lambda{gRd}\theta \\ $$$${N}=\frac{{T}}{{R}}{ds}+{G}\:\mathrm{sin}\:\theta=\left({T}+\lambda{gR}\:\mathrm{sin}\:\theta\right){d}\theta \\ $$$${f}=\mu{N}=\mu\left({T}+\lambda{gR}\:\mathrm{sin}\:\theta\right){d}\theta \\ $$$${T}+{dT}+{f}={T}+{G}\:\mathrm{cos}\:\theta \\ $$$${dT}+\mu\left({T}+\lambda{gR}\:\mathrm{sin}\:\theta\right){d}\theta=\lambda{gR}\:\mathrm{cos}\:\theta\:{d}\theta \\ $$$$\Rightarrow\frac{{dT}}{{d}\theta}+\mu{T}=\lambda{gR}\left(\mathrm{cos}\:\theta−\mu\:\mathrm{sin}\:\theta\right) \\ $$$${let}\:{T}={e}^{−\mu\theta} {S} \\ $$$$\frac{{dT}}{{d}\theta}=−\mu{e}^{−\mu\theta} {S}+{e}^{−\mu\theta} \frac{{dS}}{{d}\theta} \\ $$$$−\mu{e}^{−\mu\theta} {S}+{e}^{−\mu\theta} \frac{{dS}}{{d}\theta}+\mu{e}^{−\mu\theta} {S}=\lambda{gR}\left(\mathrm{cos}\:\theta−\mu\:\mathrm{sin}\:\theta\right) \\ $$$${e}^{−\mu\theta} \frac{{dS}}{{d}\theta}=\lambda{gR}\left(\mathrm{cos}\:\theta−\mu\:\mathrm{sin}\:\theta\right) \\ $$$$\Rightarrow\frac{{dS}}{{d}\theta}=\lambda{gRe}^{\mu\theta} \left(\mathrm{cos}\:\theta−\mu\:\mathrm{sin}\:\theta\right) \\ $$$${S}=\lambda{gR}\int{e}^{\mu\theta} \:\left(\mathrm{cos}\:\theta−\mu\:\mathrm{sin}\:\theta\right){d}\theta \\ $$$$=\frac{\lambda{gRe}^{\mu\theta} \left\{\mathrm{2}\mu\:\mathrm{cos}\:\theta+\left(\mathrm{1}−\mu^{\mathrm{2}} \right)\mathrm{sin}\:\theta\right\}}{\mathrm{1}+\mu^{\mathrm{2}} }+{C} \\ $$$${e}^{\mu\theta} {T}=\frac{\lambda{gRe}^{\mu\theta} \left\{\mathrm{2}\mu\:\mathrm{cos}\:\theta+\left(\mathrm{1}−\mu^{\mathrm{2}} \right)\mathrm{sin}\:\theta\right\}}{\mathrm{1}+\mu^{\mathrm{2}} }+{C} \\ $$$$\Rightarrow{T}=\frac{\lambda{gR}\left\{\mathrm{2}\mu\:\mathrm{cos}\:\theta+\left(\mathrm{1}−\mu^{\mathrm{2}} \right)\mathrm{sin}\:\theta\right\}}{\mathrm{1}+\mu^{\mathrm{2}} }+{Ce}^{−\mu\theta} \\ $$$${at}\:\theta=\mathrm{0}:\:{T}=\mathrm{0} \\ $$$$\frac{\mathrm{2}\lambda{gR}\mu}{\mathrm{1}+\mu^{\mathrm{2}} }+{C}=\mathrm{0} \\ $$$${C}=−\frac{\mathrm{2}\lambda{gR}\mu}{\mathrm{1}+\mu^{\mathrm{2}} } \\ $$$$\Rightarrow{T}=\frac{\lambda{gR}}{\mathrm{1}+\mu^{\mathrm{2}} }\left[\left(\mathrm{1}−\mu^{\mathrm{2}} \right)\:\mathrm{sin}\:\theta+\mathrm{2}\mu\left(\mathrm{cos}\:\theta−{e}^{−\mu\theta} \right)\right] \\ $$$${the}\:{friction}\:{coeifficient}\:{is}\:{big}\:{enough} \\ $$$${if}\:{no}\:{tension}\:{force}\:{is}\:{needed}\:{to}\:{hold} \\ $$$${the}\:{rope}\:{at}\:{its}\:{topmost}\:{point}. \\ $$$${at}\:\theta=\frac{\pi}{\mathrm{2}}:\:{T}\overset{!} {=}\mathrm{0} \\ $$$$\frac{\lambda{gR}}{\mathrm{1}+\mu^{\mathrm{2}} }\left(\mathrm{1}−\mu^{\mathrm{2}} −\mathrm{2}\mu{e}^{−\frac{\mu\pi}{\mathrm{2}}} \right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{1}−\mu^{\mathrm{2}} −\mathrm{2}\mu{e}^{−\frac{\mu\pi}{\mathrm{2}}} =\mathrm{0} \\ $$$$\Rightarrow\mu\approx\mathrm{0}.\mathrm{7324} \\ $$$$\left[{Option}\:{B}\:{gives}\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}=\mathrm{0}.\mathrm{707}\right] \\ $$$$ \\ $$$$\frac{{dT}}{{d}\theta}=…\left[\left(\mathrm{1}−\mu^{\mathrm{2}} \right)\mathrm{cos}\:\theta+\mathrm{2}\mu\left(−\mathrm{sin}\:\theta+\mu{e}^{−\mu\theta} \right)\right]=\mathrm{0} \\ $$$$\Rightarrow\frac{\mathrm{sin}\:\theta−\mu{e}^{−\mu\theta} }{\mathrm{cos}\:\theta}=\frac{\mathrm{1}−\mu^{\mathrm{2}} }{\mathrm{2}\mu} \\ $$$$\Rightarrow\theta\:{in}\:{terms}\:{of}\:\mu \\ $$$$ \\ $$$${with}\:\mu=\mathrm{0}.\mathrm{7324}\Rightarrow\theta=\mathrm{41}.\mathrm{74}° \\ $$$$\Rightarrow{T}_{{max}} =\mathrm{0}.\mathrm{353}\lambda{Rg} \\ $$$$\left[{Option}\:{D}\:{gives}\:\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\lambda{Rg}=\mathrm{0}.\mathrm{414}\lambda{Rg}\right] \\ $$
Commented by ajfour last updated on 07/Oct/18

$${yes}\:{Sir},\:{true}. \\ $$
Commented by MrW3 last updated on 07/Oct/18

$${If}\:{we}\:{ignore}\:{the}\:{friction}\:{caused}\:{by}\:{the} \\ $$$${tension}\:{force}\:{in}\:{rope},\:{i}.{e}.\:{if}\:{we}\:{ignore} \\ $$$${the}\:{term}\:\mu{T}\:{in}\:{the}\:{eqn}. \\ $$$$\frac{{dT}}{{d}\theta}+\mu{T}=\lambda{gR}\left(\mathrm{cos}\:\theta−\mu\:\mathrm{sin}\:\theta\right), \\ $$$${then}\:{we}\:{will}\:{get} \\ $$$$\frac{{dT}}{{d}\theta}=\lambda{gR}\left(\mathrm{cos}\:\theta−\mu\:\mathrm{sin}\:\theta\right) \\ $$$$\Rightarrow{T}=\lambda{gR}\left(\mathrm{sin}\:\theta+\mu\:\mathrm{cos}\:\theta\right)+{C} \\ $$$${at}\:\theta=\mathrm{0},\:{T}=\mathrm{0}\Rightarrow{C}=−\mu\lambda{Rg} \\ $$$$\Rightarrow{T}=\lambda{gR}\left\{\mathrm{sin}\:\theta+\mu\left(\mathrm{cos}\:\theta−\mathrm{1}\right)\right\} \\ $$$${at}\:\theta=\frac{\pi}{\mathrm{2}},{T}=\mathrm{0}: \\ $$$$\lambda{gR}\left\{\mathrm{1}−\mu\right\}=\mathrm{0}\Rightarrow\mu=\mathrm{1} \\ $$$$ \\ $$$$\frac{{dT}}{{d}\theta}=\lambda{Rg}\left\{\mathrm{cos}\:\theta−\mu\:\mathrm{sin}\:\theta\right\}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{cos}\:\theta−\mu\:\mathrm{sin}\:\theta=\mathrm{0} \\ $$$$\Rightarrow\mathrm{tan}\:\theta=\frac{\mathrm{1}}{\mu}=\mathrm{1}\Rightarrow\theta=\frac{\pi}{\mathrm{4}} \\ $$$${T}_{{max}} =\lambda{Rg}\left\{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}+\mathrm{1}×\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}−\mathrm{1}\right)\right\}=\lambda{Rg}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right) \\ $$$$ \\ $$$${you}\:{see}\:{if}\:{we}\:{ignore}\:{the}\:{friction}\: \\ $$$${caused}\:{by}\:{tension}\:{in}\:{rope},\:{we}\:{will} \\ $$$${get}\:{the}\:{same}\:{result}\:{as}\:{given}\:{in}\:{book}. \\ $$$${but}\:{why}\:{should}\:{we}\:{ignore}\:{it}? \\ $$$${that}'{s}\:{why}\:{I}\:{say}\:{that}\:{the}\:{solution} \\ $$$${given}\:{in}\:{book}\:{is}\:{not}\:{correct}\:\left({enough}\right). \\ $$$$ \\ $$$${certainly},\:{as}\:{we}\:{can}\:{see},\:{ignoring}\:{that} \\ $$$${term}\:{makes}\:{the}\:{solution}\:{much}\:{easier} \\ $$$${than}\:{considering}\:{that}\:{term}. \\ $$
Commented by rahul 19 last updated on 07/Oct/18

$${yes}\:{sir}!\:{Definitely}\:{problem}\:{is}\:{not}\:{clear}. \\ $$$$\left.{Now}\:{it}'{s}\:{understoodable}\::\right) \\ $$
Commented by MrW3 last updated on 07/Oct/18
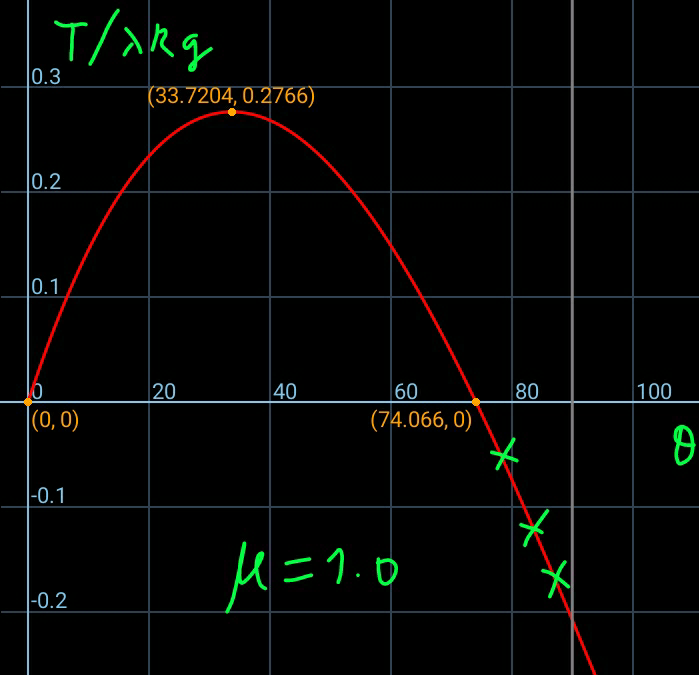
Commented by MrW3 last updated on 07/Oct/18

$${Diagram}\:{above}\:{shows}\:{the}\:{case}\:\mu=\mathrm{1}. \\ $$$${Upon}\:\theta=\mathrm{74}°\:{the}\:{tension}\:{in}\:{rope}\:{is}\:{zero}. \\ $$$${The}\:{maximal}\:{tension}\:{in}\:{rope}\:{is} \\ $$$$\mathrm{0}.\mathrm{28}\lambda{Rg}\:{which}\:{occurs}\:{at}\:\theta=\mathrm{33}.\mathrm{7}°. \\ $$
Commented by MrW3 last updated on 07/Oct/18

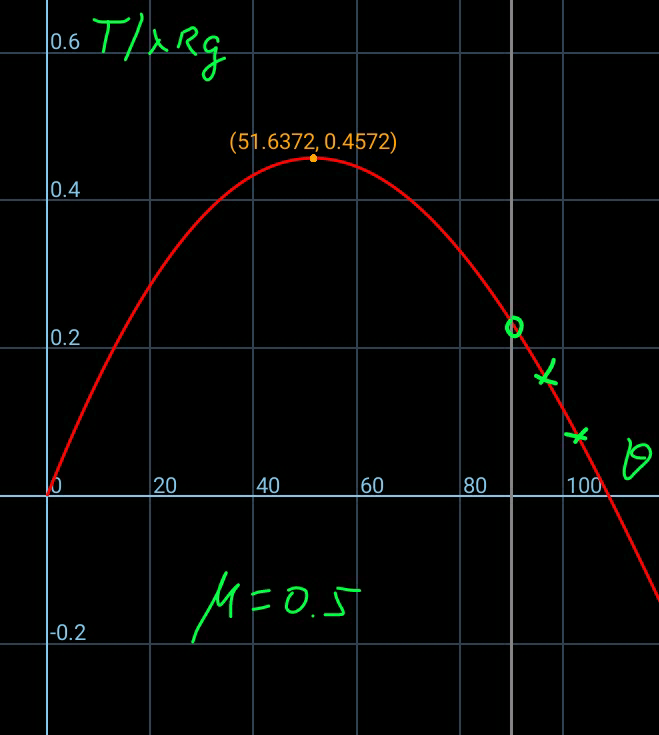
$${This}\:{diagram}\:{shows}\:{the}\:{case}\:\mu=\mathrm{0}.\mathrm{5}. \\ $$$${To}\:{keep}\:{the}\:{rope}\:{from}\:{sliding},\:{a}\:{tension} \\ $$$${force}\:{of}\:\mathrm{0}.\mathrm{23}\lambda{Rg}\:{is}\:{needed}\:{to}\:{hold}\:{the} \\ $$$${rope}\:{at}\:{its}\:{topmost}\:{point}. \\ $$$${The}\:{max}.\:{tension}\:{in}\:{rope}\:{is}\:\mathrm{0}.\mathrm{457}\lambda{Rg} \\ $$$${which}\:{occurs}\:{at}\:\theta=\mathrm{51}.\mathrm{6}°. \\ $$
