Question Number 45019 by rahul 19 last updated on 07/Oct/18
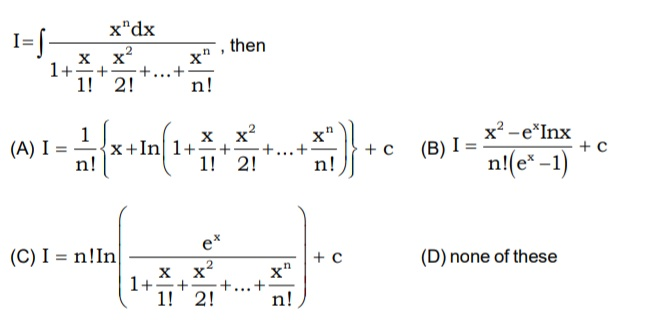
Answered by tanmay.chaudhury50@gmail.com last updated on 08/Oct/18
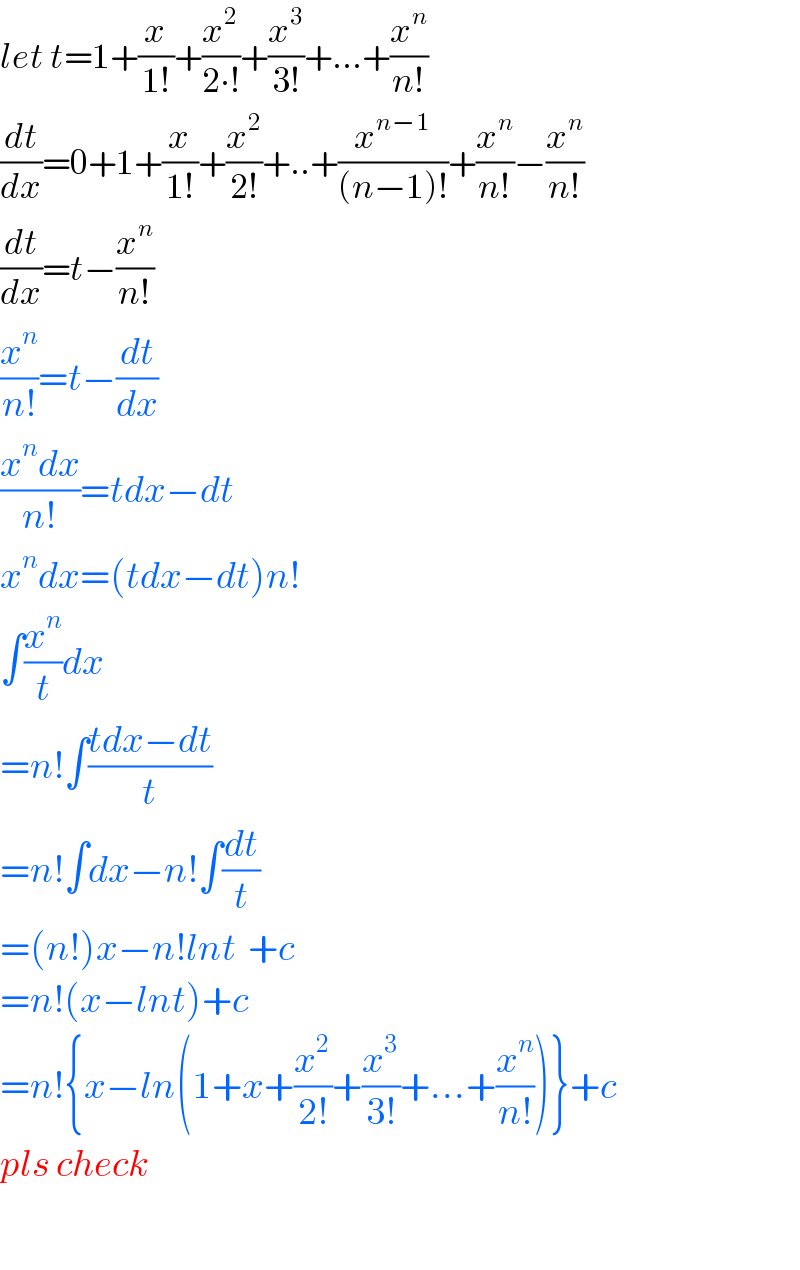
$${let}\:{t}=\mathrm{1}+\frac{{x}}{\mathrm{1}!}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}\centerdot!}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}+…+\frac{{x}^{{n}} }{{n}!} \\ $$$$\frac{{dt}}{{dx}}=\mathrm{0}+\mathrm{1}+\frac{{x}}{\mathrm{1}!}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+..+\frac{{x}^{{n}−\mathrm{1}} }{\left({n}−\mathrm{1}\right)!}+\frac{{x}^{{n}} }{{n}!}−\frac{{x}^{{n}} }{{n}!} \\ $$$$\frac{{dt}}{{dx}}={t}−\frac{{x}^{{n}} }{{n}!} \\ $$$$\frac{{x}^{{n}} }{{n}!}={t}−\frac{{dt}}{{dx}} \\ $$$$\frac{{x}^{{n}} {dx}}{{n}!}={tdx}−{dt} \\ $$$${x}^{{n}} {dx}=\left({tdx}−{dt}\right){n}! \\ $$$$\int\frac{{x}^{{n}} }{{t}}{dx} \\ $$$$={n}!\int\frac{{tdx}−{dt}}{{t}} \\ $$$$={n}!\int{dx}−{n}!\int\frac{{dt}}{{t}} \\ $$$$=\left({n}!\right){x}−{n}!{lnt}\:\:+{c} \\ $$$$={n}!\left({x}−{lnt}\right)+{c} \\ $$$$={n}!\left\{{x}−{ln}\left(\mathrm{1}+{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}+…+\frac{{x}^{{n}} }{{n}!}\right)\right\}+{c} \\ $$$${pls}\:{check}\:\: \\ $$$$ \\ $$
Commented by rahul 19 last updated on 08/Oct/18
thank you so much sir ! ☺️��
Your ans. is correct i.e Option C.
Commented by rahul 19 last updated on 08/Oct/18

$${How}\:{this}\:{method}\:{strike}\:{your}\:{mind}? \\ $$$${I}\:{was}\:{searching}\:{for}\:{some}\:{substitution} \\ $$$${like}\:{in}\:{denominator}\:{i}\:{thought}\:{it}\:{is} \\ $$$${expansion}\:{of}\:{e}^{{x}} . \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 08/Oct/18

$${i}\:{started}\:{this}\:{problem}\:{at}\:\mathrm{1}−\mathrm{30}\:{at}\:{night}…{at}\:{firdt} \\ $$$${i}\:{found}\:{both}\:{function}\:{in}\:{terms}\:{of}\:{t}\:{and}\:{x}… \\ $$$${but}\:{when}\:{placed}\:{in}\:{intregal}\:…{it}\:{got}\:{separated}… \\ $$
