Question Number 45067 by peter frank last updated on 08/Oct/18

Commented by peter frank last updated on 08/Oct/18

$$\mathrm{QN}\:\mathrm{10}\:\mathrm{a} \\ $$
Commented by Tawa1 last updated on 14/Oct/18

$$. \\ $$
Answered by MJS last updated on 08/Oct/18
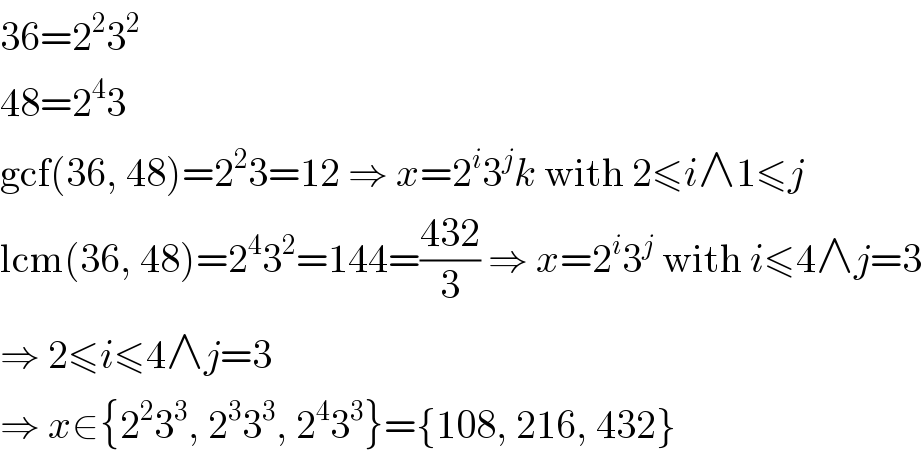
$$\mathrm{36}=\mathrm{2}^{\mathrm{2}} \mathrm{3}^{\mathrm{2}} \\ $$$$\mathrm{48}=\mathrm{2}^{\mathrm{4}} \mathrm{3} \\ $$$$\mathrm{gcf}\left(\mathrm{36},\:\mathrm{48}\right)=\mathrm{2}^{\mathrm{2}} \mathrm{3}=\mathrm{12}\:\Rightarrow\:{x}=\mathrm{2}^{{i}} \mathrm{3}^{{j}} {k}\:\mathrm{with}\:\mathrm{2}\leqslant{i}\wedge\mathrm{1}\leqslant{j}\: \\ $$$$\mathrm{lcm}\left(\mathrm{36},\:\mathrm{48}\right)=\mathrm{2}^{\mathrm{4}} \mathrm{3}^{\mathrm{2}} =\mathrm{144}=\frac{\mathrm{432}}{\mathrm{3}}\:\Rightarrow\:{x}=\mathrm{2}^{{i}} \mathrm{3}^{{j}} \:\mathrm{with}\:{i}\leqslant\mathrm{4}\wedge{j}=\mathrm{3} \\ $$$$\Rightarrow\:\mathrm{2}\leqslant{i}\leqslant\mathrm{4}\wedge{j}=\mathrm{3} \\ $$$$\Rightarrow\:{x}\in\left\{\mathrm{2}^{\mathrm{2}} \mathrm{3}^{\mathrm{3}} ,\:\mathrm{2}^{\mathrm{3}} \mathrm{3}^{\mathrm{3}} ,\:\mathrm{2}^{\mathrm{4}} \mathrm{3}^{\mathrm{3}} \right\}=\left\{\mathrm{108},\:\mathrm{216},\:\mathrm{432}\right\} \\ $$
