Question Number 45125 by Necxx last updated on 09/Oct/18
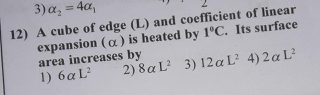
Answered by tanmay.chaudhury50@gmail.com last updated on 09/Oct/18

$${at}\:{temparature}\:{T}\:\:{cube}\:{edge}={L} \\ $$$${at}\:{temp}\:{T}+{dT}\:\:{cube}\:{edge}={L}+{dL} \\ $$$${surface}\:{area}\:{at}\:{tepm}\:{T}\:\:{is}\:{L}^{\mathrm{2}} \\ $$$${at}\:{temp}\:{T}+{dT}\:{surface}\:{area}=\left({L}+{dL}\right)^{\mathrm{2}} \\ $$$${given}\:\alpha=\frac{{dL}}{{L}×{dT}}\:\:\:\:\:\:\:{dL}=\alpha{LdT} \\ $$$${A}={L}^{\mathrm{2}} \:\: \\ $$$${A}+{dA}=\left({L}+{dL}\right)^{\mathrm{2}} ={L}^{\mathrm{2}} +\mathrm{2}{LdL}+\left({dL}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{A}+{dA}\approx{L}^{\mathrm{2}} +\mathrm{2}{LdL} \\ $$$${dA}=\mathrm{2}{LdL} \\ $$$${dA}=\mathrm{2}{L}×\alpha{LdT}=\mathrm{2}\alpha{L}^{\mathrm{2}} {dT} \\ $$$$ \\ $$$${here}\:\:{dT}=\mathrm{1} \\ $$$${so}\:{dA}=\mathrm{2}\alpha{L}^{\mathrm{2}} \\ $$$$ \\ $$$$\bigstar\bigstar\bigstar{for}\:{total}\:{surface}\:{area}… \\ $$$${S}=\mathrm{6}{L}^{\mathrm{2}} \\ $$$${S}+{dS}=\mathrm{6}\left({L}+{dL}\right)^{\mathrm{2}} \approx\mathrm{6}\left({L}^{\mathrm{2}} +\mathrm{2}{LdL}\right) \\ $$$${dS}=\mathrm{12}{LdL} \\ $$$${dS}=\mathrm{12}{L}×\alpha{LdT}=\mathrm{12}\alpha{L}^{\mathrm{2}} {dT} \\ $$$${here}\:{dT}=\mathrm{1} \\ $$$${dS}=\mathrm{12}\alpha{L}^{\mathrm{2}} \\ $$
