Question Number 45128 by Necxx last updated on 09/Oct/18

Commented by Necxx last updated on 09/Oct/18
$${please}\:{help}\:{with}\:{the}\:{last}\:{question}_{} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 09/Oct/18
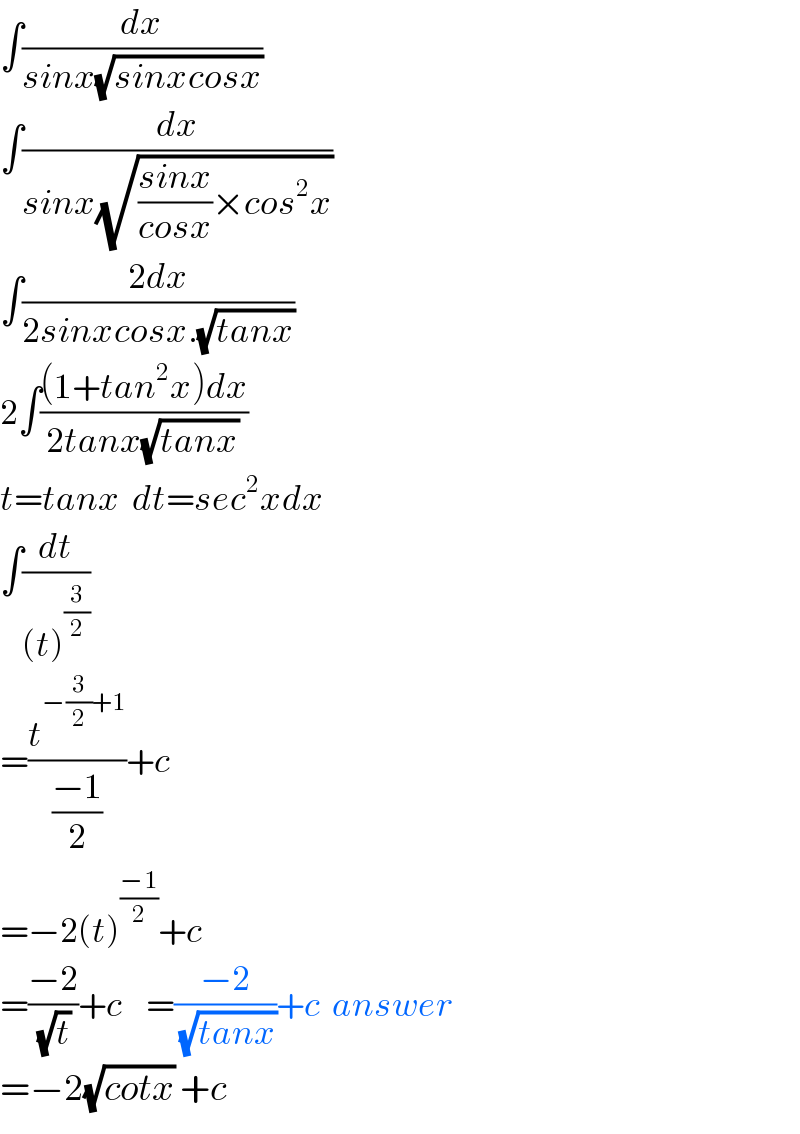
$$\int\frac{{dx}}{{sinx}\sqrt{{sinxcosx}}} \\ $$$$\int\frac{{dx}}{{sinx}\sqrt{\frac{{sinx}}{{cosx}}×{cos}^{\mathrm{2}} {x}}} \\ $$$$\int\frac{\mathrm{2}{dx}}{\mathrm{2}{sinxcosx}.\sqrt{{tanx}}} \\ $$$$\mathrm{2}\int\frac{\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right){dx}}{\mathrm{2}{tanx}\sqrt{{tanx}}} \\ $$$${t}={tanx}\:\:{dt}={sec}^{\mathrm{2}} {xdx} \\ $$$$\int\frac{{dt}}{\left({t}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$$=\frac{{t}^{−\frac{\mathrm{3}}{\mathrm{2}}+\mathrm{1}} }{\frac{−\mathrm{1}}{\mathrm{2}}}+{c} \\ $$$$=−\mathrm{2}\left({t}\right)^{\frac{−\mathrm{1}}{\mathrm{2}}} +{c} \\ $$$$=\frac{−\mathrm{2}}{\:\sqrt{{t}}}+{c}\:\:\:\:=\frac{−\mathrm{2}}{\:\sqrt{{tanx}}}+{c}\:\:{answer} \\ $$$$=−\mathrm{2}\sqrt{{cotx}}\:+{c} \\ $$
Commented by Necxx last updated on 09/Oct/18
$${wow}….{I}\:{love}\:{this}..{Thank}\:{you}\:{so} \\ $$$${much}_{} \\ $$
