Menu Close

Question-45187

Tinku Tara 0 Comments
Pin




Question Number 45187 by MrW3 last updated on 10/Oct/18
Commented by MrW3 last updated on 12/Oct/18
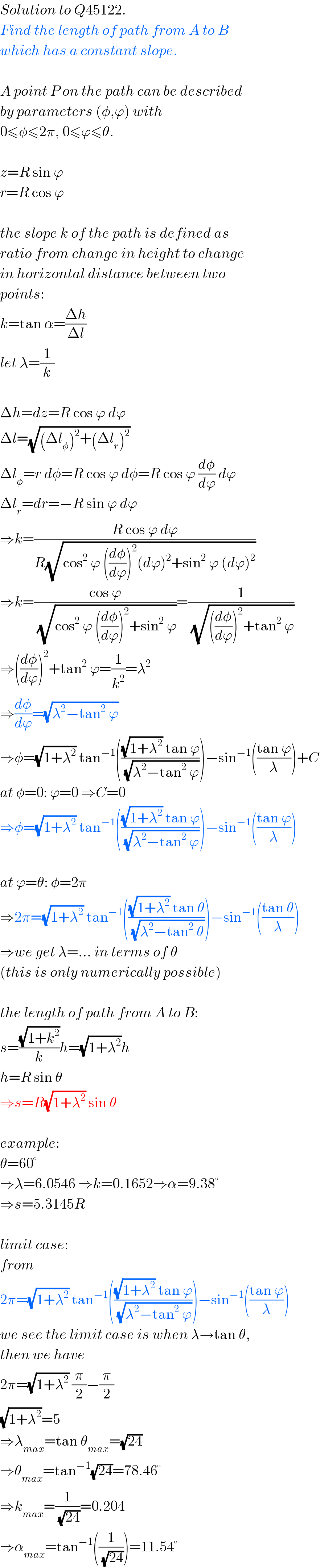
Solution to Q45122. Find the length of path from A to B which has a constant slope. A point P on the path can be described by parameters (φ,ϕ) with 0≤φ≤2π, 0≤ϕ≤θ. z=R sin ϕ r=R cos ϕ the slope k of the path is defined as ratio from change in height to change in horizontal distance between two points: k=tan α=((Δh)/(Δl)) let λ=(1/k) Δh=dz=R cos ϕ dϕ Δl=(√((Δl_φ )^2 +(Δl_r )^2 )) Δl_φ =r dφ=R cos ϕ dφ=R cos ϕ (dφ/dϕ) dϕ Δl_r =dr=−R sin ϕ dϕ ⇒k=((R cos ϕ dϕ)/(R(√(cos^2 ϕ ((dφ/dϕ))^2 (dϕ)^2 +sin^2 ϕ (dϕ)^2 )))) ⇒k=((cos ϕ)/( (√(cos^2 ϕ ((dφ/dϕ))^2 +sin^2 ϕ))))=(1/( (√(((dφ/dϕ))^2 +tan^2 ϕ)))) ⇒((dφ/dϕ))^2 +tan^2 ϕ=(1/k^2 )=λ^2 ⇒(dφ/dϕ)=(√(λ^2 −tan^2 ϕ)) ⇒φ=(√(1+λ^2 )) tan^(−1) ((((√(1+λ^2 )) tan ϕ)/( (√(λ^2 −tan^2 ϕ)))))−sin^(−1) (((tan ϕ)/λ))+C at φ=0: ϕ=0 ⇒C=0 ⇒φ=(√(1+λ^2 )) tan^(−1) ((((√(1+λ^2 )) tan ϕ)/( (√(λ^2 −tan^2 ϕ)))))−sin^(−1) (((tan ϕ)/λ)) at ϕ=θ: φ=2π ⇒2π=(√(1+λ^2 )) tan^(−1) ((((√(1+λ^2 )) tan θ)/( (√(λ^2 −tan^2 θ)))))−sin^(−1) (((tan θ)/λ)) ⇒we get λ=... in terms of θ (this is only numerically possible) the length of path from A to B: s=((√(1+k^2 ))/k)h=(√(1+λ^2 ))h h=R sin θ ⇒s=R(√(1+λ^2 )) sin θ example: θ=60° ⇒λ=6.0546 ⇒k=0.1652⇒α=9.38° ⇒s=5.3145R limit case: from 2π=(√(1+λ^2 )) tan^(−1) ((((√(1+λ^2 )) tan ϕ)/( (√(λ^2 −tan^2 ϕ)))))−sin^(−1) (((tan ϕ)/λ)) we see the limit case is when λ→tan θ, then we have 2π=(√(1+λ^2 )) (π/2)−(π/2) (√(1+λ^2 ))=5 ⇒λ_(max) =tan θ_(max) =(√(24)) ⇒θ_(max) =tan^(−1) (√(24))=78.46° ⇒k_(max) =(1/( (√(24))))=0.204 ⇒α_(max) =tan^(−1) ((1/( (√(24)))))=11.54°
$${Solution}\:{to}\:{Q}\mathrm{45122}. \\ $$$${Find}\:{the}\:{length}\:{of}\:{path}\:{from}\:{A}\:{to}\:{B} \\ $$$${which}\:{has}\:{a}\:{constant}\:{slope}. \\ $$$$ \\ $$$${A}\:{point}\:{P}\:{on}\:{the}\:{path}\:{can}\:{be}\:{described} \\ $$$${by}\:{parameters}\:\left(\phi,\varphi\right)\:{with}\: \\ $$$$\mathrm{0}\leqslant\phi\leqslant\mathrm{2}\pi,\:\mathrm{0}\leqslant\varphi\leqslant\theta. \\ $$$$ \\ $$$${z}={R}\:\mathrm{sin}\:\varphi \\ $$$${r}={R}\:\mathrm{cos}\:\varphi \\ $$$$ \\ $$$${the}\:{slope}\:{k}\:{of}\:{the}\:{path}\:{is}\:{defined}\:{as}\: \\ $$$${ratio}\:{from}\:{change}\:{in}\:{height}\:{to}\:{change} \\ $$$${in}\:{horizontal}\:{distance}\:{between}\:{two} \\ $$$${points}: \\ $$$${k}=\mathrm{tan}\:\alpha=\frac{\Delta{h}}{\Delta{l}} \\ $$$${let}\:\lambda=\frac{\mathrm{1}}{{k}} \\ $$$$ \\ $$$$\Delta{h}={dz}={R}\:\mathrm{cos}\:\varphi\:{d}\varphi \\ $$$$\Delta{l}=\sqrt{\left(\Delta{l}_{\phi} \right)^{\mathrm{2}} +\left(\Delta{l}_{{r}} \right)^{\mathrm{2}} } \\ $$$$\Delta{l}_{\phi} ={r}\:{d}\phi={R}\:\mathrm{cos}\:\varphi\:{d}\phi={R}\:\mathrm{cos}\:\varphi\:\frac{{d}\phi}{{d}\varphi}\:{d}\varphi \\ $$$$\Delta{l}_{{r}} ={dr}=−{R}\:\mathrm{sin}\:\varphi\:{d}\varphi \\ $$$$\Rightarrow{k}=\frac{{R}\:\mathrm{cos}\:\varphi\:{d}\varphi}{{R}\sqrt{\mathrm{cos}^{\mathrm{2}} \:\varphi\:\left(\frac{{d}\phi}{{d}\varphi}\right)^{\mathrm{2}} \left({d}\varphi\right)^{\mathrm{2}} +\mathrm{sin}^{\mathrm{2}} \:\varphi\:\left({d}\varphi\right)^{\mathrm{2}} }} \\ $$$$\Rightarrow{k}=\frac{\mathrm{cos}\:\varphi}{\:\sqrt{\mathrm{cos}^{\mathrm{2}} \:\varphi\:\left(\frac{{d}\phi}{{d}\varphi}\right)^{\mathrm{2}} +\mathrm{sin}^{\mathrm{2}} \:\varphi}}=\frac{\mathrm{1}}{\:\sqrt{\left(\frac{{d}\phi}{{d}\varphi}\right)^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\varphi}} \\ $$$$\Rightarrow\left(\frac{{d}\phi}{{d}\varphi}\right)^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\varphi=\frac{\mathrm{1}}{{k}^{\mathrm{2}} }=\lambda^{\mathrm{2}} \\ $$$$\Rightarrow\frac{{d}\phi}{{d}\varphi}=\sqrt{\lambda^{\mathrm{2}} −\mathrm{tan}^{\mathrm{2}} \:\varphi} \\ $$$$\Rightarrow\phi=\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }\:\mathrm{tan}\:\varphi}{\:\sqrt{\lambda^{\mathrm{2}} −\mathrm{tan}^{\mathrm{2}} \:\varphi}}\right)−\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{tan}\:\varphi}{\lambda}\right)+{C} \\ $$$${at}\:\phi=\mathrm{0}:\:\varphi=\mathrm{0}\:\Rightarrow{C}=\mathrm{0} \\ $$$$\Rightarrow\phi=\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }\:\mathrm{tan}\:\varphi}{\:\sqrt{\lambda^{\mathrm{2}} −\mathrm{tan}^{\mathrm{2}} \:\varphi}}\right)−\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{tan}\:\varphi}{\lambda}\right) \\ $$$$ \\ $$$${at}\:\varphi=\theta:\:\phi=\mathrm{2}\pi \\ $$$$\Rightarrow\mathrm{2}\pi=\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }\:\mathrm{tan}\:\theta}{\:\sqrt{\lambda^{\mathrm{2}} −\mathrm{tan}^{\mathrm{2}} \:\theta}}\right)−\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{tan}\:\theta}{\lambda}\right) \\ $$$$\Rightarrow{we}\:{get}\:\lambda=…\:{in}\:{terms}\:{of}\:\theta \\ $$$$\left({this}\:{is}\:{only}\:{numerically}\:{possible}\right) \\ $$$$ \\ $$$${the}\:{length}\:{of}\:{path}\:{from}\:{A}\:{to}\:{B}: \\ $$$${s}=\frac{\sqrt{\mathrm{1}+{k}^{\mathrm{2}} }}{{k}}{h}=\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }{h} \\ $$$${h}={R}\:\mathrm{sin}\:\theta \\ $$$$\Rightarrow{s}={R}\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }\:\mathrm{sin}\:\theta \\ $$$$ \\ $$$${example}: \\ $$$$\theta=\mathrm{60}° \\ $$$$\Rightarrow\lambda=\mathrm{6}.\mathrm{0546}\:\Rightarrow{k}=\mathrm{0}.\mathrm{1652}\Rightarrow\alpha=\mathrm{9}.\mathrm{38}° \\ $$$$\Rightarrow{s}=\mathrm{5}.\mathrm{3145}{R} \\ $$$$ \\ $$$${limit}\:{case}: \\ $$$${from} \\ $$$$\mathrm{2}\pi=\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }\:\mathrm{tan}\:\varphi}{\:\sqrt{\lambda^{\mathrm{2}} −\mathrm{tan}^{\mathrm{2}} \:\varphi}}\right)−\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{tan}\:\varphi}{\lambda}\right) \\ $$$${we}\:{see}\:{the}\:{limit}\:{case}\:{is}\:{when}\:\lambda\rightarrow\mathrm{tan}\:\theta, \\ $$$${then}\:{we}\:{have} \\ $$$$\mathrm{2}\pi=\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }\:\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{2}} \\ $$$$\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }=\mathrm{5} \\ $$$$\Rightarrow\lambda_{{max}} =\mathrm{tan}\:\theta_{{max}} =\sqrt{\mathrm{24}} \\ $$$$\Rightarrow\theta_{{max}} =\mathrm{tan}^{−\mathrm{1}} \sqrt{\mathrm{24}}=\mathrm{78}.\mathrm{46}° \\ $$$$\Rightarrow{k}_{{max}} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{24}}}=\mathrm{0}.\mathrm{204} \\ $$$$\Rightarrow\alpha_{{max}} =\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{24}}}\right)=\mathrm{11}.\mathrm{54}° \\ $$
Commented by MJS last updated on 10/Oct/18
great! another aspect (sorry if it seems I′m always looking for problems, borders or mistakes, but I′m really interested) you cannot reach some regions above a certain θ within a turn of 2π because the slope is limited by the slope of the sphere. Can we find the maximum θ for this case?
$$\mathrm{great}! \\ $$$$\mathrm{another}\:\mathrm{aspect}\:\left(\mathrm{sorry}\:\mathrm{if}\:\mathrm{it}\:\mathrm{seems}\:\mathrm{I}'\mathrm{m}\:\mathrm{always}\right. \\ $$$$\mathrm{looking}\:\mathrm{for}\:\mathrm{problems},\:\mathrm{borders}\:\mathrm{or}\:\mathrm{mistakes}, \\ $$$$\left.\mathrm{but}\:\mathrm{I}'\mathrm{m}\:\mathrm{really}\:\mathrm{interested}\right) \\ $$$$\mathrm{you}\:\mathrm{cannot}\:\mathrm{reach}\:\mathrm{some}\:\mathrm{regions}\:\mathrm{above}\:\mathrm{a}\:\mathrm{certain} \\ $$$$\theta\:\mathrm{within}\:\mathrm{a}\:\mathrm{turn}\:\mathrm{of}\:\mathrm{2}\pi\:\mathrm{because}\:\mathrm{the}\:\mathrm{slope}\:\mathrm{is} \\ $$$$\mathrm{limited}\:\mathrm{by}\:\mathrm{the}\:\mathrm{slope}\:\mathrm{of}\:\mathrm{the}\:\mathrm{sphere}. \\ $$$$\mathrm{Can}\:\mathrm{we}\:\mathrm{find}\:\mathrm{the}\:\mathrm{maximum}\:\theta\:\mathrm{for}\:\mathrm{this}\:\mathrm{case}? \\ $$
Commented by ajfour last updated on 10/Oct/18
Wonderful analysis Sir, but how was the integration done Sir ? ∫_0 ^( θ) (√(λ^2 −tan^2 ϕ)) dϕ
$${Wonderful}\:{analysis}\:{Sir},\: \\ $$$${but}\:{how}\:{was}\:{the}\:{integration}\:{done} \\ $$$${Sir}\:? \\ $$$$\:\:\int_{\mathrm{0}} ^{\:\:\theta} \sqrt{\lambda^{\mathrm{2}} −\mathrm{tan}\:^{\mathrm{2}} \varphi}\:{d}\varphi\:\: \\ $$
Commented by MJS last updated on 10/Oct/18
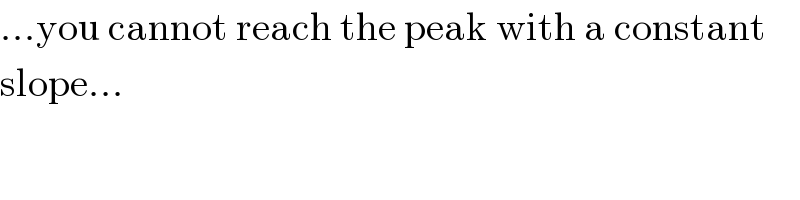
...you cannot reach the peak with a constant slope...
$$…\mathrm{you}\:\mathrm{cannot}\:\mathrm{reach}\:\mathrm{the}\:\mathrm{peak}\:\mathrm{with}\:\mathrm{a}\:\mathrm{constant} \\ $$$$\mathrm{slope}… \\ $$
Commented by MrW3 last updated on 10/Oct/18
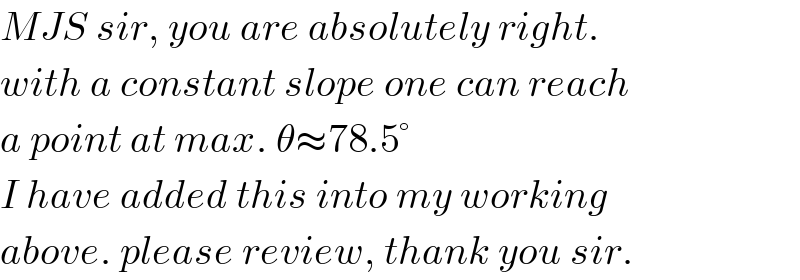
MJS sir, you are absolutely right. with a constant slope one can reach a point at max. θ≈78.5° I have added this into my working above. please review, thank you sir.
$${MJS}\:{sir},\:{you}\:{are}\:{absolutely}\:{right}. \\ $$$${with}\:{a}\:{constant}\:{slope}\:{one}\:{can}\:{reach} \\ $$$${a}\:{point}\:{at}\:{max}.\:\theta\approx\mathrm{78}.\mathrm{5}° \\ $$$${I}\:{have}\:{added}\:{this}\:{into}\:{my}\:{working} \\ $$$${above}.\:{please}\:{review},\:{thank}\:{you}\:{sir}. \\ $$
Commented by MrW3 last updated on 10/Oct/18
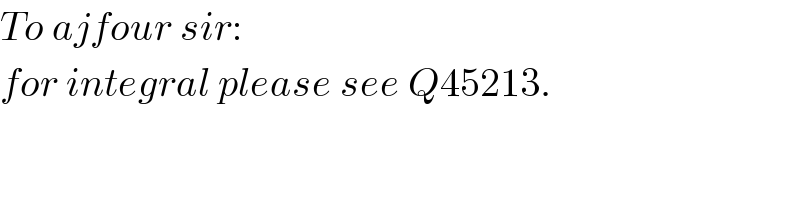
To ajfour sir: for integral please see Q45213.
$${To}\:{ajfour}\:{sir}: \\ $$$${for}\:{integral}\:{please}\:{see}\:{Q}\mathrm{45213}. \\ $$
Answered by ajitbh last updated on 10/Oct/18
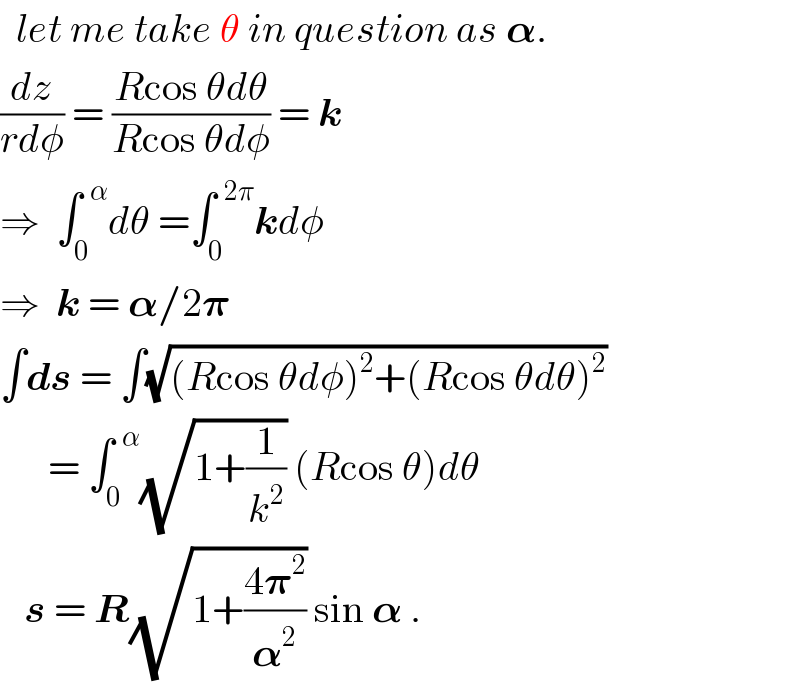
let me take θ in question as 𝛂. (dz/(rdφ)) = ((Rcos θdθ)/(Rcos θdφ)) = k ⇒ ∫_0 ^( α) dθ =∫_0 ^( 2π) kdφ ⇒ k = 𝛂/2𝛑 ∫ds = ∫(√((Rcos θdφ)^2 +(Rcos θdθ)^2 )) = ∫_0 ^( α) (√(1+(1/k^2 ))) (Rcos θ)dθ s = R(√(1+((4𝛑^2 )/𝛂^2 ))) sin 𝛂 .
$$\:\:{let}\:{me}\:{take}\:\theta\:{in}\:{question}\:{as}\:\boldsymbol{\alpha}. \\ $$$$\frac{{dz}}{{rd}\phi}\:=\:\frac{{R}\mathrm{cos}\:\theta{d}\theta}{{R}\mathrm{cos}\:\theta{d}\phi}\:=\:\boldsymbol{{k}} \\ $$$$\Rightarrow\:\:\int_{\mathrm{0}} ^{\:\:\alpha} {d}\theta\:=\int_{\mathrm{0}} ^{\:\:\mathrm{2}\pi} \boldsymbol{{k}}{d}\phi \\ $$$$\Rightarrow\:\:\boldsymbol{{k}}\:=\:\boldsymbol{\alpha}/\mathrm{2}\boldsymbol{\pi} \\ $$$$\int\boldsymbol{{ds}}\:=\:\int\sqrt{\left({R}\mathrm{cos}\:\theta{d}\phi\right)^{\mathrm{2}} +\left({R}\mathrm{cos}\:\theta{d}\theta\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:=\:\int_{\mathrm{0}} ^{\:\:\alpha} \sqrt{\mathrm{1}+\frac{\mathrm{1}}{{k}^{\mathrm{2}} }}\:\left({R}\mathrm{cos}\:\theta\right){d}\theta \\ $$$$\:\:\:\boldsymbol{{s}}\:=\:\boldsymbol{{R}}\sqrt{\mathrm{1}+\frac{\mathrm{4}\boldsymbol{\pi}^{\mathrm{2}} }{\boldsymbol{\alpha}^{\mathrm{2}} }}\:\mathrm{sin}\:\boldsymbol{\alpha}\:. \\ $$
Commented by ajitbh last updated on 10/Oct/18
Sir, my tinkutara app is crashing i changed id, yet the problem persists..
$${Sir},\:{my}\:{tinkutara}\:{app}\:{is}\:{crashing} \\ $$$${i}\:{changed}\:{id},\:{yet}\:{the}\:{problem} \\ $$$${persists}.. \\ $$
Commented by MrW3 last updated on 10/Oct/18
sir, I see, hope the app problem will be solved soon.
$${sir},\:{I}\:{see},\:{hope}\:{the}\:{app}\:{problem}\:{will}\:{be} \\ $$$${solved}\:{soon}. \\ $$
Commented by MrW3 last updated on 10/Oct/18
one question to your solution: in (dz/(rdφ)) = ((Rcos θdθ)/(Rcos θdφ)) = k you assumed that r is constant. but if r is not constant, as in this case, dl≠rdφ, but dl=(√((rdφ)^2 +(dr)^2 )), as we know from polar coordinate system when calculating length of curve. can you please check sir. thank you.
$${one}\:{question}\:{to}\:{your}\:{solution}: \\ $$$${in}\:\frac{{dz}}{{rd}\phi}\:=\:\frac{{R}\mathrm{cos}\:\theta{d}\theta}{{R}\mathrm{cos}\:\theta{d}\phi}\:=\:\boldsymbol{{k}} \\ $$$${you}\:{assumed}\:{that}\:{r}\:{is}\:{constant}.\:{but} \\ $$$${if}\:{r}\:{is}\:{not}\:{constant},\:{as}\:{in}\:{this}\:{case}, \\ $$$${dl}\neq{rd}\phi,\:{but}\:{dl}=\sqrt{\left({rd}\phi\right)^{\mathrm{2}} +\left({dr}\right)^{\mathrm{2}} },\:{as} \\ $$$${we}\:{know}\:{from}\:{polar}\:{coordinate}\:{system} \\ $$$${when}\:{calculating}\:{length}\:{of}\:{curve}. \\ $$$${can}\:{you}\:{please}\:{check}\:{sir}.\:{thank}\:{you}. \\ $$
Commented by ajfour last updated on 10/Oct/18
checked sir, but the solution cant be deleted very soon..!
$${checked}\:{sir},\:{but}\:{the}\:{solution}\:{cant} \\ $$$${be}\:{deleted}\:{very}\:{soon}..! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *