Menu Close

Question-45205

Tinku Tara 0 Comments
Pin




Question Number 45205 by Necxx last updated on 10/Oct/18
Answered by tanmay.chaudhury50@gmail.com last updated on 11/Oct/18
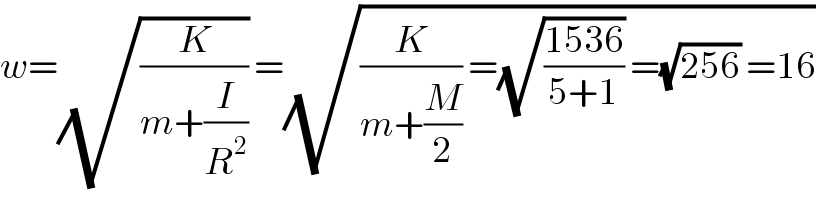
w=(√(K/(m+(I/R^2 )))) =(√((K/(m+(M/2))) =(√((1536)/(5+1))) =(√(256)) =16))
$${w}=\sqrt{\frac{{K}}{{m}+\frac{{I}}{{R}^{\mathrm{2}} }}}\:=\sqrt{\frac{{K}}{{m}+\frac{{M}}{\mathrm{2}}}\:=\sqrt{\frac{\mathrm{1536}}{\mathrm{5}+\mathrm{1}}}\:=\sqrt{\mathrm{256}}\:=\mathrm{16}} \\ $$
Commented by Necxx last updated on 12/Oct/18
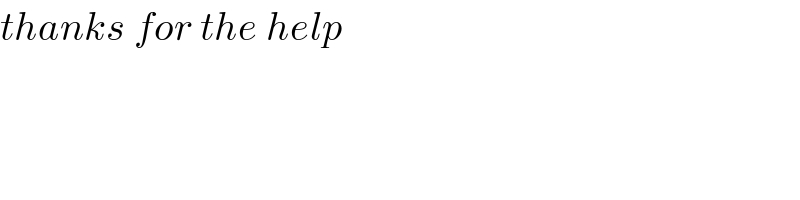
thanks for the help
$${thanks}\:{for}\:{the}\:{help} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 11/Oct/18
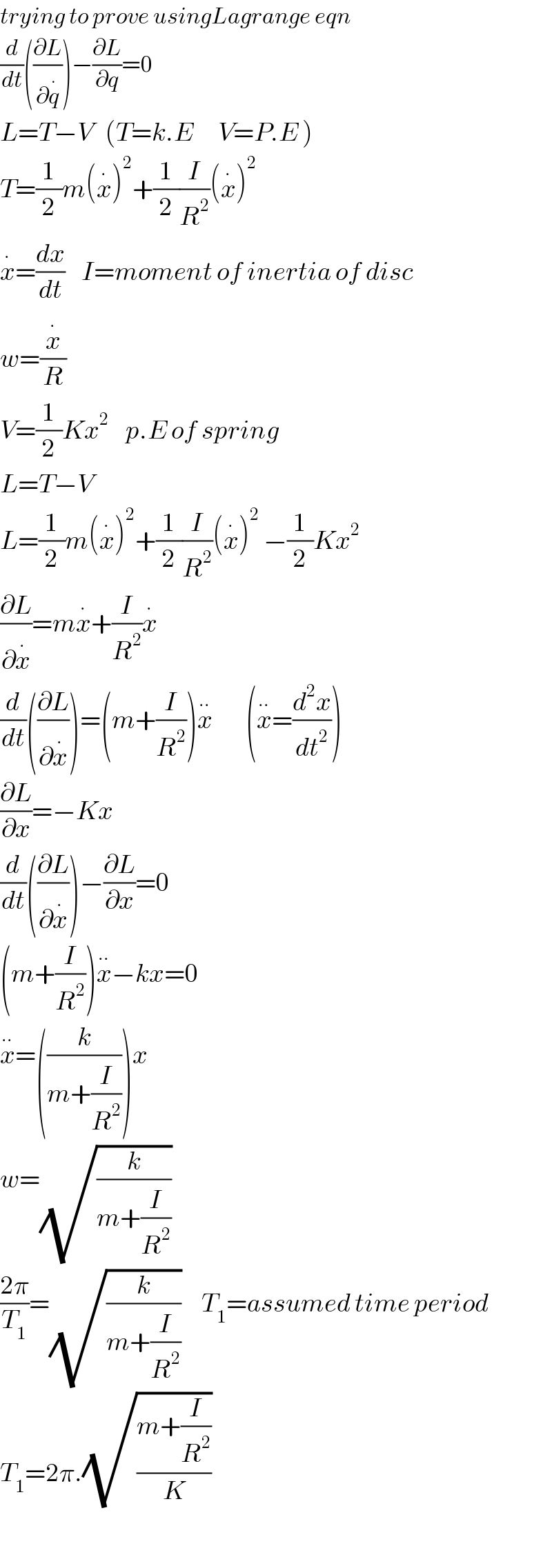
trying to prove usingLagrange eqn (d/dt)((∂L/∂q^. ))−(∂L/∂q)=0 L=T−V (T=k.E V=P.E ) T=(1/2)m(x^. )^2 +(1/2)(I/R^2 )(x^. )^2 x^. =(dx/dt) I=moment of inertia of disc w=(x^. /R) V=(1/2)Kx^2 p.E of spring L=T−V L=(1/2)m(x^. )^2 +(1/2)(I/R^2 )(x^. )^2 −(1/2)Kx^2 (∂L/∂x^. )=mx^. +(I/R^2 )x^. (d/dt)((∂L/∂x^. ))=(m+(I/R^2 ))x^(..) (x^(..) =(d^2 x/dt^2 )) (∂L/∂x)=−Kx (d/dt)((∂L/∂x^. ))−(∂L/∂x)=0 (m+(I/R^2 ))x^(..) −kx=0 x^(..) =((k/(m+(I/R^2 ))))x w=(√(k/(m+(I/R^2 )))) ((2π)/T_1 )=(√(k/(m+(I/R^2 )))) T_1 =assumed time period T_1 =2π.(√((m+(I/R^2 ))/K))
$${trying}\:{to}\:{prove}\:{usingLagrange}\:{eqn} \\ $$$$\frac{{d}}{{dt}}\left(\frac{\partial{L}}{\partial\overset{.} {{q}}}\right)−\frac{\partial{L}}{\partial{q}}=\mathrm{0} \\ $$$${L}={T}−{V}\:\:\:\left({T}={k}.{E}\:\:\:\:\:\:{V}={P}.{E}\:\right) \\ $$$${T}=\frac{\mathrm{1}}{\mathrm{2}}{m}\left(\overset{.} {{x}}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\frac{{I}}{{R}^{\mathrm{2}} }\left(\overset{.} {{x}}\right)^{\mathrm{2}} \\ $$$$\overset{.} {{x}}=\frac{{dx}}{{dt}}\:\:\:\:{I}={moment}\:{of}\:{inertia}\:{of}\:{disc} \\ $$$${w}=\frac{\overset{.} {{x}}}{{R}} \\ $$$${V}=\frac{\mathrm{1}}{\mathrm{2}}{Kx}^{\mathrm{2}} \:\:\:\:{p}.{E}\:{of}\:{spring} \\ $$$${L}={T}−{V} \\ $$$${L}=\frac{\mathrm{1}}{\mathrm{2}}{m}\left(\overset{.} {{x}}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\frac{{I}}{{R}^{\mathrm{2}} }\left(\overset{.} {{x}}\right)^{\mathrm{2}} \:−\frac{\mathrm{1}}{\mathrm{2}}{Kx}^{\mathrm{2}} \\ $$$$\frac{\partial{L}}{\partial\overset{.} {{x}}}={m}\overset{.} {{x}}+\frac{{I}}{{R}^{\mathrm{2}} }\overset{.} {{x}}\:\:\:\: \\ $$$$\frac{{d}}{{dt}}\left(\frac{\partial{L}}{\partial\overset{.} {{x}}}\right)=\left({m}+\frac{{I}}{{R}^{\mathrm{2}} }\right)\overset{..} {{x}}\:\:\:\:\:\:\:\:\left(\overset{..} {{x}}=\frac{{d}^{\mathrm{2}} {x}}{{dt}^{\mathrm{2}} }\right) \\ $$$$\frac{\partial{L}}{\partial{x}}=−{Kx} \\ $$$$\frac{{d}}{{dt}}\left(\frac{\partial{L}}{\partial\overset{.} {{x}}}\right)−\frac{\partial{L}}{\partial{x}}=\mathrm{0} \\ $$$$\left({m}+\frac{{I}}{{R}^{\mathrm{2}} }\right)\overset{..} {{x}}−{kx}=\mathrm{0} \\ $$$$\overset{..} {{x}}=\left(\frac{{k}}{{m}+\frac{{I}}{{R}^{\mathrm{2}} }}\right){x} \\ $$$${w}=\sqrt{\frac{{k}}{{m}+\frac{{I}}{{R}^{\mathrm{2}} }}}\:\: \\ $$$$\frac{\mathrm{2}\pi}{{T}_{\mathrm{1}} }=\sqrt{\frac{{k}}{{m}+\frac{{I}}{{R}^{\mathrm{2}} }}}\:\:\:\:\:{T}_{\mathrm{1}} ={assumed}\:{time}\:{period} \\ $$$${T}_{\mathrm{1}} =\mathrm{2}\pi.\sqrt{\frac{{m}+\frac{{I}}{{R}^{\mathrm{2}} }}{{K}}}\:\: \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *