Question Number 45281 by peter frank last updated on 11/Oct/18
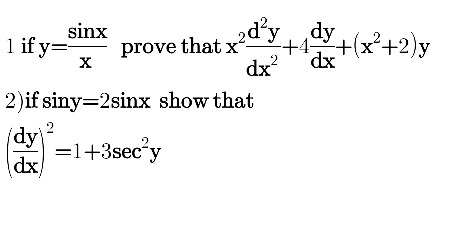
Commented by math1967 last updated on 11/Oct/18

$${pls}\:{chq}.\:{q}.{no}\mathrm{1} \\ $$
Commented by peter frank last updated on 11/Oct/18
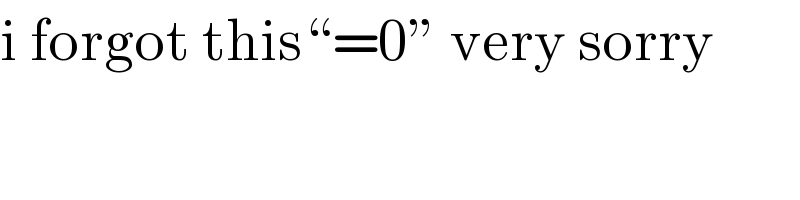
$$\mathrm{i}\:\mathrm{forgot}\:\mathrm{this}“=\mathrm{0}''\:\mathrm{very}\:\mathrm{sorry} \\ $$$$ \\ $$
Answered by math1967 last updated on 11/Oct/18
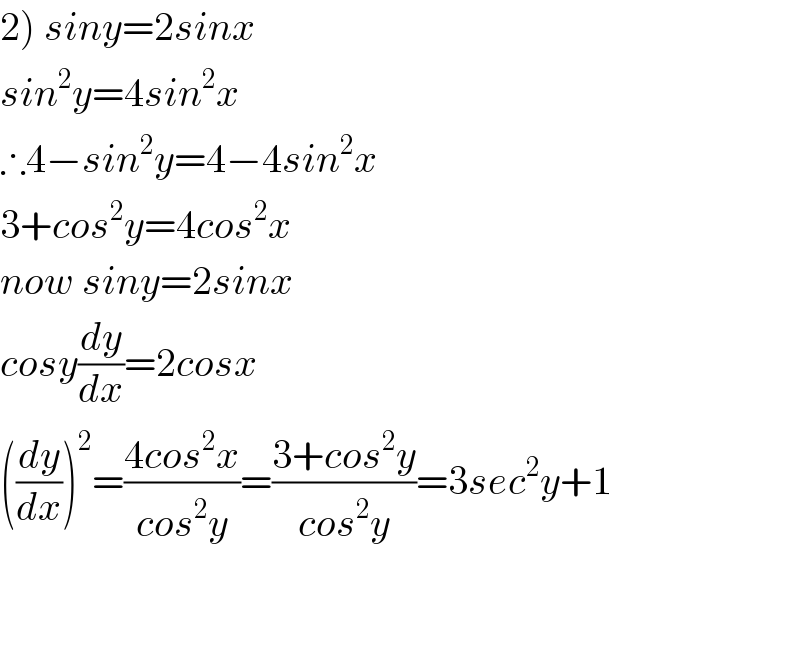
$$\left.\mathrm{2}\right)\:{siny}=\mathrm{2}{sinx} \\ $$$${sin}^{\mathrm{2}} {y}=\mathrm{4}{sin}^{\mathrm{2}} {x} \\ $$$$\therefore\mathrm{4}−{sin}^{\mathrm{2}} {y}=\mathrm{4}−\mathrm{4}{sin}^{\mathrm{2}} {x} \\ $$$$\mathrm{3}+{cos}^{\mathrm{2}} {y}=\mathrm{4}{cos}^{\mathrm{2}} {x} \\ $$$${now}\:{siny}=\mathrm{2}{sinx} \\ $$$${cosy}\frac{{dy}}{{dx}}=\mathrm{2}{cosx} \\ $$$$\left(\frac{{dy}}{{dx}}\right)^{\mathrm{2}} =\frac{\mathrm{4}{cos}^{\mathrm{2}} {x}}{{cos}^{\mathrm{2}} {y}}=\frac{\mathrm{3}+{cos}^{\mathrm{2}} {y}}{{cos}^{\mathrm{2}} {y}}=\mathrm{3}{sec}^{\mathrm{2}} {y}+\mathrm{1} \\ $$$$ \\ $$$$ \\ $$
Commented by peter frank last updated on 11/Oct/18
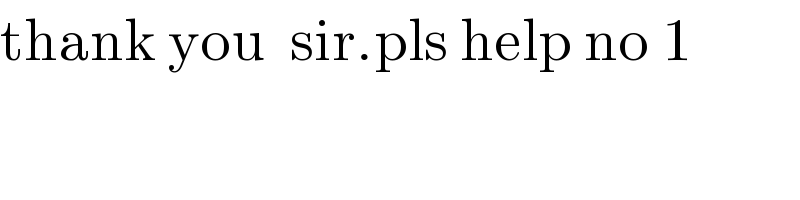
$$\mathrm{thank}\:\mathrm{you}\:\:\mathrm{sir}.\mathrm{pls}\:\mathrm{help}\:\mathrm{no}\:\mathrm{1} \\ $$
