Question Number 45284 by ajfour last updated on 11/Oct/18
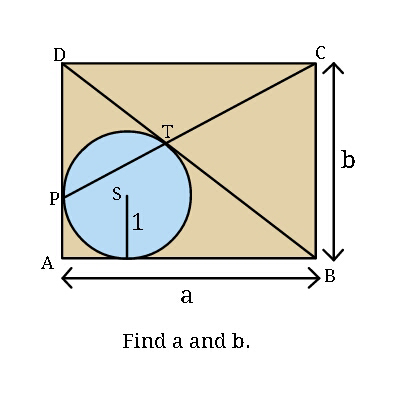
Commented by ajfour last updated on 11/Oct/18
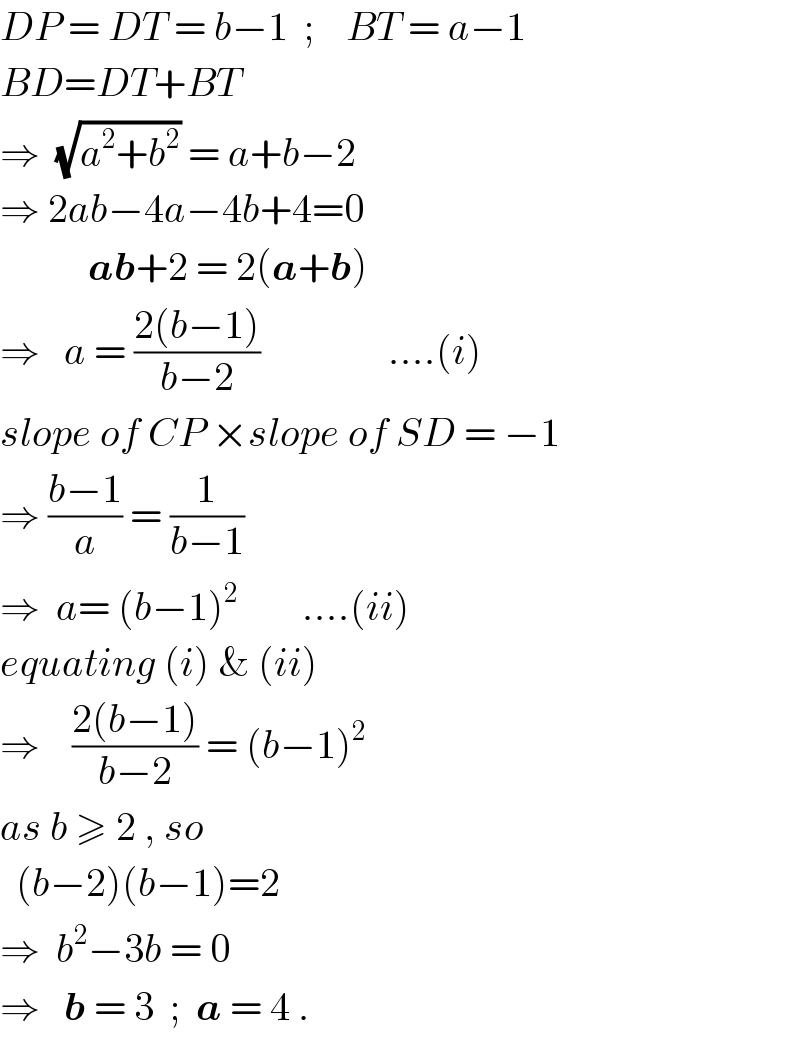
$${DP}\:=\:{DT}\:=\:{b}−\mathrm{1}\:\:;\:\:\:\:{BT}\:=\:{a}−\mathrm{1} \\ $$$${BD}={DT}+{BT} \\ $$$$\Rightarrow\:\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\:=\:{a}+{b}−\mathrm{2}\:\:\: \\ $$$$\Rightarrow\:\mathrm{2}{ab}−\mathrm{4}{a}−\mathrm{4}{b}+\mathrm{4}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{ab}}+\mathrm{2}\:=\:\mathrm{2}\left(\boldsymbol{{a}}+\boldsymbol{{b}}\right)\:\: \\ $$$$\Rightarrow\:\:\:{a}\:=\:\frac{\mathrm{2}\left({b}−\mathrm{1}\right)}{{b}−\mathrm{2}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:….\left({i}\right) \\ $$$${slope}\:{of}\:{CP}\:×{slope}\:{of}\:{SD}\:=\:−\mathrm{1}\: \\ $$$$\Rightarrow\:\frac{{b}−\mathrm{1}}{{a}}\:=\:\frac{\mathrm{1}}{{b}−\mathrm{1}} \\ $$$$\Rightarrow\:\:{a}=\:\left({b}−\mathrm{1}\right)^{\mathrm{2}} \:\:\:\:\:\:\:\:….\left({ii}\right) \\ $$$${equating}\:\left({i}\right)\:\&\:\left({ii}\right) \\ $$$$\Rightarrow\:\:\:\:\frac{\mathrm{2}\left({b}−\mathrm{1}\right)}{{b}−\mathrm{2}}\:=\:\left({b}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$${as}\:{b}\:\geqslant\:\mathrm{2}\:,\:{so} \\ $$$$\:\:\left({b}−\mathrm{2}\right)\left({b}−\mathrm{1}\right)=\mathrm{2} \\ $$$$\Rightarrow\:\:{b}^{\mathrm{2}} −\mathrm{3}{b}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\:\:\boldsymbol{{b}}\:=\:\mathrm{3}\:\:;\:\:\boldsymbol{{a}}\:=\:\mathrm{4}\:. \\ $$
Commented by ajfour last updated on 11/Oct/18

Answered by MrW3 last updated on 11/Oct/18
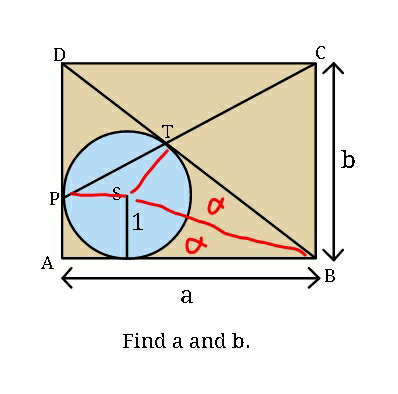
Commented by MrW3 last updated on 11/Oct/18
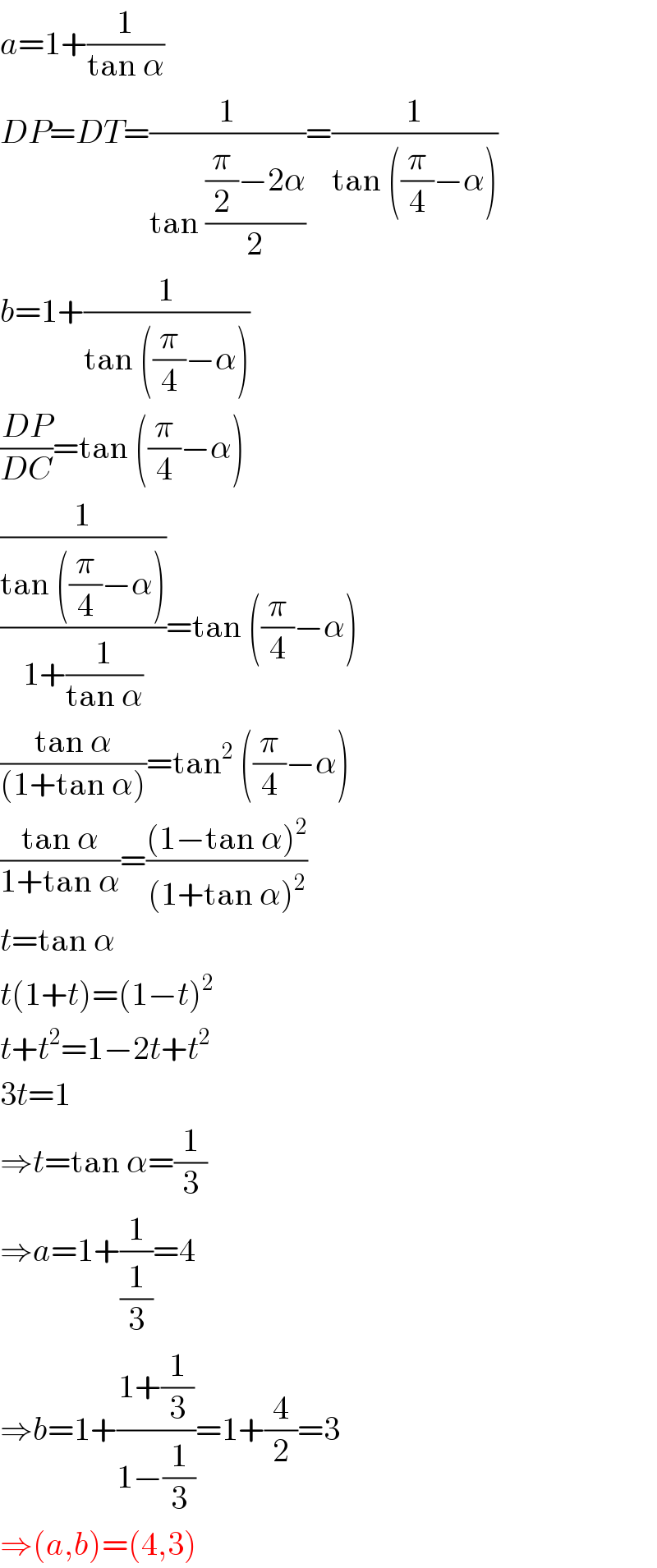
$${a}=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{tan}\:\alpha} \\ $$$${DP}={DT}=\frac{\mathrm{1}}{\mathrm{tan}\:\frac{\frac{\pi}{\mathrm{2}}−\mathrm{2}\alpha}{\mathrm{2}}}=\frac{\mathrm{1}}{\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−\alpha\right)} \\ $$$${b}=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−\alpha\right)} \\ $$$$\frac{{DP}}{{DC}}=\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−\alpha\right) \\ $$$$\frac{\frac{\mathrm{1}}{\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−\alpha\right)}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{tan}\:\alpha}}=\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−\alpha\right) \\ $$$$\frac{\mathrm{tan}\:\alpha}{\left(\mathrm{1}+\mathrm{tan}\:\alpha\right)}=\mathrm{tan}^{\mathrm{2}} \:\left(\frac{\pi}{\mathrm{4}}−\alpha\right) \\ $$$$\frac{\mathrm{tan}\:\alpha}{\mathrm{1}+\mathrm{tan}\:\alpha}=\frac{\left(\mathrm{1}−\mathrm{tan}\:\alpha\right)^{\mathrm{2}} }{\left(\mathrm{1}+\mathrm{tan}\:\alpha\right)^{\mathrm{2}} } \\ $$$${t}=\mathrm{tan}\:\alpha \\ $$$${t}\left(\mathrm{1}+{t}\right)=\left(\mathrm{1}−{t}\right)^{\mathrm{2}} \\ $$$${t}+{t}^{\mathrm{2}} =\mathrm{1}−\mathrm{2}{t}+{t}^{\mathrm{2}} \\ $$$$\mathrm{3}{t}=\mathrm{1} \\ $$$$\Rightarrow{t}=\mathrm{tan}\:\alpha=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow{a}=\mathrm{1}+\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{3}}}=\mathrm{4} \\ $$$$\Rightarrow{b}=\mathrm{1}+\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}}=\mathrm{1}+\frac{\mathrm{4}}{\mathrm{2}}=\mathrm{3} \\ $$$$\Rightarrow\left({a},{b}\right)=\left(\mathrm{4},\mathrm{3}\right) \\ $$
Commented by ajfour last updated on 11/Oct/18

$${thanks}\:{sir}. \\ $$
