Question-45313

Question Number 45313 by ajfour last updated on 11/Oct/18

Commented by ajfour last updated on 11/Oct/18

If all five areas are equal, and circle has unit radius, find a,and b of ellipse.

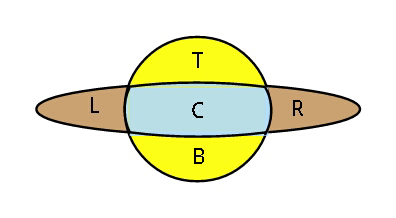
$${If}\:{all}\:{five}\:{areas}\:{are}\:{equal},\:{and} \\ $$$${circle}\:{has}\:{unit}\:{radius},\:{find} \\ $$$$\boldsymbol{{a}},{and}\:\boldsymbol{{b}}\:{of}\:{ellipse}. \\ $$

Answered by MrW3 last updated on 12/Oct/18

area of circle=area of ellipse R=radius of circle=1 area of each region=((πR^2 )/3) eqn. of circle (polar system): r=R eqn. of ellipse (polar system): ((r^2 cos^2 θ)/a^2 )+((r^2 sin^2 θ)/b^2 )=1 ⇒r^2 =((a^2 b^2 )/(a^2 sin^2 θ+b^2 cos^2 θ)) right top intersection point is (r_1 ,θ_1 ) r_1 =R ((a^2 b^2 )/(a^2 sin^2 θ_1 +b^2 cos^2 θ_1 ))=R^2 a^2 sin^2 θ_1 +b^2 cos^2 θ_1 =(((ab)/R))^2 a^2 sin^2 θ_1 +b^2 (1−sin^2 θ_1 )=(((ab)/R))^2 ⇒sin^2 θ_1 =((b^2 (a^2 −R^2 ))/(R^2 (a^2 −b^2 ))) ⇒cos^2 θ_1 =1−((b^2 (a^2 −R^2 ))/(R^2 (a^2 −b^2 )))=((a^2 (R^2 −b^2 ))/(R^2 (a^2 −b^2 ))) ⇒tan θ_1 =(b/a)(√((a^2 −R^2 )/(R^2 −b^2 ))) ⇒θ_1 =tan^(−1) ((b/a)(√((a^2 −R^2 )/(R^2 −b^2 )))) area of rightmost region is A_R =2∫_0 ^θ_1 (1/2)(r^2 −R^2 )dθ =∫_0 ^θ_1 (((a^2 b^2 )/(a^2 sin^2 θ+b^2 cos^2 θ))−R^2 )dθ =a^2 b^2 ∫_0 ^θ_1 (dθ/((a sin θ)^2 +(b cos θ)^2 ))−R^2 θ_1 =ab tan^(−1) (((a tan θ_1 )/b))−R^2 θ_1 =ab tan^(−1) ((√((a^2 −R^2 )/(R^2 −b^2 ))))−R^2 tan^(−1) ((b/a)(√((a^2 −R^2 )/(R^2 −b^2 ))))=((πR^2 )/3) let λ=(a/R)⇒a=λR since πab=πR^2 ⇒ab=R^2 ⇒b=(R^2 /a)=(R/λ) ⇒tan^(−1) λ−tan^(−1) (1/λ)=(π/3) ⇒tan^(−1) λ−((π/2)−tan^(−1) λ)=(π/3) ⇒tan^(−1) λ=((5π)/6) ⇒λ=tan ((5π)/6)=2+(√3) ⇒a=(2+(√3))R ⇒b=(R/(2+(√3)))=(2−(√3))R ⇒θ_1 =tan^(−1) ((1/λ))=tan^(−1) (2−(√3))=15°

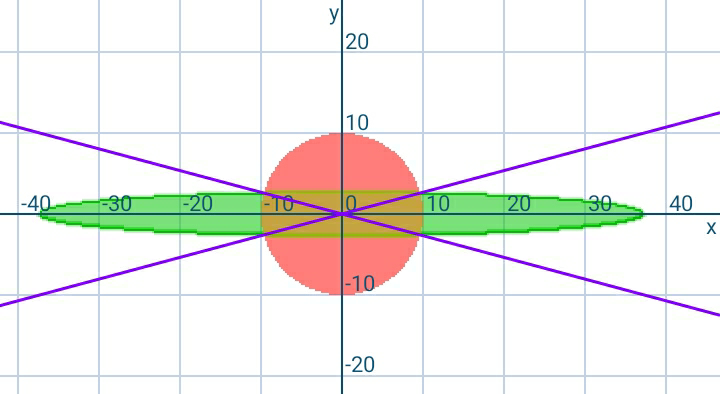
$${area}\:{of}\:{circle}={area}\:{of}\:{ellipse} \\ $$$${R}={radius}\:{of}\:{circle}=\mathrm{1} \\ $$$${area}\:{of}\:{each}\:{region}=\frac{\pi{R}^{\mathrm{2}} }{\mathrm{3}} \\ $$$${eqn}.\:{of}\:{circle}\:\left({polar}\:{system}\right): \\ $$$${r}={R} \\ $$$${eqn}.\:{of}\:{ellipse}\:\left({polar}\:{system}\right): \\ $$$$\frac{{r}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta}{{a}^{\mathrm{2}} }+\frac{{r}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta}{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\Rightarrow{r}^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta+{b}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta} \\ $$$$ \\ $$$${right}\:{top}\:{intersection}\:{point}\:{is}\:\left({r}_{\mathrm{1}} ,\theta_{\mathrm{1}} \right) \\ $$$${r}_{\mathrm{1}} ={R} \\ $$$$\frac{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta_{\mathrm{1}} +{b}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta_{\mathrm{1}} }={R}^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta_{\mathrm{1}} +{b}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta_{\mathrm{1}} =\left(\frac{{ab}}{{R}}\right)^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta_{\mathrm{1}} +{b}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:\theta_{\mathrm{1}} \right)=\left(\frac{{ab}}{{R}}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{sin}^{\mathrm{2}} \:\theta_{\mathrm{1}} =\frac{{b}^{\mathrm{2}} \left({a}^{\mathrm{2}} −{R}^{\mathrm{2}} \right)}{{R}^{\mathrm{2}} \left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)} \\ $$$$\Rightarrow\mathrm{cos}^{\mathrm{2}} \:\theta_{\mathrm{1}} =\mathrm{1}−\frac{{b}^{\mathrm{2}} \left({a}^{\mathrm{2}} −{R}^{\mathrm{2}} \right)}{{R}^{\mathrm{2}} \left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)}=\frac{{a}^{\mathrm{2}} \left({R}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)}{{R}^{\mathrm{2}} \left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)} \\ $$$$\Rightarrow\mathrm{tan}\:\theta_{\mathrm{1}} =\frac{{b}}{{a}}\sqrt{\frac{{a}^{\mathrm{2}} −{R}^{\mathrm{2}} }{{R}^{\mathrm{2}} −{b}^{\mathrm{2}} }} \\ $$$$\Rightarrow\theta_{\mathrm{1}} =\mathrm{tan}^{−\mathrm{1}} \left(\frac{{b}}{{a}}\sqrt{\frac{{a}^{\mathrm{2}} −{R}^{\mathrm{2}} }{{R}^{\mathrm{2}} −{b}^{\mathrm{2}} }}\right) \\ $$$$ \\ $$$${area}\:{of}\:{rightmost}\:{region}\:{is} \\ $$$${A}_{{R}} =\mathrm{2}\int_{\mathrm{0}} ^{\theta_{\mathrm{1}} } \frac{\mathrm{1}}{\mathrm{2}}\left({r}^{\mathrm{2}} −{R}^{\mathrm{2}} \right){d}\theta \\ $$$$=\int_{\mathrm{0}} ^{\theta_{\mathrm{1}} } \left(\frac{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta+{b}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta}−{R}^{\mathrm{2}} \right){d}\theta \\ $$$$={a}^{\mathrm{2}} {b}^{\mathrm{2}} \int_{\mathrm{0}} ^{\theta_{\mathrm{1}} } \frac{{d}\theta}{\left({a}\:\mathrm{sin}\:\theta\right)^{\mathrm{2}} +\left({b}\:\mathrm{cos}\:\theta\right)^{\mathrm{2}} }−{R}^{\mathrm{2}} \theta_{\mathrm{1}} \\ $$$$={ab}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{{a}\:\mathrm{tan}\:\theta_{\mathrm{1}} }{{b}}\right)−{R}^{\mathrm{2}} \theta_{\mathrm{1}} \\ $$$$={ab}\:\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\frac{{a}^{\mathrm{2}} −{R}^{\mathrm{2}} }{{R}^{\mathrm{2}} −{b}^{\mathrm{2}} }}\right)−{R}^{\mathrm{2}} \mathrm{tan}^{−\mathrm{1}} \left(\frac{{b}}{{a}}\sqrt{\frac{{a}^{\mathrm{2}} −{R}^{\mathrm{2}} }{{R}^{\mathrm{2}} −{b}^{\mathrm{2}} }}\right)=\frac{\pi{R}^{\mathrm{2}} }{\mathrm{3}} \\ $$$$ \\ $$$${let}\:\lambda=\frac{{a}}{{R}}\Rightarrow{a}=\lambda{R} \\ $$$${since}\:\pi{ab}=\pi{R}^{\mathrm{2}} \Rightarrow{ab}={R}^{\mathrm{2}} \Rightarrow{b}=\frac{{R}^{\mathrm{2}} }{{a}}=\frac{{R}}{\lambda} \\ $$$$\Rightarrow\mathrm{tan}^{−\mathrm{1}} \lambda−\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\lambda}=\frac{\pi}{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{tan}^{−\mathrm{1}} \lambda−\left(\frac{\pi}{\mathrm{2}}−\mathrm{tan}^{−\mathrm{1}} \lambda\right)=\frac{\pi}{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{tan}^{−\mathrm{1}} \lambda=\frac{\mathrm{5}\pi}{\mathrm{6}} \\ $$$$\Rightarrow\lambda=\mathrm{tan}\:\frac{\mathrm{5}\pi}{\mathrm{6}}=\mathrm{2}+\sqrt{\mathrm{3}} \\ $$$$\Rightarrow{a}=\left(\mathrm{2}+\sqrt{\mathrm{3}}\right){R} \\ $$$$\Rightarrow{b}=\frac{{R}}{\mathrm{2}+\sqrt{\mathrm{3}}}=\left(\mathrm{2}−\sqrt{\mathrm{3}}\right){R} \\ $$$$\Rightarrow\theta_{\mathrm{1}} =\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\lambda}\right)=\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2}−\sqrt{\mathrm{3}}\right)=\mathrm{15}° \\ $$

Commented by MrW3 last updated on 12/Oct/18