Question-45334

Question Number 45334 by Meritguide1234 last updated on 12/Oct/18

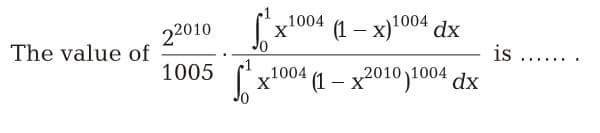
Answered by tanmay.chaudhury50@gmail.com last updated on 12/Oct/18

using gamma beta function ∫_0 ^1 t^(m−1) (1−t)^(n−1) dt=β(m,n)=((⌈(m)⌈(n))/(⌈(m+n))) ⌈(n+1)=n! I_1 =∫_0 ^1 x^(1004) (1−x)^(1004) dx=((⌈(1005)⌈(1005))/(⌈(1005+1005)))←I_1 here m−1=1004 m=1005 n−1=1004 n=1005 I_2 = ∫_0 ^1 x^(1004) (1−x^(2010) )^(1004) dx y=x^(2010) dy=2010 x^(2009) dx x=y^(1/(2010)) dx=(dy/(2010))×(1/((y)^((2009)/(2010)) )) ∫_0 ^1 (y)^((1004)/(2010)) (1−y)^(1004) ×(dy/(2010))×(1/y^((2009)/(2010)) ) =(1/(2010))∫_0 ^1 (y)^((1004−2009)/(2010)) (1−y)^(1004) dy =(1/(2010))∫_0 ^1 y^((−1)/2) (1−y)^(1004) dy =(1/(2010))∫_0 ^1 y^((1/2)−1) (1−y)^(1005−1) dy =(1/(2010))×((⌈((1/2))×⌈(1005))/(⌈(1005+(1/2))))←I_2 ans is (2^(2010) /(1005))×(I_1 /I_2 ) =(2^(2010) /(1005))×((⌈(1005)×⌈(1005))/(⌈(2010)))×2010×((⌈(1005+(1/2)))/(⌈((1/2))×⌈(1005))) =(2^(2010) /(1005))×2010×{⌈(1005)×⌈(1005+(1/2))×2^(2×1005−1) }×(1/2^(2×1005−1) )×(1/(⌈(2010)))×(1/(⌈((1/2)))) =2^(2011) ×{(√π) ×⌈(2010)}×(1/2^(2009) )×(1/( (√π) ×⌈(2010))) =2^(2011−2009) =2^2 =4 so ans is 4 formula 2^(2x−1) ⌈(x)⌈(x+(1/2))=(√π) ×⌈(2x) pls check...

$${using}\:{gamma}\:{beta}\:{function} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{{m}−\mathrm{1}} \left(\mathrm{1}−{t}\right)^{{n}−\mathrm{1}} {dt}=\beta\left({m},{n}\right)=\frac{\lceil\left({m}\right)\lceil\left({n}\right)}{\lceil\left({m}+{n}\right)} \\ $$$$\lceil\left({n}+\mathrm{1}\right)={n}! \\ $$$${I}_{\mathrm{1}} =\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{1004}} \left(\mathrm{1}−{x}\right)^{\mathrm{1004}} {dx}=\frac{\lceil\left(\mathrm{1005}\right)\lceil\left(\mathrm{1005}\right)}{\lceil\left(\mathrm{1005}+\mathrm{1005}\right)}\leftarrow{I}_{\mathrm{1}} \\ $$$$ \\ $$$${here}\:{m}−\mathrm{1}=\mathrm{1004}\:\:\:{m}=\mathrm{1005} \\ $$$$\:\:{n}−\mathrm{1}=\mathrm{1004}\:\:{n}=\mathrm{1005} \\ $$$${I}_{\mathrm{2}} = \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{1004}} \left(\mathrm{1}−{x}^{\mathrm{2010}} \right)^{\mathrm{1004}} {dx} \\ $$$$ \\ $$$${y}={x}^{\mathrm{2010}} \:\:\:{dy}=\mathrm{2010}\:{x}^{\mathrm{2009}} {dx} \\ $$$${x}={y}^{\frac{\mathrm{1}}{\mathrm{2010}}} \\ $$$${dx}=\frac{{dy}}{\mathrm{2010}}×\frac{\mathrm{1}}{\left({y}\right)^{\frac{\mathrm{2009}}{\mathrm{2010}}} } \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \left({y}\right)^{\frac{\mathrm{1004}}{\mathrm{2010}}} \left(\mathrm{1}−{y}\right)^{\mathrm{1004}} ×\frac{{dy}}{\mathrm{2010}}×\frac{\mathrm{1}}{{y}^{\frac{\mathrm{2009}}{\mathrm{2010}}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2010}}\int_{\mathrm{0}} ^{\mathrm{1}} \left({y}\right)^{\frac{\mathrm{1004}−\mathrm{2009}}{\mathrm{2010}}} \left(\mathrm{1}−{y}\right)^{\mathrm{1004}} {dy} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2010}}\int_{\mathrm{0}} ^{\mathrm{1}} {y}^{\frac{−\mathrm{1}}{\mathrm{2}}} \left(\mathrm{1}−{y}\right)^{\mathrm{1004}} {dy} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2010}}\int_{\mathrm{0}} ^{\mathrm{1}} {y}^{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} \left(\mathrm{1}−{y}\right)^{\mathrm{1005}−\mathrm{1}} {dy} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2010}}×\frac{\lceil\left(\frac{\mathrm{1}}{\mathrm{2}}\right)×\lceil\left(\mathrm{1005}\right)}{\lceil\left(\mathrm{1005}+\frac{\mathrm{1}}{\mathrm{2}}\right)}\leftarrow{I}_{\mathrm{2}} \: \\ $$$${ans}\:{is}\:\frac{\mathrm{2}^{\mathrm{2010}} }{\mathrm{1005}}×\frac{{I}_{\mathrm{1}} }{{I}_{\mathrm{2}} } \\ $$$$=\frac{\mathrm{2}^{\mathrm{2010}} }{\mathrm{1005}}×\frac{\lceil\left(\mathrm{1005}\right)×\lceil\left(\mathrm{1005}\right)}{\lceil\left(\mathrm{2010}\right)}×\mathrm{2010}×\frac{\lceil\left(\mathrm{1005}+\frac{\mathrm{1}}{\mathrm{2}}\right)}{\lceil\left(\frac{\mathrm{1}}{\mathrm{2}}\right)×\lceil\left(\mathrm{1005}\right)} \\ $$$$=\frac{\mathrm{2}^{\mathrm{2010}} }{\mathrm{1005}}×\mathrm{2010}×\left\{\lceil\left(\mathrm{1005}\right)×\lceil\left(\mathrm{1005}+\frac{\mathrm{1}}{\mathrm{2}}\right)×\mathrm{2}^{\mathrm{2}×\mathrm{1005}−\mathrm{1}} \right\}×\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}×\mathrm{1005}−\mathrm{1}} }×\frac{\mathrm{1}}{\lceil\left(\mathrm{2010}\right)}×\frac{\mathrm{1}}{\lceil\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} \\ $$$$=\mathrm{2}^{\mathrm{2011}} ×\left\{\sqrt{\pi}\:×\lceil\left(\mathrm{2010}\right)\right\}×\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2009}} }×\frac{\mathrm{1}}{\:\sqrt{\pi}\:×\lceil\left(\mathrm{2010}\right)} \\ $$$$=\mathrm{2}^{\mathrm{2011}−\mathrm{2009}} =\mathrm{2}^{\mathrm{2}} =\mathrm{4}\:\:{so}\:{ans}\:{is}\:\mathrm{4} \\ $$$${formula} \\ $$$$\mathrm{2}^{\mathrm{2}{x}−\mathrm{1}} \lceil\left({x}\right)\lceil\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)=\sqrt{\pi}\:×\lceil\left(\mathrm{2}{x}\right) \\ $$$${pls}\:{check}… \\ $$$$ \\ $$

Commented by Meritguide1234 last updated on 12/Oct/18