Menu Close

Question-45352

Tinku Tara 0 Comments
Pin




Question Number 45352 by Meritguide1234 last updated on 12/Oct/18
Answered by tanmay.chaudhury50@gmail.com last updated on 12/Oct/18
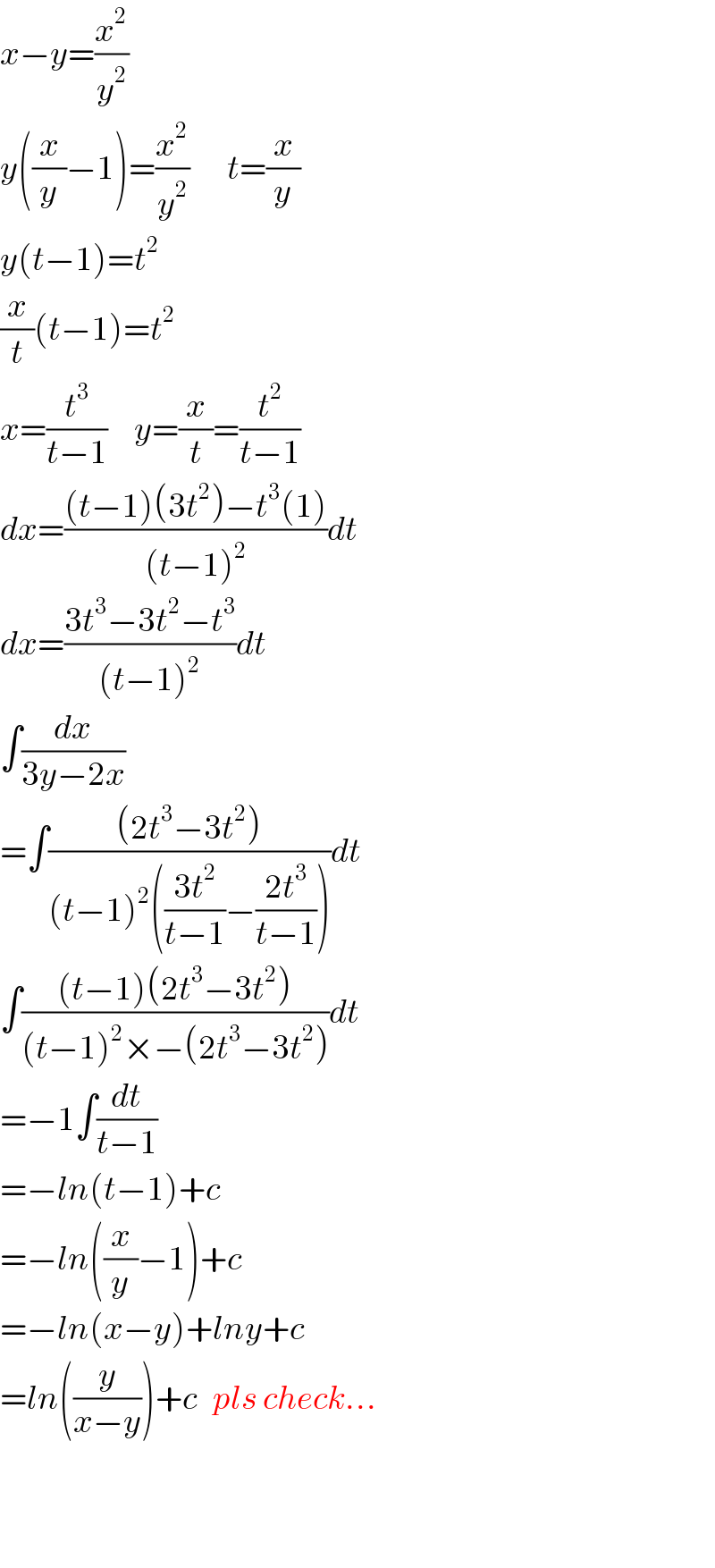
x−y=(x^2 /y^2 ) y((x/y)−1)=(x^2 /y^2 ) t=(x/y) y(t−1)=t^2 (x/t)(t−1)=t^2 x=(t^3 /(t−1)) y=(x/t)=(t^2 /(t−1)) dx=(((t−1)(3t^2 )−t^3 (1))/((t−1)^2 ))dt dx=((3t^3 −3t^2 −t^3 )/((t−1)^2 ))dt ∫(dx/(3y−2x)) =∫(((2t^3 −3t^2 ))/((t−1)^2 (((3t^2 )/(t−1))−((2t^3 )/(t−1)))))dt ∫(((t−1)(2t^3 −3t^2 ))/((t−1)^2 ×−(2t^3 −3t^2 )))dt =−1∫(dt/(t−1)) =−ln(t−1)+c =−ln((x/y)−1)+c =−ln(x−y)+lny+c =ln((y/(x−y)))+c pls check...
$${x}−{y}=\frac{{x}^{\mathrm{2}} }{{y}^{\mathrm{2}} } \\ $$$${y}\left(\frac{{x}}{{y}}−\mathrm{1}\right)=\frac{{x}^{\mathrm{2}} }{{y}^{\mathrm{2}} }\:\:\:\:\:\:\:{t}=\frac{{x}}{{y}} \\ $$$${y}\left({t}−\mathrm{1}\right)={t}^{\mathrm{2}} \\ $$$$\frac{{x}}{{t}}\left({t}−\mathrm{1}\right)={t}^{\mathrm{2}} \\ $$$${x}=\frac{{t}^{\mathrm{3}} }{{t}−\mathrm{1}}\:\:\:\:\:{y}=\frac{{x}}{{t}}=\frac{{t}^{\mathrm{2}} }{{t}−\mathrm{1}} \\ $$$${dx}=\frac{\left({t}−\mathrm{1}\right)\left(\mathrm{3}{t}^{\mathrm{2}} \right)−{t}^{\mathrm{3}} \left(\mathrm{1}\right)}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} }{dt} \\ $$$${dx}=\frac{\mathrm{3}{t}^{\mathrm{3}} −\mathrm{3}{t}^{\mathrm{2}} −{t}^{\mathrm{3}} }{\left({t}−\mathrm{1}\right)^{\mathrm{2}} }{dt} \\ $$$$\int\frac{{dx}}{\mathrm{3}{y}−\mathrm{2}{x}} \\ $$$$=\int\frac{\left(\mathrm{2}{t}^{\mathrm{3}} −\mathrm{3}{t}^{\mathrm{2}} \right)}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} \left(\frac{\mathrm{3}{t}^{\mathrm{2}} }{{t}−\mathrm{1}}−\frac{\mathrm{2}{t}^{\mathrm{3}} }{{t}−\mathrm{1}}\right)}{dt} \\ $$$$\int\frac{\left({t}−\mathrm{1}\right)\left(\mathrm{2}{t}^{\mathrm{3}} −\mathrm{3}{t}^{\mathrm{2}} \right)}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} ×−\left(\mathrm{2}{t}^{\mathrm{3}} −\mathrm{3}{t}^{\mathrm{2}} \right)}{dt} \\ $$$$=−\mathrm{1}\int\frac{{dt}}{{t}−\mathrm{1}} \\ $$$$=−{ln}\left({t}−\mathrm{1}\right)+{c} \\ $$$$=−{ln}\left(\frac{{x}}{{y}}−\mathrm{1}\right)+{c} \\ $$$$=−{ln}\left({x}−{y}\right)+{lny}+{c} \\ $$$$={ln}\left(\frac{{y}}{{x}−{y}}\right)+{c}\:\:\:{pls}\:{check}… \\ $$$$ \\ $$$$ \\ $$
Commented by Meritguide1234 last updated on 12/Oct/18
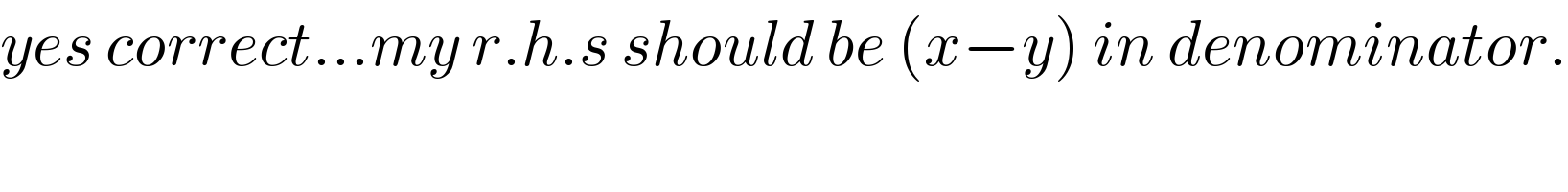
yes correct...my r.h.s should be (x−y) in denominator.
$${yes}\:{correct}…{my}\:{r}.{h}.{s}\:{should}\:{be}\:\left({x}−{y}\right)\:{in}\:{denominator}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *