Question Number 45448 by MrW3 last updated on 13/Oct/18
Commented by MrW3 last updated on 13/Oct/18

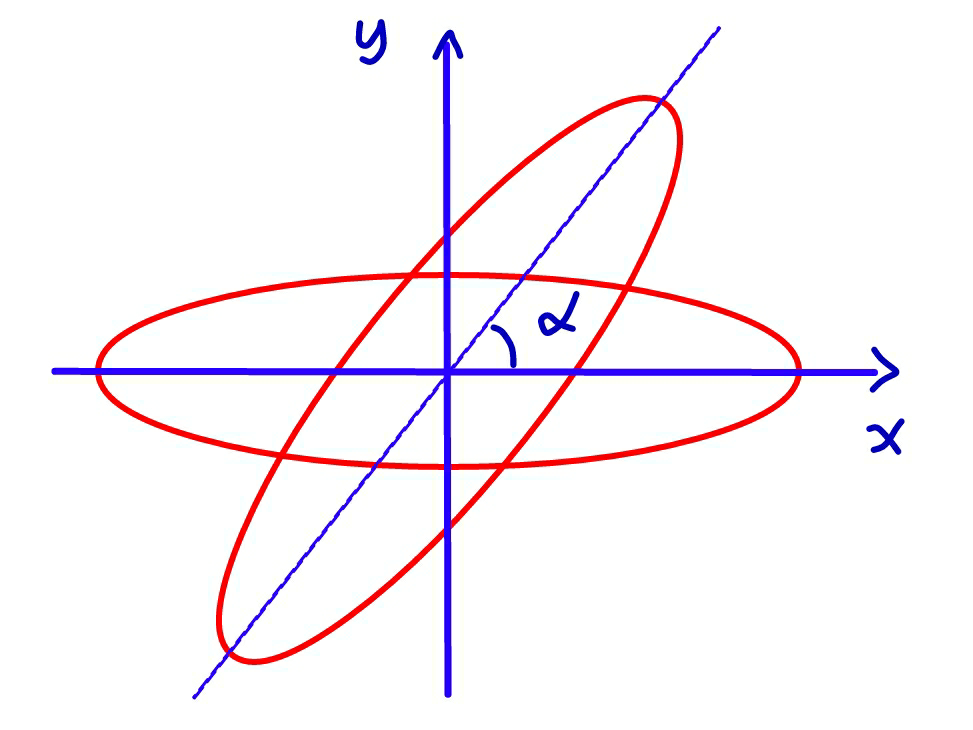
$${When}\:{an}\:{ellipse}\:{is}\:{rotated}\:{by}\:{an} \\ $$$${angle}\:\alpha,\:{the}\:{five}\:{partial}\:{areas}\:{are}\:{equal}. \\ $$$${Find}\:{the}\:{equation}\:{of}\:{the}\:{ellipse} \\ $$$${for}\:\alpha=\mathrm{90}°\:{and}\:\mathrm{45}°\:{respectively}. \\ $$
Commented by ajfour last updated on 13/Oct/18
Commented by ajfour last updated on 13/Oct/18
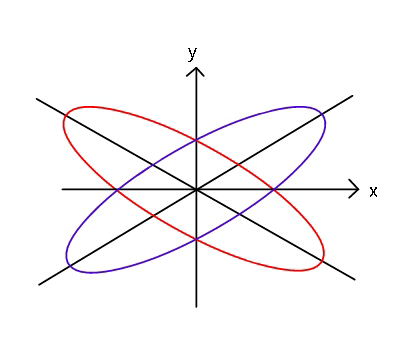
![eq. of blue ellipse: with β=(α/2) ((r^2 cos^2 (θ−β))/a^2 )+((r^2 sin^2 (θ−β))/b^2 )=1 ⇒ r^2 =((a^2 b^2 )/(b^2 cos^2 (θ−β)+a^2 sin^2 (θ−β))) for the red one ((r^2 cos^2 (θ+β))/a^2 )+((r^2 sin^2 (θ+β))/b^2 )=1 Area of blue ellipse in I^(st) quadrant A_b = ((5πab)/(12)) Area of red ellipse in I^(st) quadrant A_r = ((πab)/(12)) A_b =∫_0 ^( π/2) ((r^2 /2)dθ) =((5πab)/(12)) ⇒ ((ab)/2)tan^(−1) [((atan (θ−β))/b)]∣_0 ^(π/2) =((5πab)/(12)) ⇒ tan^(−1) ((a/(btan β)))+tan^(−1) (((atan β)/b))= ((5π)/6) ⇔ φ+ψ = ((5π)/6) , and let m=tan β tan (φ+ψ)= −(1/( (√3))) ⇒ (a/b)((1/m)+m)=−(1/( (√3)))(1−(a^2 /b^2 )) ⇒ ((a/b))^2 − (√3)((1/(sin βcos β)))((a/b))−1=0 ⇒ (a/b) = ((√3)/(sin α))+(√((3/(sin^2 α))+1)) .](https://www.tinkutara.com/question/Q45463.png)
$${eq}.\:{of}\:{blue}\:{ellipse}:\:\:\:{with}\:\beta=\frac{\alpha}{\mathrm{2}} \\ $$$$\:\:\:\:\:\frac{{r}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \left(\theta−\beta\right)}{{a}^{\mathrm{2}} }+\frac{{r}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \left(\theta−\beta\right)}{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\Rightarrow\:{r}^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{{b}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \left(\theta−\beta\right)+{a}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \left(\theta−\beta\right)} \\ $$$$ \\ $$$${for}\:{the}\:{red}\:{one} \\ $$$$\:\:\:\:\:\frac{{r}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \left(\theta+\beta\right)}{{a}^{\mathrm{2}} }+\frac{{r}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \left(\theta+\beta\right)}{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$${Area}\:{of}\:{blue}\:{ellipse}\:{in}\:{I}^{{st}} \:{quadrant} \\ $$$${A}_{{b}} =\:\frac{\mathrm{5}\pi{ab}}{\mathrm{12}} \\ $$$${Area}\:{of}\:{red}\:{ellipse}\:{in}\:{I}^{{st}} {quadrant} \\ $$$$\:\:{A}_{{r}} =\:\frac{\pi{ab}}{\mathrm{12}} \\ $$$$\:{A}_{{b}} =\int_{\mathrm{0}} ^{\:\:\pi/\mathrm{2}} \left(\frac{{r}^{\mathrm{2}} }{\mathrm{2}}{d}\theta\right)\:=\frac{\mathrm{5}\pi{ab}}{\mathrm{12}} \\ $$$$\Rightarrow\:\:\frac{{ab}}{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \left[\frac{{a}\mathrm{tan}\:\left(\theta−\beta\right)}{{b}}\right]\mid_{\mathrm{0}} ^{\pi/\mathrm{2}} =\frac{\mathrm{5}\pi{ab}}{\mathrm{12}} \\ $$$$\Rightarrow\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{{a}}{{b}\mathrm{tan}\:\beta}\right)+\mathrm{tan}^{−\mathrm{1}} \left(\frac{{a}\mathrm{tan}\:\beta}{{b}}\right)=\:\frac{\mathrm{5}\pi}{\mathrm{6}} \\ $$$$\:\:\Leftrightarrow\:\:\phi+\psi\:=\:\frac{\mathrm{5}\pi}{\mathrm{6}}\:\:,\:{and}\:{let}\:{m}=\mathrm{tan}\:\beta \\ $$$$\:\:\:\:\:\:\mathrm{tan}\:\left(\phi+\psi\right)=\:−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow\:\:\:\frac{{a}}{{b}}\left(\frac{\mathrm{1}}{{m}}+{m}\right)=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\left(\mathrm{1}−\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\right) \\ $$$$\Rightarrow\:\left(\frac{{a}}{{b}}\right)^{\mathrm{2}} −\:\sqrt{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{sin}\:\beta\mathrm{cos}\:\beta}\right)\left(\frac{{a}}{{b}}\right)−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\:\frac{{a}}{{b}}\:=\:\frac{\sqrt{\mathrm{3}}}{\mathrm{sin}\:\alpha}+\sqrt{\frac{\mathrm{3}}{\mathrm{sin}\:^{\mathrm{2}} \alpha}+\mathrm{1}}\:\:\:. \\ $$
Commented by ajfour last updated on 13/Oct/18
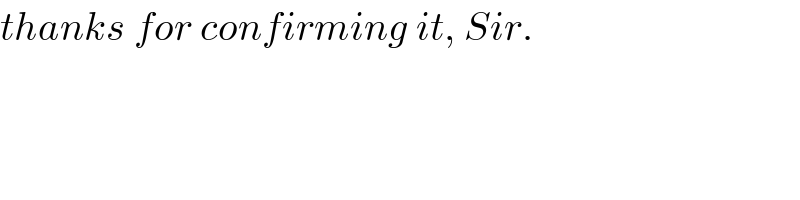
$${thanks}\:{for}\:{confirming}\:{it},\:{Sir}. \\ $$
Commented by MrW3 last updated on 13/Oct/18
$${nice}\:{and}\:{correct}\:{sir}! \\ $$
