Menu Close

Question-45450

Tinku Tara 0 Comments
Pin




Question Number 45450 by Tinkutara last updated on 13/Oct/18
Commented by Meritguide1234 last updated on 14/Oct/18
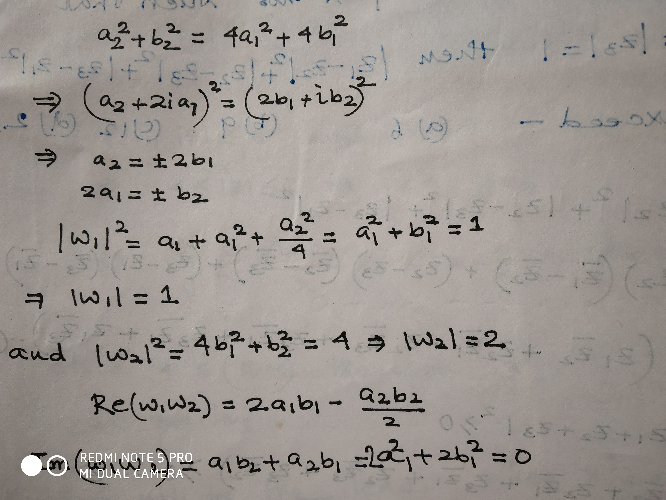
Answered by tanmay.chaudhury50@gmail.com last updated on 13/Oct/18
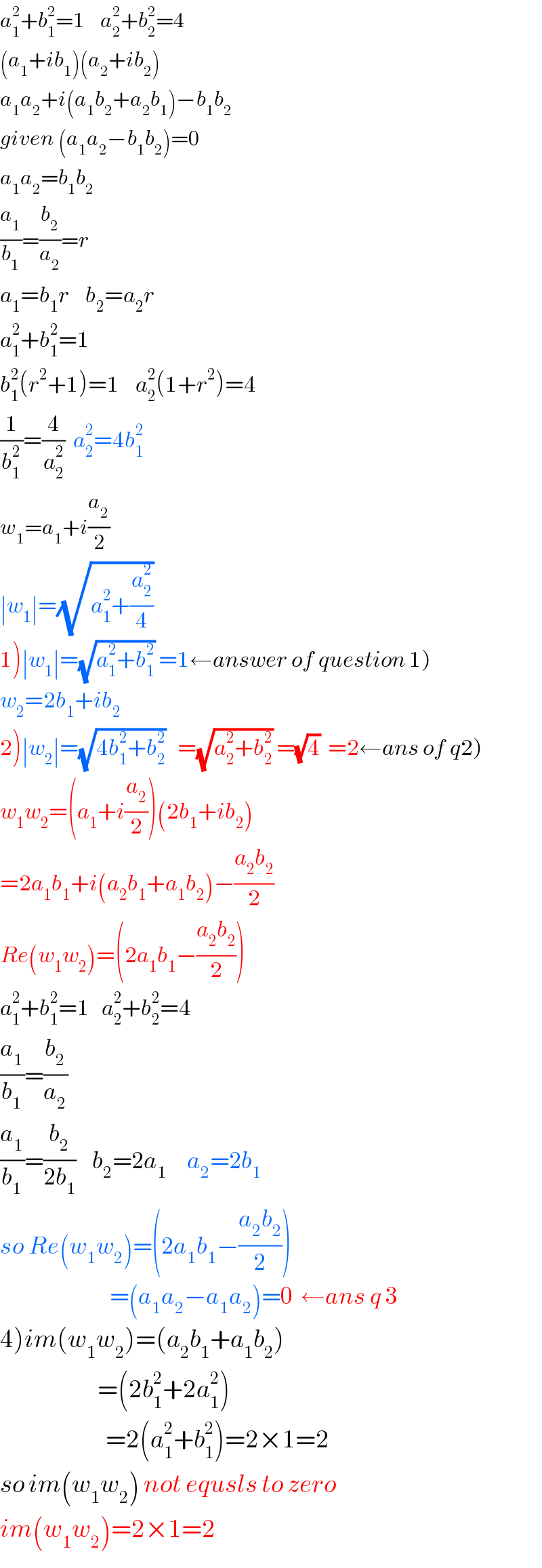
a_1 ^2 +b_1 ^2 =1 a_2 ^2 +b_2 ^2 =4 (a_1 +ib_1 )(a_2 +ib_2 ) a_1 a_2 +i(a_1 b_2 +a_2 b_1 )−b_1 b_2 given (a_1 a_2 −b_1 b_2 )=0 a_1 a_2 =b_1 b_2 (a_1 /b_1 )=(b_2 /a_2 )=r a_1 =b_1 r b_2 =a_2 r a_1 ^2 +b_1 ^2 =1 b_1 ^2 (r^2 +1)=1 a_2 ^2 (1+r^2 )=4 (1/b_1 ^2 )=(4/a_2 ^2 ) a_2 ^2 =4b_1 ^2 w_1 =a_1 +i(a_2 /2) ∣w_1 ∣=(√(a_1 ^2 +(a_2 ^2 /4))) 1)∣w_1 ∣=(√(a_1 ^2 +b_1 ^2 )) =1←answer of question 1) w_2 =2b_1 +ib_2 2)∣w_2 ∣=(√(4b_1 ^2 +b_2 ^2 )) =(√(a_2 ^2 +b_2 ^2 )) =(√4) =2←ans of q2) w_1 w_2 =(a_1 +i(a_2 /2))(2b_1 +ib_2 ) =2a_1 b_1 +i(a_2 b_1 +a_1 b_2 )−((a_2 b_2 )/2) Re(w_1 w_2 )=(2a_1 b_1 −((a_2 b_2 )/2)) a_1 ^2 +b_1 ^2 =1 a_2 ^2 +b_2 ^2 =4 (a_1 /b_1 )=(b_2 /a_2 ) (a_1 /b_1 )=(b_2 /(2b_1 )) b_2 =2a_1 a_2 =2b_1 so Re(w_1 w_2 )=(2a_1 b_1 −((a_2 b_2 )/2)) =(a_1 a_2 −a_1 a_2 )=0 ←ans q 3 4)im(w_1 w_2 )=(a_2 b_1 +a_1 b_2 ) =(2b_1 ^2 +2a_1 ^2 ) =2(a_1 ^2 +b_1 ^2 )=2×1=2 so im(w_1 w_2 ) not equsls to zero im(w_1 w_2 )=2×1=2
$${a}_{\mathrm{1}} ^{\mathrm{2}} +{b}_{\mathrm{1}} ^{\mathrm{2}} =\mathrm{1}\:\:\:\:{a}_{\mathrm{2}} ^{\mathrm{2}} +{b}_{\mathrm{2}} ^{\mathrm{2}} =\mathrm{4} \\ $$$$\left({a}_{\mathrm{1}} +{ib}_{\mathrm{1}} \right)\left({a}_{\mathrm{2}} +{ib}_{\mathrm{2}} \right) \\ $$$${a}_{\mathrm{1}} {a}_{\mathrm{2}} +{i}\left({a}_{\mathrm{1}} {b}_{\mathrm{2}} +{a}_{\mathrm{2}} {b}_{\mathrm{1}} \right)−{b}_{\mathrm{1}} {b}_{\mathrm{2}} \\ $$$${given}\:\left({a}_{\mathrm{1}} {a}_{\mathrm{2}} −{b}_{\mathrm{1}} {b}_{\mathrm{2}} \right)=\mathrm{0} \\ $$$${a}_{\mathrm{1}} {a}_{\mathrm{2}} ={b}_{\mathrm{1}} {b}_{\mathrm{2}} \\ $$$$\frac{{a}_{\mathrm{1}} }{{b}_{\mathrm{1}} }=\frac{{b}_{\mathrm{2}} }{{a}_{\mathrm{2}} }={r} \\ $$$${a}_{\mathrm{1}} ={b}_{\mathrm{1}} {r}\:\:\:\:{b}_{\mathrm{2}} ={a}_{\mathrm{2}} {r} \\ $$$${a}_{\mathrm{1}} ^{\mathrm{2}} +{b}_{\mathrm{1}} ^{\mathrm{2}} =\mathrm{1} \\ $$$${b}_{\mathrm{1}} ^{\mathrm{2}} \left({r}^{\mathrm{2}} +\mathrm{1}\right)=\mathrm{1}\:\:\:\:{a}_{\mathrm{2}} ^{\mathrm{2}} \left(\mathrm{1}+{r}^{\mathrm{2}} \right)=\mathrm{4} \\ $$$$\frac{\mathrm{1}}{{b}_{\mathrm{1}} ^{\mathrm{2}} }=\frac{\mathrm{4}}{{a}_{\mathrm{2}} ^{\mathrm{2}} }\:\:{a}_{\mathrm{2}} ^{\mathrm{2}} =\mathrm{4}{b}_{\mathrm{1}} ^{\mathrm{2}} \:\:\:\: \\ $$$${w}_{\mathrm{1}} ={a}_{\mathrm{1}} +{i}\frac{{a}_{\mathrm{2}} }{\mathrm{2}} \\ $$$$\mid{w}_{\mathrm{1}} \mid=\sqrt{{a}_{\mathrm{1}} ^{\mathrm{2}} +\frac{{a}_{\mathrm{2}} ^{\mathrm{2}} }{\mathrm{4}}}\: \\ $$$$\left.\mathrm{1}\left.\right)\mid{w}_{\mathrm{1}} \mid=\sqrt{{a}_{\mathrm{1}} ^{\mathrm{2}} +{b}_{\mathrm{1}} ^{\mathrm{2}} }\:=\mathrm{1}\leftarrow{answer}\:{of}\:{question}\:\mathrm{1}\right) \\ $$$${w}_{\mathrm{2}} =\mathrm{2}{b}_{\mathrm{1}} +{ib}_{\mathrm{2}} \\ $$$$\left.\mathrm{2}\left.\right)\mid{w}_{\mathrm{2}} \mid=\sqrt{\mathrm{4}{b}_{\mathrm{1}} ^{\mathrm{2}} +{b}_{\mathrm{2}} ^{\mathrm{2}} }\:\:\:=\sqrt{{a}_{\mathrm{2}} ^{\mathrm{2}} +{b}_{\mathrm{2}} ^{\mathrm{2}} }\:=\sqrt{\mathrm{4}}\:\:=\mathrm{2}\leftarrow{ans}\:{of}\:{q}\mathrm{2}\right) \\ $$$${w}_{\mathrm{1}} {w}_{\mathrm{2}} =\left({a}_{\mathrm{1}} +{i}\frac{{a}_{\mathrm{2}} }{\mathrm{2}}\right)\left(\mathrm{2}{b}_{\mathrm{1}} +{ib}_{\mathrm{2}} \right) \\ $$$$=\mathrm{2}{a}_{\mathrm{1}} {b}_{\mathrm{1}} +{i}\left({a}_{\mathrm{2}} {b}_{\mathrm{1}} +{a}_{\mathrm{1}} {b}_{\mathrm{2}} \right)−\frac{{a}_{\mathrm{2}} {b}_{\mathrm{2}} }{\mathrm{2}} \\ $$$${Re}\left({w}_{\mathrm{1}} {w}_{\mathrm{2}} \right)=\left(\mathrm{2}{a}_{\mathrm{1}} {b}_{\mathrm{1}} −\frac{{a}_{\mathrm{2}} {b}_{\mathrm{2}} }{\mathrm{2}}\right) \\ $$$${a}_{\mathrm{1}} ^{\mathrm{2}} +{b}_{\mathrm{1}} ^{\mathrm{2}} =\mathrm{1}\:\:\:{a}_{\mathrm{2}} ^{\mathrm{2}} +{b}_{\mathrm{2}} ^{\mathrm{2}} =\mathrm{4} \\ $$$$\frac{{a}_{\mathrm{1}} }{{b}_{\mathrm{1}} }=\frac{{b}_{\mathrm{2}} }{{a}_{\mathrm{2}} } \\ $$$$\frac{{a}_{\mathrm{1}} }{{b}_{\mathrm{1}} }=\frac{{b}_{\mathrm{2}} }{\mathrm{2}{b}_{\mathrm{1}} }\:\:\:\:{b}_{\mathrm{2}} =\mathrm{2}{a}_{\mathrm{1}} \:\:\:\:\:{a}_{\mathrm{2}} =\mathrm{2}{b}_{\mathrm{1}} \\ $$$${so}\:{Re}\left({w}_{\mathrm{1}} {w}_{\mathrm{2}} \right)=\left(\mathrm{2}{a}_{\mathrm{1}} {b}_{\mathrm{1}} −\frac{{a}_{\mathrm{2}} {b}_{\mathrm{2}} }{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left({a}_{\mathrm{1}} {a}_{\mathrm{2}} −{a}_{\mathrm{1}} {a}_{\mathrm{2}} \right)=\mathrm{0}\:\:\leftarrow{ans}\:{q}\:\mathrm{3} \\ $$$$\left.\mathrm{4}\right){im}\left({w}_{\mathrm{1}} {w}_{\mathrm{2}} \right)=\left({a}_{\mathrm{2}} {b}_{\mathrm{1}} +{a}_{\mathrm{1}} {b}_{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(\mathrm{2}{b}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{2}{a}_{\mathrm{1}} ^{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}\left({a}_{\mathrm{1}} ^{\mathrm{2}} +{b}_{\mathrm{1}} ^{\mathrm{2}} \right)=\mathrm{2}×\mathrm{1}=\mathrm{2} \\ $$$${so}\:{im}\left({w}_{\mathrm{1}} {w}_{\mathrm{2}} \right)\:{not}\:{equsls}\:{to}\:{zero} \\ $$$${im}\left({w}_{\mathrm{1}} {w}_{\mathrm{2}} \right)=\mathrm{2}×\mathrm{1}=\mathrm{2} \\ $$
Commented by Tinkutara last updated on 13/Oct/18
Thank you very much Sir! I got the answer. ��������
Commented by tanmay.chaudhury50@gmail.com last updated on 13/Oct/18
thank you also for creating such platform to engage our mind..
$${thank}\:{you}\:{also}\:{for}\:{creating}\:{such}\:{platform} \\ $$$${to}\:{engage}\:{our}\:{mind}.. \\ $$
Commented by Tinkutara last updated on 13/Oct/18
Sorry Sir, but I am not the developer of this app. I am just a user like you.

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *