Question-45456

Question Number 45456 by peter frank last updated on 13/Oct/18

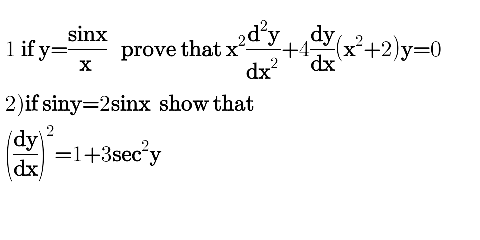
Commented by peter frank last updated on 13/Oct/18

$$\mathrm{math1967} \\ $$

Commented by math1967 last updated on 13/Oct/18

y=((sinx)/x) xy=sinx⇒y+x(dy/dx)=cosx (dy/dx) +(dy/dx) +x(d^2 y/dx^2 )=−sinx x(d^2 y/dx^2 ) +2(dy/dx)=−xy [xy=sinx] x^2 (d^2 y/dx^2 ) +2x(dy/dx) +x^2 y=0 can not match....

$${y}=\frac{{sinx}}{{x}} \\ $$$${xy}={sinx}\Rightarrow{y}+{x}\frac{{dy}}{{dx}}={cosx} \\ $$$$\frac{{dy}}{{dx}}\:+\frac{{dy}}{{dx}}\:+{x}\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=−{sinx} \\ $$$${x}\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:+\mathrm{2}\frac{{dy}}{{dx}}=−{xy}\:\:\:\left[{xy}={sinx}\right] \\ $$$${x}^{\mathrm{2}} \frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:+\mathrm{2}{x}\frac{{dy}}{{dx}}\:+{x}^{\mathrm{2}} {y}=\mathrm{0} \\ $$$${can}\:{not}\:{match}…. \\ $$

Commented by maxmathsup by imad last updated on 14/Oct/18

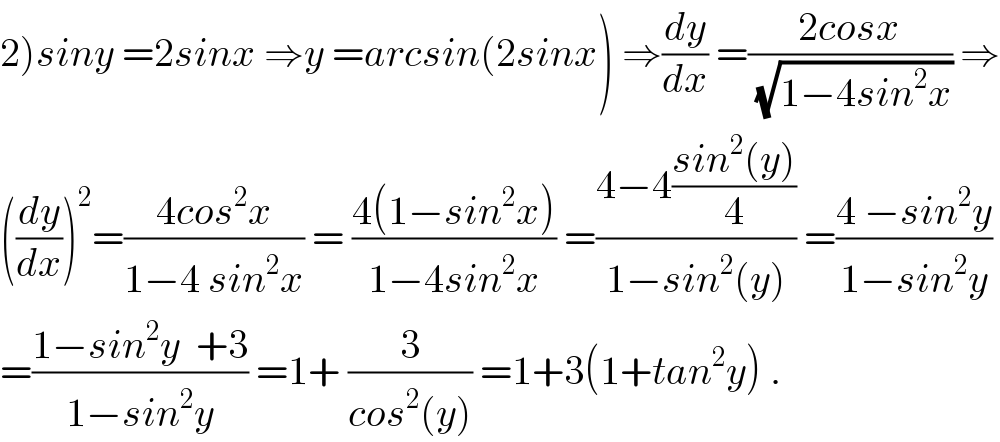
2)siny =2sinx ⇒y =arcsin(2sinx) ⇒(dy/dx) =((2cosx)/( (√(1−4sin^2 x)))) ⇒ ((dy/dx))^2 =((4cos^2 x)/(1−4 sin^2 x)) = ((4(1−sin^2 x))/(1−4sin^2 x)) =((4−4((sin^2 (y))/4))/(1−sin^2 (y))) =((4 −sin^2 y)/(1−sin^2 y)) =((1−sin^2 y +3)/(1−sin^2 y)) =1+ (3/(cos^2 (y))) =1+3(1+tan^2 y) .

$$\left.\mathrm{2}\right){siny}\:=\mathrm{2}{sinx}\:\Rightarrow{y}\:={arcsin}\left(\mathrm{2}{sinx}\right)\:\Rightarrow\frac{{dy}}{{dx}}\:=\frac{\mathrm{2}{cosx}}{\:\sqrt{\mathrm{1}−\mathrm{4}{sin}^{\mathrm{2}} {x}}}\:\Rightarrow \\ $$$$\left(\frac{{dy}}{{dx}}\right)^{\mathrm{2}} =\frac{\mathrm{4}{cos}^{\mathrm{2}} {x}}{\mathrm{1}−\mathrm{4}\:{sin}^{\mathrm{2}} {x}}\:=\:\frac{\mathrm{4}\left(\mathrm{1}−{sin}^{\mathrm{2}} {x}\right)}{\mathrm{1}−\mathrm{4}{sin}^{\mathrm{2}} {x}}\:=\frac{\mathrm{4}−\mathrm{4}\frac{{sin}^{\mathrm{2}} \left({y}\right)}{\mathrm{4}}}{\mathrm{1}−{sin}^{\mathrm{2}} \left({y}\right)}\:=\frac{\mathrm{4}\:−{sin}^{\mathrm{2}} {y}}{\mathrm{1}−{sin}^{\mathrm{2}} {y}} \\ $$$$=\frac{\mathrm{1}−{sin}^{\mathrm{2}} {y}\:\:+\mathrm{3}}{\mathrm{1}−{sin}^{\mathrm{2}} {y}}\:=\mathrm{1}+\:\frac{\mathrm{3}}{{cos}^{\mathrm{2}} \left({y}\right)}\:=\mathrm{1}+\mathrm{3}\left(\mathrm{1}+{tan}^{\mathrm{2}} {y}\right)\:. \\ $$

Commented by peter frank last updated on 14/Oct/18

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}.\mathrm{i}\:\mathrm{also}\:\mathrm{had}\:\mathrm{such}\:\mathrm{doubt} \\ $$

Commented by peter frank last updated on 14/Oct/18

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 13/Oct/18

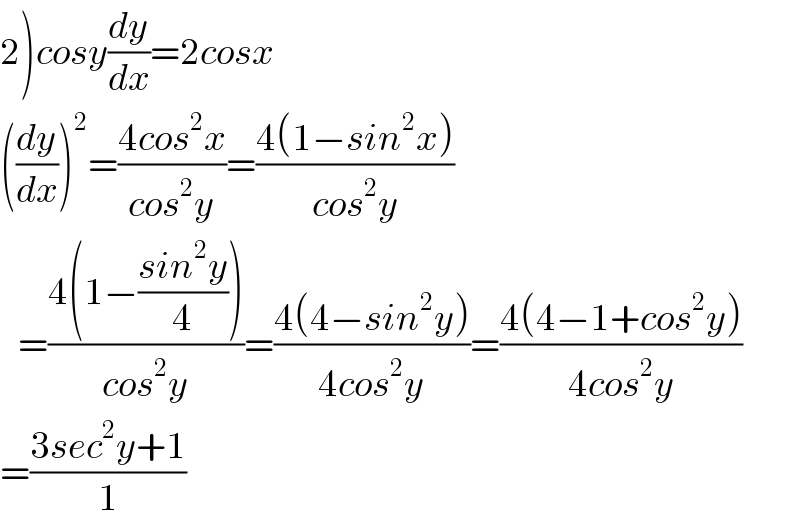
2)cosy(dy/dx)=2cosx ((dy/dx))^2 =((4cos^2 x)/(cos^2 y))=((4(1−sin^2 x))/(cos^2 y)) =((4(1−((sin^2 y)/4)))/(cos^2 y))=((4(4−sin^2 y))/(4cos^2 y))=((4(4−1+cos^2 y))/(4cos^2 y)) =((3sec^2 y+1)/1)

$$\left.\mathrm{2}\right){cosy}\frac{{dy}}{{dx}}=\mathrm{2}{cosx} \\ $$$$\left(\frac{{dy}}{{dx}}\right)^{\mathrm{2}} =\frac{\mathrm{4}{cos}^{\mathrm{2}} {x}}{{cos}^{\mathrm{2}} {y}}=\frac{\mathrm{4}\left(\mathrm{1}−{sin}^{\mathrm{2}} {x}\right)}{{cos}^{\mathrm{2}} {y}} \\ $$$$\:\:\:=\frac{\mathrm{4}\left(\mathrm{1}−\frac{{sin}^{\mathrm{2}} {y}}{\mathrm{4}}\right)}{{cos}^{\mathrm{2}} {y}}=\frac{\mathrm{4}\left(\mathrm{4}−{sin}^{\mathrm{2}} {y}\right)}{\mathrm{4}{cos}^{\mathrm{2}} {y}}=\frac{\mathrm{4}\left(\mathrm{4}−\mathrm{1}+{cos}^{\mathrm{2}} {y}\right)}{\mathrm{4}{cos}^{\mathrm{2}} {y}} \\ $$$$=\frac{\mathrm{3}{sec}^{\mathrm{2}} {y}+\mathrm{1}}{\mathrm{1}} \\ $$

Commented by peter frank last updated on 14/Oct/18

$$\mathrm{thank}\:\mathrm{you} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply