Question Number 45482 by Meritguide1234 last updated on 13/Oct/18
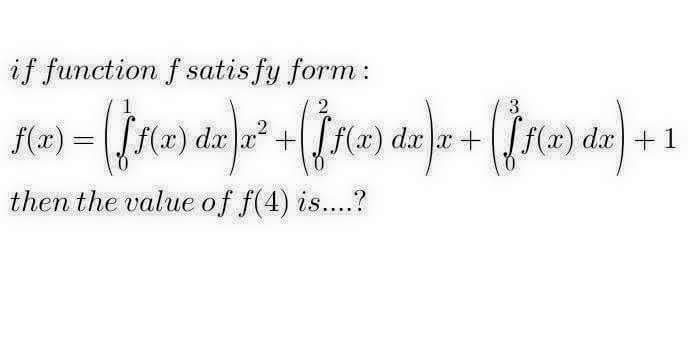
Answered by ajfour last updated on 13/Oct/18
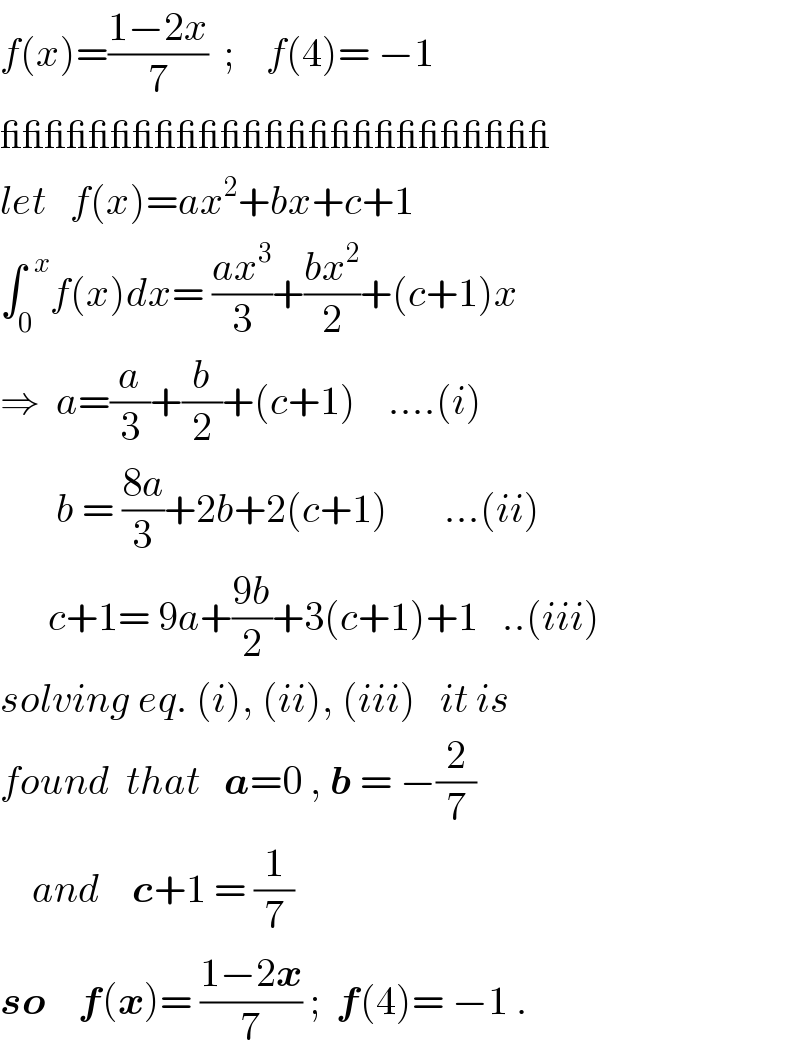
$${f}\left({x}\right)=\frac{\mathrm{1}−\mathrm{2}{x}}{\mathrm{7}}\:\:;\:\:\:\:{f}\left(\mathrm{4}\right)=\:−\mathrm{1}\: \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$${let}\:\:\:{f}\left({x}\right)={ax}^{\mathrm{2}} +{bx}+{c}+\mathrm{1} \\ $$$$\int_{\mathrm{0}} ^{\:\:{x}} {f}\left({x}\right){dx}=\:\frac{{ax}^{\mathrm{3}} }{\mathrm{3}}+\frac{{bx}^{\mathrm{2}} }{\mathrm{2}}+\left({c}+\mathrm{1}\right){x} \\ $$$$\Rightarrow\:\:{a}=\frac{{a}}{\mathrm{3}}+\frac{{b}}{\mathrm{2}}+\left({c}+\mathrm{1}\right)\:\:\:\:….\left({i}\right) \\ $$$$\:\:\:\:\:\:\:{b}\:=\:\frac{\mathrm{8}{a}}{\mathrm{3}}+\mathrm{2}{b}+\mathrm{2}\left({c}+\mathrm{1}\right)\:\:\:\:\:\:\:…\left({ii}\right) \\ $$$$\:\:\:\:\:\:{c}+\mathrm{1}=\:\mathrm{9}{a}+\frac{\mathrm{9}{b}}{\mathrm{2}}+\mathrm{3}\left({c}+\mathrm{1}\right)+\mathrm{1}\:\:\:..\left({iii}\right) \\ $$$${solving}\:{eq}.\:\left({i}\right),\:\left({ii}\right),\:\left({iii}\right)\:\:\:{it}\:{is} \\ $$$${found}\:\:{that}\:\:\:\boldsymbol{{a}}=\mathrm{0}\:,\:\boldsymbol{{b}}\:=\:−\frac{\mathrm{2}}{\mathrm{7}} \\ $$$$\:\:\:\:{and}\:\:\:\:\boldsymbol{{c}}+\mathrm{1}\:=\:\frac{\mathrm{1}}{\mathrm{7}}\: \\ $$$$\boldsymbol{{so}}\:\:\:\:\boldsymbol{{f}}\left(\boldsymbol{{x}}\right)=\:\frac{\mathrm{1}−\mathrm{2}\boldsymbol{{x}}}{\mathrm{7}}\:;\:\:\boldsymbol{{f}}\left(\mathrm{4}\right)=\:−\mathrm{1}\:. \\ $$
Commented by Meritguide1234 last updated on 13/Oct/18
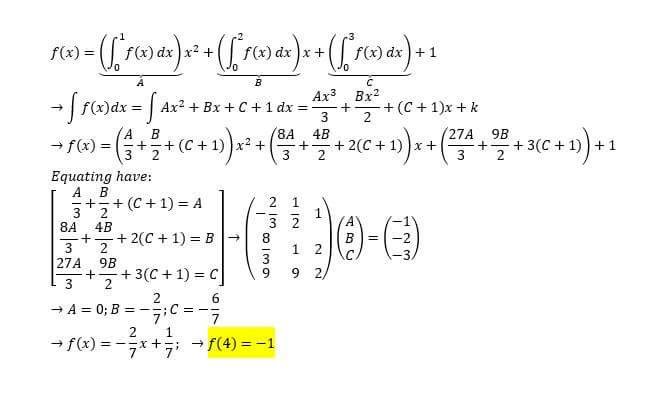
Commented by Meritguide1234 last updated on 13/Oct/18
$${very}\:{nice}\:{solution} \\ $$
Commented by rahul 19 last updated on 13/Oct/18
perfect solution.
@Meritguide keep posting a problem a day in Calculus .( definite integration)
I like your problems.
