Question-45495

Question Number 45495 by Meritguide1234 last updated on 13/Oct/18

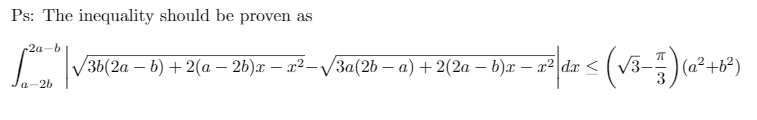
Answered by tanmay.chaudhury50@gmail.com last updated on 13/Oct/18

Commented by tanmay.chaudhury50@gmail.com last updated on 14/Oct/18

\int_{a - 2 b}^{2 a - b} ∣ \sqrt{(x + 3 b) ((2 a - b - x)} - \sqrt{(3 a - x) (2 b - a + x)} ∣ d x

\int_{a - 2 b}^{2 a - b} \sqrt{(3 a - 3 b - x + 3 b) \times (2 a - b - (3 a - 3 b - x)} - \sqrt{(3 a - x) (2 b - a + x)} ∣ d x

\int_{a - 2 b}^{2 a - b} ∣ \sqrt{(3 a - x) (2 b - a - x)} - \sqrt{(x + 3 b) (2 a - b - x)} d x

\int_{a - 2 b}^{2 a - b} ∣ p - q ∣ d x = \int_{a - 2 b}^{2 a - b} ∣ q - p ∣ d x

t h a t m e a n s p - q = q - p

2 p = 2 q p = q

(x + 3 b) (2 a - b - x) = (3 a - x) (2 b - a - x)

2 a x - b x - x^{2} + 6 a b - 3 b^{2} - 3 b x = 6 a b - 3 a^{2} - 3 a x - 2 b x + a x + x^{2}

2 a x + 2 a x - 4 b x + 2 b x - x^{2} - x^{2} + 6 a b - 6 a b = 0

4 a x - 2 b x - 2 x^{2} = 0

2 x (2 a - b - x) = 0

x = 2 a - b