Question Number 45527 by Sanjarbek last updated on 14/Oct/18
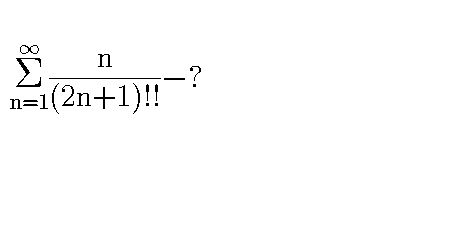
Commented by Meritguide1234 last updated on 14/Oct/18

Commented by maxmathsup by imad last updated on 14/Oct/18
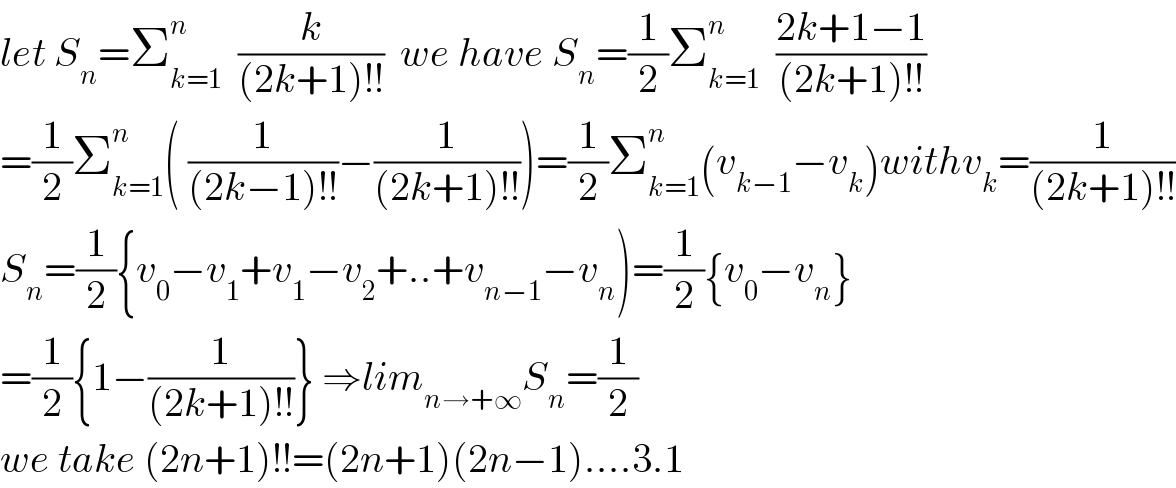
$${let}\:{S}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\frac{{k}}{\left(\mathrm{2}{k}+\mathrm{1}\right)!!}\:\:{we}\:{have}\:{S}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\frac{\mathrm{2}{k}+\mathrm{1}−\mathrm{1}}{\left(\mathrm{2}{k}+\mathrm{1}\right)!!} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\sum_{{k}=\mathrm{1}} ^{{n}} \left(\:\frac{\mathrm{1}}{\left(\mathrm{2}{k}−\mathrm{1}\right)!!}−\frac{\mathrm{1}}{\left(\mathrm{2}{k}+\mathrm{1}\right)!!}\right)=\frac{\mathrm{1}}{\mathrm{2}}\sum_{{k}=\mathrm{1}} ^{{n}} \left({v}_{{k}−\mathrm{1}} −{v}_{{k}} \right){withv}_{{k}} =\frac{\mathrm{1}}{\left(\mathrm{2}{k}+\mathrm{1}\right)!!} \\ $$$${S}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}\left\{{v}_{\mathrm{0}} −{v}_{\mathrm{1}} +{v}_{\mathrm{1}} −{v}_{\mathrm{2}} +..+{v}_{{n}−\mathrm{1}} −{v}_{{n}} \right)=\frac{\mathrm{1}}{\mathrm{2}}\left\{{v}_{\mathrm{0}} −{v}_{{n}} \right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{\mathrm{1}−\frac{\mathrm{1}}{\left(\mathrm{2}{k}+\mathrm{1}\right)!!}\right\}\:\Rightarrow{lim}_{{n}\rightarrow+\infty} {S}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${we}\:{take}\:\left(\mathrm{2}{n}+\mathrm{1}\right)!!=\left(\mathrm{2}{n}+\mathrm{1}\right)\left(\mathrm{2}{n}−\mathrm{1}\right)….\mathrm{3}.\mathrm{1} \\ $$
