Question Number 45539 by rahul 19 last updated on 14/Oct/18

Commented by rahul 19 last updated on 14/Oct/18
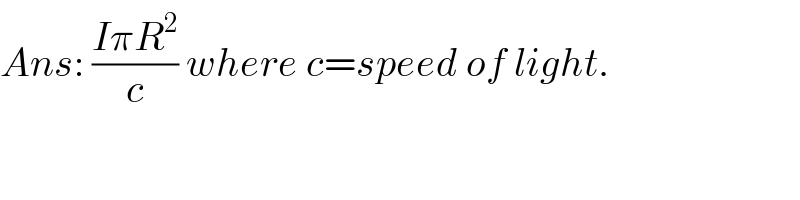
$${Ans}:\:\frac{{I}\pi{R}^{\mathrm{2}} }{{c}}\:{where}\:{c}={speed}\:{of}\:{light}. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 14/Oct/18

Answered by tanmay.chaudhury50@gmail.com last updated on 14/Oct/18

$${intensity}={I}\:\left({w}/{m}^{\mathrm{2}} \right) \\ $$$${projected}\:{eross}\:{sectional}\:{area}\:{of}\:{light}\:{beam}\:{that}\:{strike}\:{sphere}\:{is} \\ $$$$\pi{R}^{\mathrm{2}} \: \\ $$$$\left({power}={force}×{velocity}\right. \\ $$$${force}=\frac{{power}}{{velocity}}=\frac{{I}}{{c}}\:{per}\:{unit}\:{area} \\ $$$${so}\:{force}\:{exerted}\:{by}\:{photons}\:{coming}\:{throuvh} \\ $$$${projected}\:{cross}\:{sectional}\:{area}\:\pi{R}^{\mathrm{2}} \:{is} \\ $$$${F}_{{B}} =\frac{{I}}{{c}}×\pi{R}^{\mathrm{2}} \:\:\left({for}\:{perfectly}\:{black}\:{body}\right) \\ $$$${F}_{{R}} =\frac{{I}}{{c}}×\pi{R}^{\mathrm{2}} ×\mathrm{2}\:\:\left({for}\:{reflecting}\:{surface}\right) \\ $$$${for}\:{better}\:{understsnding}\:{visit}\:{youtube}\:{video}… \\ $$$$ \\ $$
Commented by rahul 19 last updated on 14/Oct/18
Thank you so much sir ! ☺️������
