Menu Close

Question-45575

Tinku Tara 0 Comments
Pin




Question Number 45575 by rahul 19 last updated on 14/Oct/18
Commented by rahul 19 last updated on 14/Oct/18
My doubt: If i will take both points on same side of plane (wrong method) and will take points on opposite side i will get same answer.... it is always true? right???
$${My}\:{doubt}: \\ $$$${If}\:{i}\:{will}\:{take}\:{both}\:{points}\:{on}\:{same}\:{side} \\ $$$${of}\:{plane}\:\left({wrong}\:{method}\right)\:{and}\:{will} \\ $$$${take}\:{points}\:{on}\:{opposite}\:{side}\:{i}\:{will}\:{get}\: \\ $$$${same}\:{answer}….\:\:{it}\:{is}\:{always}\:{true}? \\ $$$${right}??? \\ $$
Commented by MrW3 last updated on 14/Oct/18
Commented by MrW3 last updated on 14/Oct/18
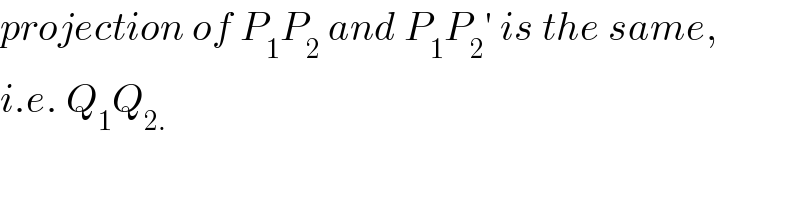
projection of P_1 P_2 and P_1 P_2 ′ is the same, i.e. Q_1 Q_(2.)
$${projection}\:{of}\:{P}_{\mathrm{1}} {P}_{\mathrm{2}} \:{and}\:{P}_{\mathrm{1}} {P}_{\mathrm{2}} '\:{is}\:{the}\:{same}, \\ $$$${i}.{e}.\:{Q}_{\mathrm{1}} {Q}_{\mathrm{2}.} \\ $$
Commented by rahul 19 last updated on 14/Oct/18
thanks sir!
$${thanks}\:{sir}! \\ $$
Answered by MrW3 last updated on 14/Oct/18
projection of point (5,−1,4) is (x_1 ,y_1 ,z_1 ): x_1 =5−((1×(5−1+4−7))/3)=5−((1×1)/3)=((14)/3) y_1 =−1−((1×(5−1+4−7))/3)=−1−((1×1)/3)=−(4/3) z_1 =4−((1×(5−1+4−7))/3)=4−((1×1)/3)=((11)/3) projection of point (4,−1,3) is (x_2 ,y_2 ,z_2 ): x_2 =4−((1×(4−1+3−7))/3)=4−((1×(−1))/3)=((13)/3) y_2 =−1−((1×(4−1+3−7))/3)=−1−((1×(−1))/3)=−(2/3) z_2 =3−((1×(4−1+3−7))/3)=3−((1×(−1))/3)=((10)/3) length of projection: L=(1/3)(√((14−13)^2 +(−4+2)^2 +(11−10)^2 ))=(√(2/3))
$${projection}\:{of}\:{point}\:\left(\mathrm{5},−\mathrm{1},\mathrm{4}\right)\:{is}\:\left({x}_{\mathrm{1}} ,{y}_{\mathrm{1}} ,{z}_{\mathrm{1}} \right): \\ $$$${x}_{\mathrm{1}} =\mathrm{5}−\frac{\mathrm{1}×\left(\mathrm{5}−\mathrm{1}+\mathrm{4}−\mathrm{7}\right)}{\mathrm{3}}=\mathrm{5}−\frac{\mathrm{1}×\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{14}}{\mathrm{3}} \\ $$$${y}_{\mathrm{1}} =−\mathrm{1}−\frac{\mathrm{1}×\left(\mathrm{5}−\mathrm{1}+\mathrm{4}−\mathrm{7}\right)}{\mathrm{3}}=−\mathrm{1}−\frac{\mathrm{1}×\mathrm{1}}{\mathrm{3}}=−\frac{\mathrm{4}}{\mathrm{3}} \\ $$$${z}_{\mathrm{1}} =\mathrm{4}−\frac{\mathrm{1}×\left(\mathrm{5}−\mathrm{1}+\mathrm{4}−\mathrm{7}\right)}{\mathrm{3}}=\mathrm{4}−\frac{\mathrm{1}×\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{11}}{\mathrm{3}} \\ $$$${projection}\:{of}\:{point}\:\left(\mathrm{4},−\mathrm{1},\mathrm{3}\right)\:{is}\:\left({x}_{\mathrm{2}} ,{y}_{\mathrm{2}} ,{z}_{\mathrm{2}} \right): \\ $$$${x}_{\mathrm{2}} =\mathrm{4}−\frac{\mathrm{1}×\left(\mathrm{4}−\mathrm{1}+\mathrm{3}−\mathrm{7}\right)}{\mathrm{3}}=\mathrm{4}−\frac{\mathrm{1}×\left(−\mathrm{1}\right)}{\mathrm{3}}=\frac{\mathrm{13}}{\mathrm{3}} \\ $$$${y}_{\mathrm{2}} =−\mathrm{1}−\frac{\mathrm{1}×\left(\mathrm{4}−\mathrm{1}+\mathrm{3}−\mathrm{7}\right)}{\mathrm{3}}=−\mathrm{1}−\frac{\mathrm{1}×\left(−\mathrm{1}\right)}{\mathrm{3}}=−\frac{\mathrm{2}}{\mathrm{3}} \\ $$$${z}_{\mathrm{2}} =\mathrm{3}−\frac{\mathrm{1}×\left(\mathrm{4}−\mathrm{1}+\mathrm{3}−\mathrm{7}\right)}{\mathrm{3}}=\mathrm{3}−\frac{\mathrm{1}×\left(−\mathrm{1}\right)}{\mathrm{3}}=\frac{\mathrm{10}}{\mathrm{3}} \\ $$$${length}\:{of}\:{projection}: \\ $$$${L}=\frac{\mathrm{1}}{\mathrm{3}}\sqrt{\left(\mathrm{14}−\mathrm{13}\right)^{\mathrm{2}} +\left(−\mathrm{4}+\mathrm{2}\right)^{\mathrm{2}} +\left(\mathrm{11}−\mathrm{10}\right)^{\mathrm{2}} }=\sqrt{\frac{\mathrm{2}}{\mathrm{3}}} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 14/Oct/18
distance between (5,−1,4) and (4,−1,3) (√((5−4)^2 +(−1+1)^2 +(4−3)^2 )) =(√2) the st line joining (5,−1,4) and(4,−1,3) ((x−5)/(4−5))=((y+1)/0)=((z−4)/(3−4))=→((x−5)/1)=((y+1)/0)=((z−4)/1) angle between normsl to the plane and the st line cosθ=((1×1+0×1+1×1)/( (√(1^2 +1^2 +1^2 )) ×(√(1^2 +o^2 +1^2 )))) =(2/( (√3) ×(√2) )) sinθ=((√2)/( (√6) )) projection=p sinθ=(p/d) p=dsinθ=(√2) ×((√2)/( (√6)))=((√2)/( (√3)))
$${distance}\:{between}\:\left(\mathrm{5},−\mathrm{1},\mathrm{4}\right)\:{and}\:\left(\mathrm{4},−\mathrm{1},\mathrm{3}\right) \\ $$$$\sqrt{\left(\mathrm{5}−\mathrm{4}\right)^{\mathrm{2}} +\left(−\mathrm{1}+\mathrm{1}\right)^{\mathrm{2}} +\left(\mathrm{4}−\mathrm{3}\right)^{\mathrm{2}} }\:=\sqrt{\mathrm{2}}\: \\ $$$${the}\:{st}\:{line}\:{joining}\:\left(\mathrm{5},−\mathrm{1},\mathrm{4}\right)\:{and}\left(\mathrm{4},−\mathrm{1},\mathrm{3}\right) \\ $$$$\frac{{x}−\mathrm{5}}{\mathrm{4}−\mathrm{5}}=\frac{{y}+\mathrm{1}}{\mathrm{0}}=\frac{{z}−\mathrm{4}}{\mathrm{3}−\mathrm{4}}=\rightarrow\frac{{x}−\mathrm{5}}{\mathrm{1}}=\frac{{y}+\mathrm{1}}{\mathrm{0}}=\frac{{z}−\mathrm{4}}{\mathrm{1}} \\ $$$${angle}\:{between}\:{normsl}\:{to}\:{the}\:{plane}\:{and}\:{the}\:{st} \\ $$$${line}\:{cos}\theta=\frac{\mathrm{1}×\mathrm{1}+\mathrm{0}×\mathrm{1}+\mathrm{1}×\mathrm{1}}{\:\sqrt{\mathrm{1}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} }\:\:×\sqrt{\mathrm{1}^{\mathrm{2}} +{o}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} }}\:=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}\:×\sqrt{\mathrm{2}}\:} \\ $$$${sin}\theta=\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{6}}\:} \\ $$$${projection}={p} \\ $$$${sin}\theta=\frac{{p}}{{d}}\:\:\:{p}={dsin}\theta=\sqrt{\mathrm{2}}\:×\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{6}}}=\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{3}}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *