Menu Close

Question-45638

Tinku Tara 0 Comments
Pin




Question Number 45638 by peter frank last updated on 14/Oct/18
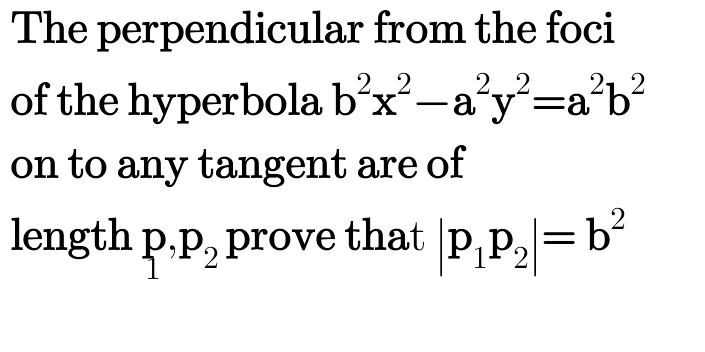
Answered by tanmay.chaudhury50@gmail.com last updated on 15/Oct/18
(x^2 /a^2 )−(y^2 /b^2 )=1 (asecθ,btanθ) lies on hyperbola eqn of tangent at(x_1 ,y_1 ) is ((xx_1 )/a^2 )−((yy_1 )/b^2 )=1 here (x_1 ,y_1 )=(asecθ,btanθ) ((x×asecθ)/a^2 )−((y×btanθ)/b^2 )=1 ((xsecθ)/a)−((ytanθ)/b)=1 the foci of hyperbola are(±(√(a^2 +b^2 )) ,0) xbsecθ−yatanθ−ab=0 distancdfrom((√(a^2 +b^2 )),^� 0) to the above tangent is P_1 and (−(√(a^2 +b^2 )) ,0) isP_2 to prove ∣P_1 P_2 ∣=b^2 P_1 =∣((((√(a^2 +b^2 )) ×bsecθ)−ab)/( (√(b^2 sec^2 θ+a^2 tan^2 θ))))∣ P_2 =∣((−(√(a^2 +b^2 )) ×bsecθ−ab)/( (√(b^2 sec^2 θ+a^2 tan^2 θ))))∣ P_1 P_2 =(((a^2 +b^2 )b^2 sec^2 θ−a^2 b^2 )/(b^2 sec^2 θ+a^2 tan^2 θ)) =b^2 ×(((a^2 +b^2 )sec^2 θ−a^2 )/(b^2 sec^2 θ+a^2 (sec^2 θ−1))) =b^2 ×(((a^2 +b^2 )sec^2 θ−a^2 )/((a^2 +b^2 )sec^2 θ−a^2 ))=b^2 proved ^=
$$\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }−\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1}\:\:\:\left({asec}\theta,{btan}\theta\right)\:{lies}\:{on}\:{hyperbola} \\ $$$${eqn}\:{of}\:{tangent}\:\:{at}\left({x}_{\mathrm{1}} ,{y}_{\mathrm{1}} \right)\:{is} \\ $$$$\frac{{xx}_{\mathrm{1}} }{{a}^{\mathrm{2}} }−\frac{{yy}_{\mathrm{1}} }{{b}^{\mathrm{2}} }=\mathrm{1}\:\:{here}\:\left({x}_{\mathrm{1}} ,{y}_{\mathrm{1}} \right)=\left({asec}\theta,{btan}\theta\right) \\ $$$$\frac{{x}×{asec}\theta}{{a}^{\mathrm{2}} }−\frac{{y}×{btan}\theta}{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\frac{{xsec}\theta}{{a}}−\frac{{ytan}\theta}{{b}}=\mathrm{1} \\ $$$${the}\:{foci}\:{of}\:{hyperbola}\:{are}\left(\pm\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\:,\mathrm{0}\right) \\ $$$${xbsec}\theta−{yatan}\theta−{ab}=\mathrm{0} \\ $$$${distancdfrom}\left(\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\bar {,}\mathrm{0}\right)\:{to}\:{the}\:{above}\:{tangent} \\ $$$${is}\:{P}_{\mathrm{1}} \:{and}\:\left(−\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\:,\mathrm{0}\right)\:{isP}_{\mathrm{2}} \\ $$$${to}\:{prove}\:\mid{P}_{\mathrm{1}} {P}_{\mathrm{2}} \mid={b}^{\mathrm{2}} \\ $$$${P}_{\mathrm{1}} =\mid\frac{\left(\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\:×{bsec}\theta\right)−{ab}}{\:\sqrt{{b}^{\mathrm{2}} {sec}^{\mathrm{2}} \theta+{a}^{\mathrm{2}} {tan}^{\mathrm{2}} \theta}}\mid \\ $$$${P}_{\mathrm{2}} =\mid\frac{−\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\:×{bsec}\theta−{ab}}{\:\sqrt{{b}^{\mathrm{2}} {sec}^{\mathrm{2}} \theta+{a}^{\mathrm{2}} {tan}^{\mathrm{2}} \theta}}\mid \\ $$$${P}_{\mathrm{1}} {P}_{\mathrm{2}} =\frac{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right){b}^{\mathrm{2}} {sec}^{\mathrm{2}} \theta−{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{{b}^{\mathrm{2}} {sec}^{\mathrm{2}} \theta+{a}^{\mathrm{2}} {tan}^{\mathrm{2}} \theta} \\ $$$$\:\:\:={b}^{\mathrm{2}} ×\frac{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right){sec}^{\mathrm{2}} \theta−{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} {sec}^{\mathrm{2}} \theta+{a}^{\mathrm{2}} \left({sec}^{\mathrm{2}} \theta−\mathrm{1}\right)} \\ $$$$\:\:\:\:={b}^{\mathrm{2}} ×\frac{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right){sec}^{\mathrm{2}} \theta−{a}^{\mathrm{2}} }{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right){sec}^{\mathrm{2}} \theta−{a}^{\mathrm{2}} }={b}^{\mathrm{2}} \:\:{proved} \\ $$$$\:\:\:\:\overset{=} {\:} \\ $$$$ \\ $$
Commented by peter frank last updated on 20/Oct/18
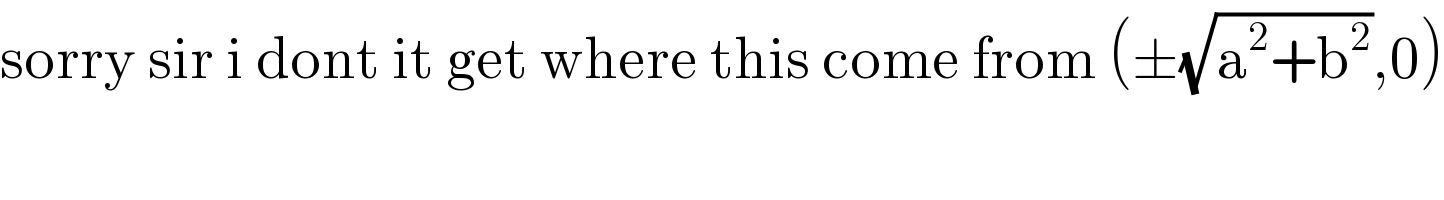
sorry sir i dont it get where this come from (±(√(a^2 +b^2 )),0)
$$\mathrm{sorry}\:\mathrm{sir}\:\mathrm{i}\:\mathrm{dont}\:\mathrm{it}\:\mathrm{get}\:\mathrm{where}\:\mathrm{this}\:\mathrm{come}\:\mathrm{from}\:\left(\pm\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} },\mathrm{0}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *