Question Number 45641 by Necxx last updated on 15/Oct/18

Commented by Necxx last updated on 15/Oct/18
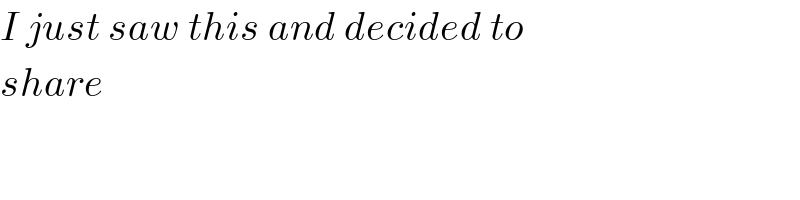
$${I}\:{just}\:{saw}\:{this}\:{and}\:{decided}\:{to} \\ $$$${share} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 15/Oct/18
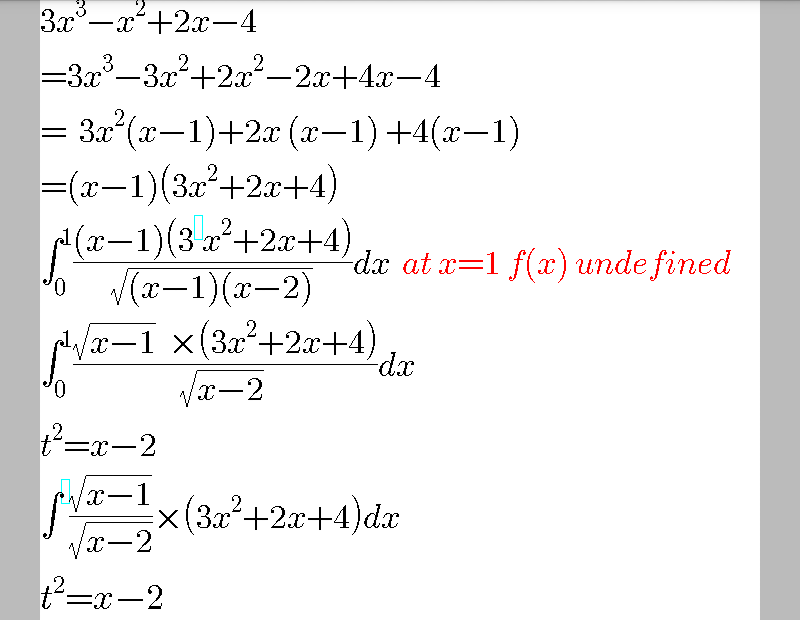
Commented by Necxx last updated on 15/Oct/18
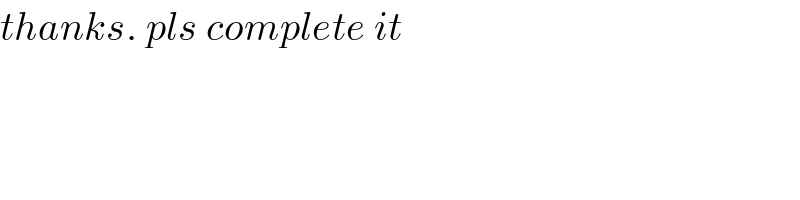
$${thanks}.\:{pls}\:{complete}\:{it} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 15/Oct/18
![3I_1 =(3/5)(t^2 +1)^(5/2) −(t^2 +1)^(3/2) +c_1 14I_2 =14∫t^ (√(t^2 +1)) dt =14∫k×kdk k^2 =t^2 +1 kdk=tdt =14×(k^3 /3)=((14)/3)(t^2 +1)^(3/2) +c_2 20∫((√(t^2 +1))/t)dt =20∫((√(t^2 +1))/t^2 ) ×tdt =20∫((k×kdk)/(k^2 −1)) =20[∫((k^2 −1+1)/(k^2 −1))dk =20[∫dk+(1/2)∫(((k+1)−(k−1))/((k+1)(k−1)))dk] =20[k+(1/2)ln(((k−1)/(k+1)))] =20[(√(t^2 +1)) +(1/2)ln((((√(t^2 +1)) −1)/( (√(t^2 +1)) +1)) )]+c_3 complete ansser 3I_1 +14I_2 +20I_3 (3/5)(t^2 +1)^(5/2) −(t^2 +1)^(3/2) +((14)/3)(t^2 +1)^(3/2) +20(√(t^2 +1)) + 10ln((((√(t^2 +1)) −1)/( (√(t^2 +1)) +1)) ) (3/5)(x−1)^(5/2) +((11)/3)(x−1)^(3/2) +20(√(x−1)) +10ln∣((((√(x−1)) −1)/( (√(x−1)) +1)))∣](https://www.tinkutara.com/question/Q45664.png)
$$\mathrm{3}{I}_{\mathrm{1}} =\frac{\mathrm{3}}{\mathrm{5}}\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\frac{\mathrm{5}}{\mathrm{2}}} −\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} +{c}_{\mathrm{1}} \\ $$$$\mathrm{14}{I}_{\mathrm{2}} =\mathrm{14}\int{t}^{} \sqrt{{t}^{\mathrm{2}} +\mathrm{1}}\:{dt} \\ $$$$=\mathrm{14}\int{k}×{kdk}\:\:\:\:\:\:{k}^{\mathrm{2}} ={t}^{\mathrm{2}} +\mathrm{1}\:\:\:{kdk}={tdt} \\ $$$$=\mathrm{14}×\frac{{k}^{\mathrm{3}} }{\mathrm{3}}=\frac{\mathrm{14}}{\mathrm{3}}\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} +{c}_{\mathrm{2}} \\ $$$$\mathrm{20}\int\frac{\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}}{{t}}{dt} \\ $$$$=\mathrm{20}\int\frac{\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}}{{t}^{\mathrm{2}} }\:×{tdt} \\ $$$$=\mathrm{20}\int\frac{{k}×{kdk}}{{k}^{\mathrm{2}} −\mathrm{1}} \\ $$$$=\mathrm{20}\left[\int\frac{{k}^{\mathrm{2}} −\mathrm{1}+\mathrm{1}}{{k}^{\mathrm{2}} −\mathrm{1}}{dk}\right. \\ $$$$=\mathrm{20}\left[\int{dk}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\left({k}+\mathrm{1}\right)−\left({k}−\mathrm{1}\right)}{\left({k}+\mathrm{1}\right)\left({k}−\mathrm{1}\right)}{dk}\right] \\ $$$$=\mathrm{20}\left[{k}+\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{{k}−\mathrm{1}}{{k}+\mathrm{1}}\right)\right] \\ $$$$=\mathrm{20}\left[\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}\:\:+\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}\:−\mathrm{1}}{\:\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}\:+\mathrm{1}}\:\right)\right]+{c}_{\mathrm{3}} \\ $$$${complete}\:{ansser} \\ $$$$\mathrm{3}{I}_{\mathrm{1}} +\mathrm{14}{I}_{\mathrm{2}} +\mathrm{20}{I}_{\mathrm{3}} \\ $$$$\frac{\mathrm{3}}{\mathrm{5}}\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\frac{\mathrm{5}}{\mathrm{2}}} −\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} +\frac{\mathrm{14}}{\mathrm{3}}\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} +\mathrm{20}\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}\:+ \\ $$$$\:\:\mathrm{10}{ln}\left(\frac{\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}\:−\mathrm{1}}{\:\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}\:+\mathrm{1}}\:\right) \\ $$$$\frac{\mathrm{3}}{\mathrm{5}}\left({x}−\mathrm{1}\right)^{\frac{\mathrm{5}}{\mathrm{2}}} +\frac{\mathrm{11}}{\mathrm{3}}\left({x}−\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} +\mathrm{20}\sqrt{{x}−\mathrm{1}}\:+\mathrm{10}{ln}\mid\left(\frac{\sqrt{{x}−\mathrm{1}}\:−\mathrm{1}}{\:\sqrt{{x}−\mathrm{1}}\:+\mathrm{1}}\right)\mid \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 15/Oct/18

Commented by tanmay.chaudhury50@gmail.com last updated on 15/Oct/18

Commented by tanmay.chaudhury50@gmail.com last updated on 15/Oct/18
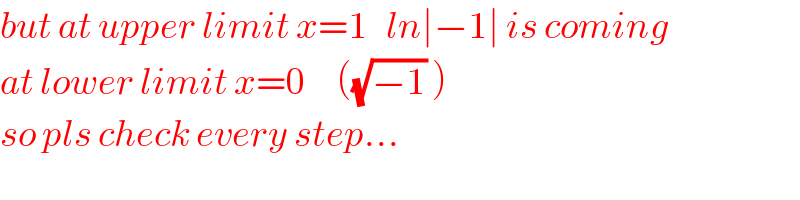
$${but}\:{at}\:{upper}\:{limit}\:{x}=\mathrm{1}\:\:\:{ln}\mid−\mathrm{1}\mid\:{is}\:{coming} \\ $$$${at}\:{lower}\:{limit}\:{x}=\mathrm{0}\:\:\:\:\:\left(\sqrt{−\mathrm{1}}\:\right) \\ $$$${so}\:{pls}\:{check}\:{every}\:{step}… \\ $$
Commented by Necxx last updated on 15/Oct/18
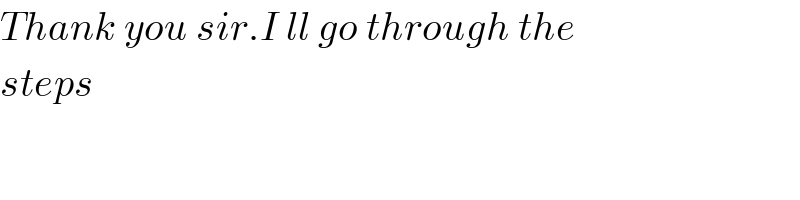
$${Thank}\:{you}\:{sir}.{I}\:{ll}\:{go}\:{through}\:{the} \\ $$$${steps} \\ $$
Answered by Meritguide1234 last updated on 15/Oct/18

