Menu Close

Question-45673

Tinku Tara 0 Comments
Pin




Question Number 45673 by ajfour last updated on 15/Oct/18
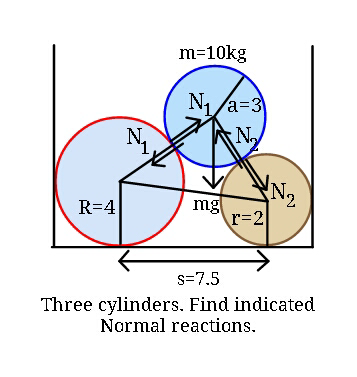
Commented by ajfour last updated on 15/Oct/18
Assuming no friction anywhere, find N_1 , N_2 .
$${Assuming}\:{no}\:{friction}\:{anywhere}, \\ $$$${find}\:{N}_{\mathrm{1}} ,\:{N}_{\mathrm{2}} \:. \\ $$
Answered by MrW3 last updated on 15/Oct/18
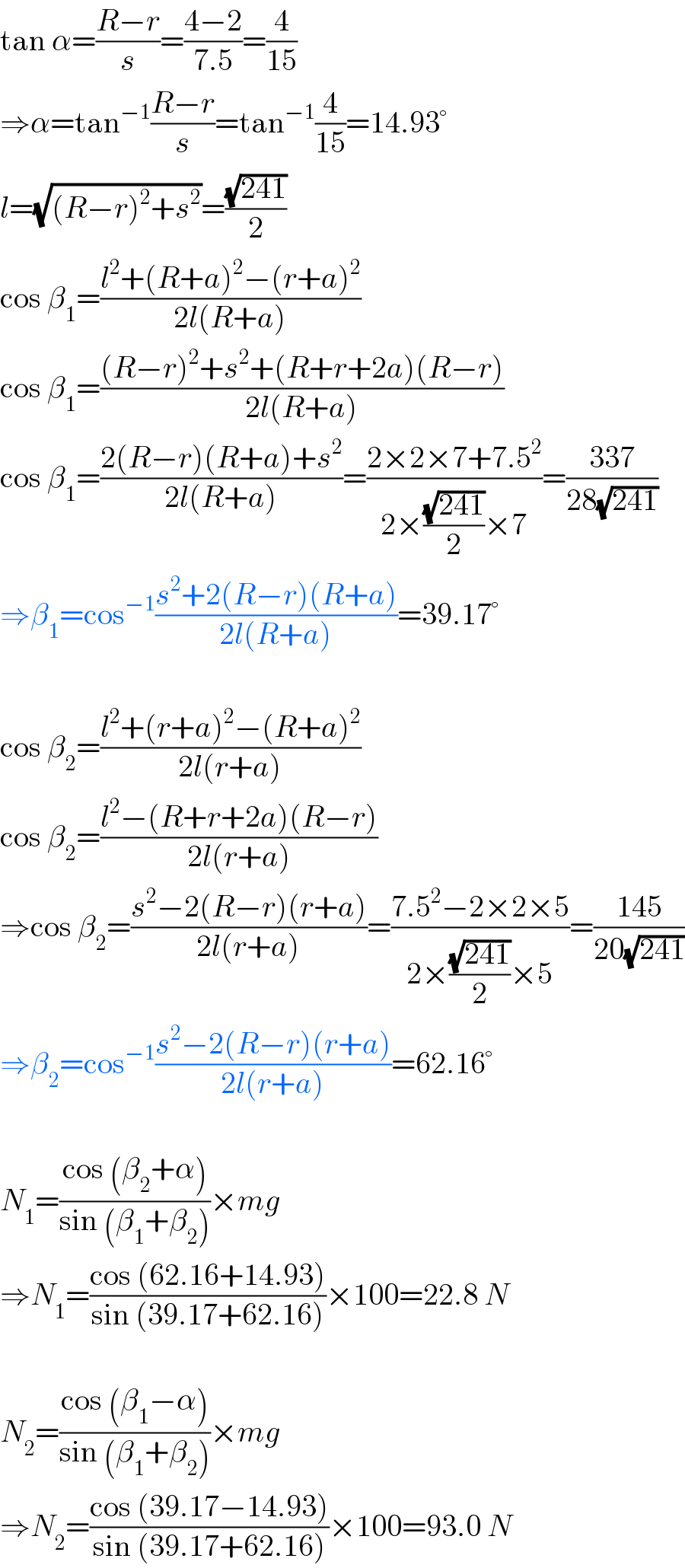
tan α=((R−r)/s)=((4−2)/(7.5))=(4/(15)) ⇒α=tan^(−1) ((R−r)/s)=tan^(−1) (4/(15))=14.93° l=(√((R−r)^2 +s^2 ))=((√(241))/2) cos β_1 =((l^2 +(R+a)^2 −(r+a)^2 )/(2l(R+a))) cos β_1 =(((R−r)^2 +s^2 +(R+r+2a)(R−r))/(2l(R+a))) cos β_1 =((2(R−r)(R+a)+s^2 )/(2l(R+a)))=((2×2×7+7.5^2 )/(2×((√(241))/2)×7))=((337)/(28(√(241)))) ⇒β_1 =cos^(−1) ((s^2 +2(R−r)(R+a))/(2l(R+a)))=39.17° cos β_2 =((l^2 +(r+a)^2 −(R+a)^2 )/(2l(r+a))) cos β_2 =((l^2 −(R+r+2a)(R−r))/(2l(r+a))) ⇒cos β_2 =((s^2 −2(R−r)(r+a))/(2l(r+a)))=((7.5^2 −2×2×5)/(2×((√(241))/2)×5))=((145)/(20(√(241)))) ⇒β_2 =cos^(−1) ((s^2 −2(R−r)(r+a))/(2l(r+a)))=62.16° N_1 =((cos (β_2 +α))/(sin (β_1 +β_2 )))×mg ⇒N_1 =((cos (62.16+14.93))/(sin (39.17+62.16)))×100=22.8 N N_2 =((cos (β_1 −α))/(sin (β_1 +β_2 )))×mg ⇒N_2 =((cos (39.17−14.93))/(sin (39.17+62.16)))×100=93.0 N
$$\mathrm{tan}\:\alpha=\frac{{R}−{r}}{{s}}=\frac{\mathrm{4}−\mathrm{2}}{\mathrm{7}.\mathrm{5}}=\frac{\mathrm{4}}{\mathrm{15}} \\ $$$$\Rightarrow\alpha=\mathrm{tan}^{−\mathrm{1}} \frac{{R}−{r}}{{s}}=\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{4}}{\mathrm{15}}=\mathrm{14}.\mathrm{93}° \\ $$$${l}=\sqrt{\left({R}−{r}\right)^{\mathrm{2}} +{s}^{\mathrm{2}} }=\frac{\sqrt{\mathrm{241}}}{\mathrm{2}} \\ $$$$\mathrm{cos}\:\beta_{\mathrm{1}} =\frac{{l}^{\mathrm{2}} +\left({R}+{a}\right)^{\mathrm{2}} −\left({r}+{a}\right)^{\mathrm{2}} }{\mathrm{2}{l}\left({R}+{a}\right)} \\ $$$$\mathrm{cos}\:\beta_{\mathrm{1}} =\frac{\left({R}−{r}\right)^{\mathrm{2}} +{s}^{\mathrm{2}} +\left({R}+{r}+\mathrm{2}{a}\right)\left({R}−{r}\right)}{\mathrm{2}{l}\left({R}+{a}\right)} \\ $$$$\mathrm{cos}\:\beta_{\mathrm{1}} =\frac{\mathrm{2}\left({R}−{r}\right)\left({R}+{a}\right)+{s}^{\mathrm{2}} }{\mathrm{2}{l}\left({R}+{a}\right)}=\frac{\mathrm{2}×\mathrm{2}×\mathrm{7}+\mathrm{7}.\mathrm{5}^{\mathrm{2}} }{\mathrm{2}×\frac{\sqrt{\mathrm{241}}}{\mathrm{2}}×\mathrm{7}}=\frac{\mathrm{337}}{\mathrm{28}\sqrt{\mathrm{241}}} \\ $$$$\Rightarrow\beta_{\mathrm{1}} =\mathrm{cos}^{−\mathrm{1}} \frac{{s}^{\mathrm{2}} +\mathrm{2}\left({R}−{r}\right)\left({R}+{a}\right)}{\mathrm{2}{l}\left({R}+{a}\right)}=\mathrm{39}.\mathrm{17}° \\ $$$$ \\ $$$$\mathrm{cos}\:\beta_{\mathrm{2}} =\frac{{l}^{\mathrm{2}} +\left({r}+{a}\right)^{\mathrm{2}} −\left({R}+{a}\right)^{\mathrm{2}} }{\mathrm{2}{l}\left({r}+{a}\right)} \\ $$$$\mathrm{cos}\:\beta_{\mathrm{2}} =\frac{{l}^{\mathrm{2}} −\left({R}+{r}+\mathrm{2}{a}\right)\left({R}−{r}\right)}{\mathrm{2}{l}\left({r}+{a}\right)} \\ $$$$\Rightarrow\mathrm{cos}\:\beta_{\mathrm{2}} =\frac{{s}^{\mathrm{2}} −\mathrm{2}\left({R}−{r}\right)\left({r}+{a}\right)}{\mathrm{2}{l}\left({r}+{a}\right)}=\frac{\mathrm{7}.\mathrm{5}^{\mathrm{2}} −\mathrm{2}×\mathrm{2}×\mathrm{5}}{\mathrm{2}×\frac{\sqrt{\mathrm{241}}}{\mathrm{2}}×\mathrm{5}}=\frac{\mathrm{145}}{\mathrm{20}\sqrt{\mathrm{241}}} \\ $$$$\Rightarrow\beta_{\mathrm{2}} =\mathrm{cos}^{−\mathrm{1}} \frac{{s}^{\mathrm{2}} −\mathrm{2}\left({R}−{r}\right)\left({r}+{a}\right)}{\mathrm{2}{l}\left({r}+{a}\right)}=\mathrm{62}.\mathrm{16}° \\ $$$$ \\ $$$${N}_{\mathrm{1}} =\frac{\mathrm{cos}\:\left(\beta_{\mathrm{2}} +\alpha\right)}{\mathrm{sin}\:\left(\beta_{\mathrm{1}} +\beta_{\mathrm{2}} \right)}×{mg} \\ $$$$\Rightarrow{N}_{\mathrm{1}} =\frac{\mathrm{cos}\:\left(\mathrm{62}.\mathrm{16}+\mathrm{14}.\mathrm{93}\right)}{\mathrm{sin}\:\left(\mathrm{39}.\mathrm{17}+\mathrm{62}.\mathrm{16}\right)}×\mathrm{100}=\mathrm{22}.\mathrm{8}\:{N} \\ $$$$ \\ $$$${N}_{\mathrm{2}} =\frac{\mathrm{cos}\:\left(\beta_{\mathrm{1}} −\alpha\right)}{\mathrm{sin}\:\left(\beta_{\mathrm{1}} +\beta_{\mathrm{2}} \right)}×{mg} \\ $$$$\Rightarrow{N}_{\mathrm{2}} =\frac{\mathrm{cos}\:\left(\mathrm{39}.\mathrm{17}−\mathrm{14}.\mathrm{93}\right)}{\mathrm{sin}\:\left(\mathrm{39}.\mathrm{17}+\mathrm{62}.\mathrm{16}\right)}×\mathrm{100}=\mathrm{93}.\mathrm{0}\:{N} \\ $$
Commented by MrW3 last updated on 15/Oct/18
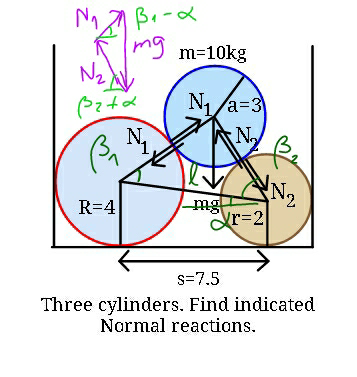
Commented by ajfour last updated on 15/Oct/18
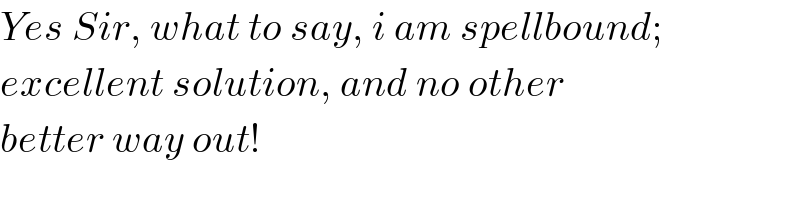
Yes Sir, what to say, i am spellbound; excellent solution, and no other better way out!
$${Yes}\:{Sir},\:{what}\:{to}\:{say},\:{i}\:{am}\:{spellbound}; \\ $$$${excellent}\:{solution},\:{and}\:{no}\:{other} \\ $$$${better}\:{way}\:{out}! \\ $$
Commented by behi83417@gmail.com last updated on 15/Oct/18
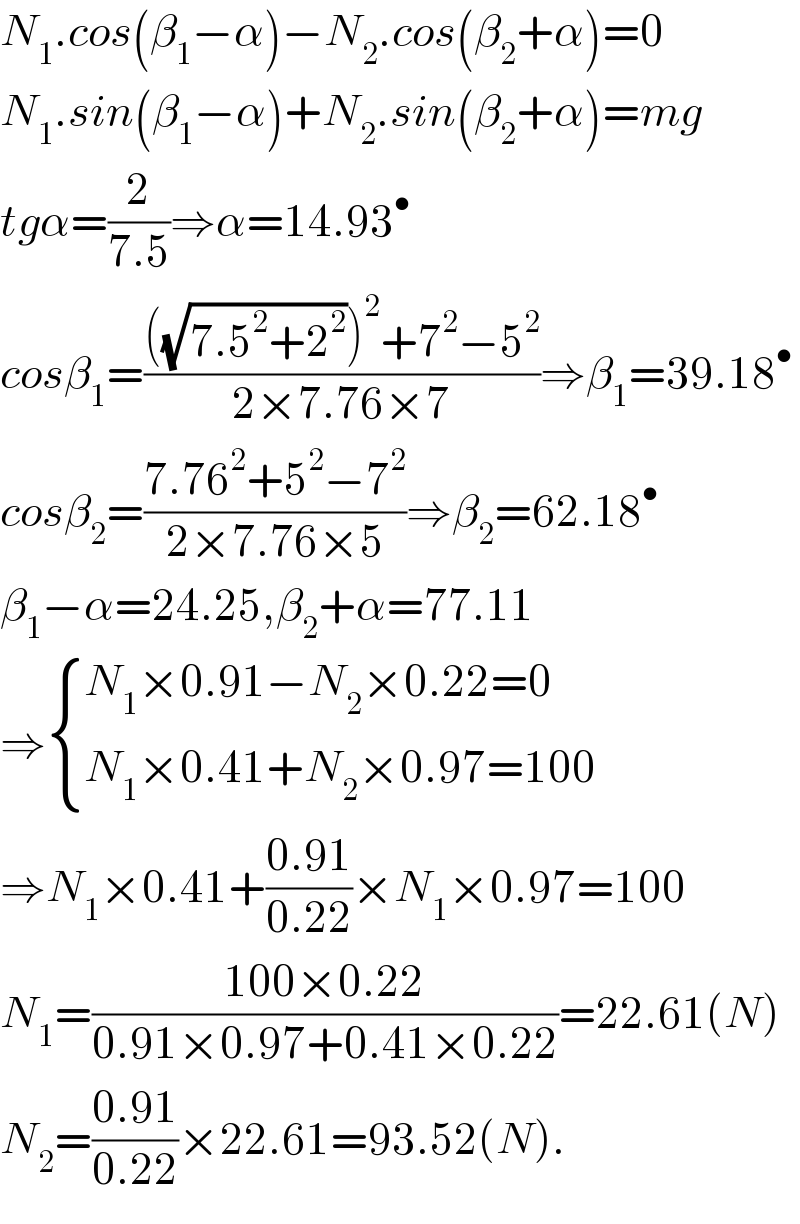
N_1 .cos(β_1 −α)−N_2 .cos(β_2 +α)=0 N_1 .sin(β_1 −α)+N_2 .sin(β_2 +α)=mg tgα=(2/(7.5))⇒α=14.93^• cosβ_1 =((((√(7.5^2 +2^2 )))^2 +7^2 −5^2 )/(2×7.76×7))⇒β_1 =39.18^• cosβ_2 =((7.76^2 +5^2 −7^2 )/(2×7.76×5))⇒β_2 =62.18^• β_1 −α=24.25,β_2 +α=77.11 ⇒ { ((N_1 ×0.91−N_2 ×0.22=0)),((N_1 ×0.41+N_2 ×0.97=100)) :} ⇒N_1 ×0.41+((0.91)/(0.22))×N_1 ×0.97=100 N_1 =((100×0.22)/(0.91×0.97+0.41×0.22))=22.61(N) N_2 =((0.91)/(0.22))×22.61=93.52(N).
$${N}_{\mathrm{1}} .{cos}\left(\beta_{\mathrm{1}} −\alpha\right)−{N}_{\mathrm{2}} .{cos}\left(\beta_{\mathrm{2}} +\alpha\right)=\mathrm{0} \\ $$$${N}_{\mathrm{1}} .{sin}\left(\beta_{\mathrm{1}} −\alpha\right)+{N}_{\mathrm{2}} .{sin}\left(\beta_{\mathrm{2}} +\alpha\right)={mg} \\ $$$${tg}\alpha=\frac{\mathrm{2}}{\mathrm{7}.\mathrm{5}}\Rightarrow\alpha=\mathrm{14}.\mathrm{93}^{\bullet} \\ $$$${cos}\beta_{\mathrm{1}} =\frac{\left(\sqrt{\mathrm{7}.\mathrm{5}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} }\right)^{\mathrm{2}} +\mathrm{7}^{\mathrm{2}} −\mathrm{5}^{\mathrm{2}} }{\mathrm{2}×\mathrm{7}.\mathrm{76}×\mathrm{7}}\Rightarrow\beta_{\mathrm{1}} =\mathrm{39}.\mathrm{18}^{\bullet} \\ $$$${cos}\beta_{\mathrm{2}} =\frac{\mathrm{7}.\mathrm{76}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} −\mathrm{7}^{\mathrm{2}} }{\mathrm{2}×\mathrm{7}.\mathrm{76}×\mathrm{5}}\Rightarrow\beta_{\mathrm{2}} =\mathrm{62}.\mathrm{18}^{\bullet} \\ $$$$\beta_{\mathrm{1}} −\alpha=\mathrm{24}.\mathrm{25},\beta_{\mathrm{2}} +\alpha=\mathrm{77}.\mathrm{11} \\ $$$$\Rightarrow\begin{cases}{{N}_{\mathrm{1}} ×\mathrm{0}.\mathrm{91}−{N}_{\mathrm{2}} ×\mathrm{0}.\mathrm{22}=\mathrm{0}}\\{{N}_{\mathrm{1}} ×\mathrm{0}.\mathrm{41}+{N}_{\mathrm{2}} ×\mathrm{0}.\mathrm{97}=\mathrm{100}}\end{cases} \\ $$$$\Rightarrow{N}_{\mathrm{1}} ×\mathrm{0}.\mathrm{41}+\frac{\mathrm{0}.\mathrm{91}}{\mathrm{0}.\mathrm{22}}×{N}_{\mathrm{1}} ×\mathrm{0}.\mathrm{97}=\mathrm{100} \\ $$$${N}_{\mathrm{1}} =\frac{\mathrm{100}×\mathrm{0}.\mathrm{22}}{\mathrm{0}.\mathrm{91}×\mathrm{0}.\mathrm{97}+\mathrm{0}.\mathrm{41}×\mathrm{0}.\mathrm{22}}=\mathrm{22}.\mathrm{61}\left({N}\right) \\ $$$${N}_{\mathrm{2}} =\frac{\mathrm{0}.\mathrm{91}}{\mathrm{0}.\mathrm{22}}×\mathrm{22}.\mathrm{61}=\mathrm{93}.\mathrm{52}\left({N}\right). \\ $$
Commented by MrW3 last updated on 15/Oct/18
thank you sir!
$${thank}\:{you}\:{sir}! \\ $$
Commented by behi83417@gmail.com last updated on 16/Oct/18
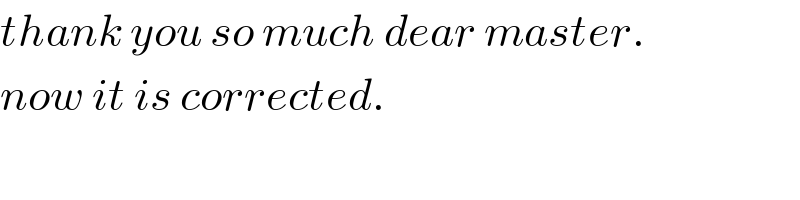
thank you so much dear master. now it is corrected.
$${thank}\:{you}\:{so}\:{much}\:{dear}\:{master}. \\ $$$${now}\:{it}\:{is}\:{corrected}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *