Menu Close

Question-45690

Tinku Tara 0 Comments
Pin




Question Number 45690 by ajfour last updated on 15/Oct/18
Commented by ajfour last updated on 15/Oct/18
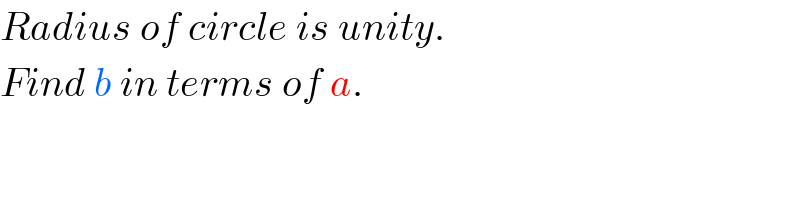
Radius of circle is unity. Find b in terms of a.
$${Radius}\:{of}\:{circle}\:{is}\:{unity}. \\ $$$${Find}\:{b}\:{in}\:{terms}\:{of}\:{a}. \\ $$
Answered by MrW3 last updated on 15/Oct/18
Commented by ajfour last updated on 15/Oct/18
Thank you so much Sir; it is indeed a matter of faith. BEAUTIFUL !
$${Thank}\:{you}\:{so}\:{much}\:{Sir};\:{it}\:{is} \\ $$$${indeed}\:{a}\:{matter}\:{of}\:{faith}. \\ $$$$\mathcal{BEAUTIFUL}\:! \\ $$
Commented by MrW3 last updated on 15/Oct/18
thank you too sir!
$${thank}\:{you}\:{too}\:{sir}! \\ $$
Commented by MrW3 last updated on 15/Oct/18
tan α=((√((2R)^2 −a^2 ))/a)=((√(4R^2 −a^2 ))/a) γ=2α PT=R tan γ=R tan (2α)=R((2(√(4R^2 −a^2 )))/(a(1−((4R^2 −a^2 )/a^2 ))))=((aR(√(4R^2 −a^2 )))/(a^2 −2R^2 )) tan β=((PT)/(2R))=((a(√(4R^2 −a^2 )))/(2(a^2 −2R^2 ))) cos β=((2(a^2 −2R^2 ))/( (√(a^2 (4R^2 −a^2 )+4(a^2 −2R^2 )^2 )))) cos β=((2(a^2 −2R^2 ))/( (√(3a^4 +16R^4 −12a^2 R^2 )))) cos β=((2(a^2 −2R^2 ))/( (√(3(a^2 −2R^2 )^2 +4R^4 )))) b=2R cos β ⇒b=((4R(a^2 −2R^2 ))/( (√(3(a^2 −2R^2 )^2 +4R^4 )))) for R=1: ⇒b=((4(a^2 −2))/( (√(3(a^2 −2)^2 +4))))
$$\mathrm{tan}\:\alpha=\frac{\sqrt{\left(\mathrm{2}{R}\right)^{\mathrm{2}} −{a}^{\mathrm{2}} }}{{a}}=\frac{\sqrt{\mathrm{4}{R}^{\mathrm{2}} −{a}^{\mathrm{2}} }}{{a}} \\ $$$$\gamma=\mathrm{2}\alpha \\ $$$${PT}={R}\:\mathrm{tan}\:\gamma={R}\:\mathrm{tan}\:\left(\mathrm{2}\alpha\right)={R}\frac{\mathrm{2}\sqrt{\mathrm{4}{R}^{\mathrm{2}} −{a}^{\mathrm{2}} }}{{a}\left(\mathrm{1}−\frac{\mathrm{4}{R}^{\mathrm{2}} −{a}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right)}=\frac{{aR}\sqrt{\mathrm{4}{R}^{\mathrm{2}} −{a}^{\mathrm{2}} }}{{a}^{\mathrm{2}} −\mathrm{2}{R}^{\mathrm{2}} } \\ $$$$\mathrm{tan}\:\beta=\frac{{PT}}{\mathrm{2}{R}}=\frac{{a}\sqrt{\mathrm{4}{R}^{\mathrm{2}} −{a}^{\mathrm{2}} }}{\mathrm{2}\left({a}^{\mathrm{2}} −\mathrm{2}{R}^{\mathrm{2}} \right)} \\ $$$$\mathrm{cos}\:\beta=\frac{\mathrm{2}\left({a}^{\mathrm{2}} −\mathrm{2}{R}^{\mathrm{2}} \right)}{\:\sqrt{{a}^{\mathrm{2}} \left(\mathrm{4}{R}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)+\mathrm{4}\left({a}^{\mathrm{2}} −\mathrm{2}{R}^{\mathrm{2}} \right)^{\mathrm{2}} }} \\ $$$$\mathrm{cos}\:\beta=\frac{\mathrm{2}\left({a}^{\mathrm{2}} −\mathrm{2}{R}^{\mathrm{2}} \right)}{\:\sqrt{\mathrm{3}{a}^{\mathrm{4}} +\mathrm{16}{R}^{\mathrm{4}} −\mathrm{12}{a}^{\mathrm{2}} {R}^{\mathrm{2}} }} \\ $$$$\mathrm{cos}\:\beta=\frac{\mathrm{2}\left({a}^{\mathrm{2}} −\mathrm{2}{R}^{\mathrm{2}} \right)}{\:\sqrt{\mathrm{3}\left({a}^{\mathrm{2}} −\mathrm{2}{R}^{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{4}{R}^{\mathrm{4}} }} \\ $$$${b}=\mathrm{2}{R}\:\mathrm{cos}\:\beta \\ $$$$\Rightarrow{b}=\frac{\mathrm{4}{R}\left({a}^{\mathrm{2}} −\mathrm{2}{R}^{\mathrm{2}} \right)}{\:\sqrt{\mathrm{3}\left({a}^{\mathrm{2}} −\mathrm{2}{R}^{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{4}{R}^{\mathrm{4}} }} \\ $$$${for}\:{R}=\mathrm{1}: \\ $$$$\Rightarrow{b}=\frac{\mathrm{4}\left({a}^{\mathrm{2}} −\mathrm{2}\right)}{\:\sqrt{\mathrm{3}\left({a}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} +\mathrm{4}}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *