Question Number 45809 by rahul 19 last updated on 17/Oct/18

Commented by rahul 19 last updated on 17/Oct/18
$${Calculation}\:{error}…. \\ $$
Commented by MJS last updated on 17/Oct/18
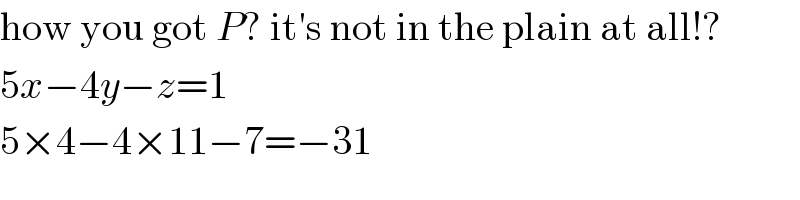
$$\mathrm{how}\:\mathrm{you}\:\mathrm{got}\:{P}?\:\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{in}\:\mathrm{the}\:\mathrm{plain}\:\mathrm{at}\:\mathrm{all}!? \\ $$$$\mathrm{5}{x}−\mathrm{4}{y}−{z}=\mathrm{1} \\ $$$$\mathrm{5}×\mathrm{4}−\mathrm{4}×\mathrm{11}−\mathrm{7}=−\mathrm{31} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 17/Oct/18

$${The}\:{eqn}\:{of}\:{st}\:{line}\:{QR}\:{is} \\ $$$$\frac{{x}−\mathrm{2}}{\mathrm{1}−\mathrm{2}}=\frac{{y}−\mathrm{3}}{−\mathrm{1}−\mathrm{3}}=\frac{{z}−\mathrm{5}}{\mathrm{4}−\mathrm{5}} \\ $$$$\frac{{x}−\mathrm{2}}{\mathrm{1}}=\frac{{y}−\mathrm{3}}{\mathrm{4}}=\frac{{z}−\mathrm{5}}{\mathrm{1}}={r} \\ $$$$\left({r}+\mathrm{2},\mathrm{4}{r}+\mathrm{3},{r}+\mathrm{5}\right)\:{is}\:{the}\:{point}\:{P}…{interdection} \\ $$$${of}\:{st}\:{line}\:{and}\:{plane}… \\ $$$$\mathrm{5}\left({r}+\mathrm{2}\right)−\mathrm{4}\left(\mathrm{4}{r}+\mathrm{3}\right)−\mathrm{1}\left({r}+\mathrm{5}\right)=\mathrm{1} \\ $$$$\mathrm{5}{r}+\mathrm{10}−\mathrm{16}{r}−\mathrm{12}−{r}−\mathrm{5}−\mathrm{1}=\mathrm{0} \\ $$$$−\mathrm{12}{r}−\mathrm{8}=\mathrm{0}\:\:\:{r}=\frac{−\mathrm{2}}{\mathrm{3}} \\ $$$$ \\ $$$${point}\:{P}\left(\frac{−\mathrm{2}}{\mathrm{3}}+\mathrm{2}\:\:,\frac{−\mathrm{8}}{\mathrm{3}}+\mathrm{3}\:\:,\frac{−\mathrm{2}}{\mathrm{3}}+\mathrm{5}\right) \\ $$$$\:\:\:{point}\:{P}\left(\frac{\mathrm{4}}{\mathrm{3}},\frac{\mathrm{1}}{\mathrm{3}},\frac{\mathrm{13}}{\mathrm{3}}\right) \\ $$$${let}\:{point}\:{S}\left(\alpha,\beta,\gamma\right) \\ $$$${poinS}\:{lies}\:{on}\:{QR}\:{so}\:\:\frac{\alpha−\mathrm{2}}{\mathrm{1}}=\frac{\beta−\mathrm{3}}{\mathrm{4}}=\frac{\gamma−\mathrm{5}}{\mathrm{1}}={k} \\ $$$$\left(\alpha,\beta,\gamma\right)=\left({k}+\mathrm{2},\mathrm{4}{k}+\mathrm{3},{k}+\mathrm{5}\right) \\ $$$${direction}\:{ratio}\:{of}\:{TS}\:{that}\:{means}\:{betwedn} \\ $$$$\left({k}+\mathrm{2},\mathrm{4}{k}+\mathrm{3},{k}+\mathrm{5}\right){and}\:\left(\mathrm{2},\mathrm{1},\mathrm{4}\right)\:{is} \\ $$$$\left({k},\mathrm{4}{k}+\mathrm{2},{k}+\mathrm{1}\right) \\ $$$${TS}\bot{QR}\:{atS}\:{so} \\ $$$$\mathrm{1}\left({k}\right)+\mathrm{4}\left(\mathrm{4}{k}+\mathrm{2}\right)+\mathrm{1}\left({k}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\mathrm{18}{k}+\mathrm{8}+\mathrm{1}=\mathrm{0} \\ $$$${k}=\frac{−\mathrm{1}}{\mathrm{2}}\: \\ $$$${so}\:{point}\:{S}\:{is}\left\{\frac{−\mathrm{1}}{\mathrm{2}}+\mathrm{2},\mathrm{4}\left(\frac{−\mathrm{1}}{\mathrm{2}}\right)+\mathrm{3},\frac{−\mathrm{1}}{\mathrm{2}}+\mathrm{5}\right\} \\ $$$$=\left\{\frac{\mathrm{3}}{\mathrm{2}},\mathrm{1},\frac{\mathrm{9}}{\mathrm{2}}\right\}\leftarrow{it}\:{is}\:{point}\:{S} \\ $$$$\left\{\frac{\mathrm{4}}{\mathrm{3}},\frac{\mathrm{1}}{\mathrm{3}},\frac{\mathrm{13}}{\mathrm{3}}\right\}\leftarrow{it}\:{is}\:{point}\:{P} \\ $$$${PS}=\sqrt{\left(\frac{\mathrm{4}}{\mathrm{3}}−\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{1}\right)^{\mathrm{2}} +\left(\frac{\mathrm{13}}{\mathrm{3}}−\frac{\mathrm{9}}{\mathrm{2}}\right)^{\mathrm{2}} }\: \\ $$$$=\sqrt{\left(\frac{−\mathrm{1}}{\mathrm{6}}\right)^{\mathrm{2}} +\left(\frac{−\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{2}} +\left(\frac{−\mathrm{1}}{\mathrm{6}}\right)^{\mathrm{2}} }\: \\ $$$$=\sqrt{\frac{\mathrm{1}}{\mathrm{36}}+\frac{\mathrm{4}}{\mathrm{9}}+\frac{\mathrm{1}}{\mathrm{36}}}\: \\ $$$$=\sqrt{\frac{\mathrm{1}+\mathrm{16}+\mathrm{1}}{\mathrm{36}}}\:=\sqrt{\frac{\mathrm{18}}{\mathrm{36}}}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\:}{ans} \\ $$$$ \\ $$
Commented by rahul 19 last updated on 17/Oct/18
thanks sir!��☺️
Answered by MJS last updated on 17/Oct/18
![line QR=l_1 : X=Q+t(R−Q) l_1 : ((x),(y),(z) ) = ((2),(3),(5) ) −t ((1),(4),(1) ) plane p_1 : 5x−4y−z=1 P=l_1 ∩p_1 5(2−t)−4(3−4t)−(5−t)=1 t=(2/3) ⇒ P= (((4/3)),((1/3)),(((13)/3)) ) plane⊥l_1 =p_2 : x+4y+z=c [the direction of l_1 is the perpendicular of p_2 ] T∈p_2 ⇒ c=10 p_2 : x+4y+z=10 S=l_1 ∩p_2 (2−t)+4(3−4t)+(5−t)=10 t=(1/2) ⇒ S= (((3/2)),(1),((9/2)) ) ∣PS∣=(√(((3/2)−(4/3))^2 +(1−(1/3))^2 +((9/2)−((13)/3))^2 ))=((√2)/2)](https://www.tinkutara.com/question/Q45822.png)
$$\mathrm{line}\:{QR}={l}_{\mathrm{1}} :\:{X}={Q}+{t}\left({R}−{Q}\right) \\ $$$${l}_{\mathrm{1}} :\:\begin{pmatrix}{{x}}\\{{y}}\\{{z}}\end{pmatrix}\:=\begin{pmatrix}{\mathrm{2}}\\{\mathrm{3}}\\{\mathrm{5}}\end{pmatrix}\:−{t}\begin{pmatrix}{\mathrm{1}}\\{\mathrm{4}}\\{\mathrm{1}}\end{pmatrix} \\ $$$$\mathrm{plane}\:{p}_{\mathrm{1}} :\:\mathrm{5}{x}−\mathrm{4}{y}−{z}=\mathrm{1} \\ $$$${P}={l}_{\mathrm{1}} \cap{p}_{\mathrm{1}} \\ $$$$\mathrm{5}\left(\mathrm{2}−{t}\right)−\mathrm{4}\left(\mathrm{3}−\mathrm{4}{t}\right)−\left(\mathrm{5}−{t}\right)=\mathrm{1} \\ $$$${t}=\frac{\mathrm{2}}{\mathrm{3}}\:\Rightarrow\:{P}=\begin{pmatrix}{\frac{\mathrm{4}}{\mathrm{3}}}\\{\frac{\mathrm{1}}{\mathrm{3}}}\\{\frac{\mathrm{13}}{\mathrm{3}}}\end{pmatrix} \\ $$$$\mathrm{plane}\bot{l}_{\mathrm{1}} ={p}_{\mathrm{2}} :\:{x}+\mathrm{4}{y}+{z}={c} \\ $$$$\:\:\:\:\:\left[\mathrm{the}\:\mathrm{direction}\:\mathrm{of}\:{l}_{\mathrm{1}} \:\mathrm{is}\:\mathrm{the}\:\mathrm{perpendicular}\:\mathrm{of}\:{p}_{\mathrm{2}} \right] \\ $$$${T}\in{p}_{\mathrm{2}} \:\Rightarrow\:{c}=\mathrm{10} \\ $$$${p}_{\mathrm{2}} :\:{x}+\mathrm{4}{y}+{z}=\mathrm{10} \\ $$$${S}={l}_{\mathrm{1}} \cap{p}_{\mathrm{2}} \\ $$$$\left(\mathrm{2}−{t}\right)+\mathrm{4}\left(\mathrm{3}−\mathrm{4}{t}\right)+\left(\mathrm{5}−{t}\right)=\mathrm{10} \\ $$$${t}=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\:{S}=\begin{pmatrix}{\frac{\mathrm{3}}{\mathrm{2}}}\\{\mathrm{1}}\\{\frac{\mathrm{9}}{\mathrm{2}}}\end{pmatrix} \\ $$$$\mid{PS}\mid=\sqrt{\left(\frac{\mathrm{3}}{\mathrm{2}}−\frac{\mathrm{4}}{\mathrm{3}}\right)^{\mathrm{2}} +\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{9}}{\mathrm{2}}−\frac{\mathrm{13}}{\mathrm{3}}\right)^{\mathrm{2}} }=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$
Commented by rahul 19 last updated on 17/Oct/18
thanks sir!��☺️
Commented by MJS last updated on 17/Oct/18

$$\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$
